Chapter 14: Evaluating and Improving Theory Using Conceptual Loops—A Science of Conceptual Systems (SOCS) Approach
Wallis, S. E. (2020). Evaluating and improving theory using conceptual loops: A science of conceptual systems (SOCS) approach. Cybernetics and Human Knowing, 27(3).
My thanks go out to two anonymous reviewers; their carefully considered comments and detailed feedback served to generate a more complete and coherent paper.
Abstract
In the field of cybernetics, it is generally accepted that a better theory is one that presents more conceptual loops (often represented diagrammatically with boxes and arrows) which may represent processes in the world of physical, biological, and social systems. However, that assumption has not been adequately tested. This preliminary study evaluates loops and other conceptual structures found in theories drawn from two disciplines, and stages of evolution within those disciplines, that show theories evolving over time from lesser to greater usefulness. Comparing the loop structures with the usefulness of the theories, this paper provides recommendations for measuring the structure of theories as tools for developing theories that are more useful in practical application. Because theories are ubiquitous across academic disciplines and fields of practice, this research is expected to support multi/inter/trans-disciplinary scholars and practitioners.
Introduction
The purpose of this paper is to conduct and present a preliminary exploration of causal loop structures (conceptual loops, or more simply, loops) found within some theories with an eye to developing a method for using loops as one indicator for the quality (effectiveness or usefulness) of theories. That measure, in turn, is expected to suggest one or more directions for accelerating the advance of theories in all sciences, with a particular focus here on improving theories of the social/behavioral sciences. Such advance is expected to provide improvements in practice for the benefit of humans and humanity. Such an approach is called for because present theories have proved insufficient for understanding and resolving the vast problems facing our peoples and our planet.
Theory may be understood as a representation of knowledge, potentially understood as “knowledge_of” or “knowledge_for” (Glanville, 2009). As such, this paper responds to Glanville’s call to explore similarities and differences between the two by exploring how less useful knowledge (knowledge_of) may have fewer loops than knowledge which is of greater use for understanding situations and enabling successful change to reach desired goals (knowledge_for).
Here, theory may be understood as a set of assertions (Weick, 1989) or propositions. Each proposition includes one or more concepts relating to things in the physical world (including physical, biological, and social systems) and may include descriptions or explanations of how those things are related; “a declarative sentence expressing a relationship among some terms” (Van de Ven, 2007: 117). Much like what Popper would call an axiomatic system, model, or set of hypotheses (Popper, 2002: 53).
Building on systems thinking (as understanding relationships between things), each theory may be understood as a kind of “conceptual system” (Wallis, 2016a) existing in a conceptual world or ecology of knowledge (Disessa, 2002) where (for our purposes) the things in the system are concepts and the relationships between them are causal connections. As will be explained in greater depth below, a conceptual system is useful, in some way, for understanding the world of physical systems; and, for taking action with some expectation of successfully reaching goals. Examples of conceptual systems include theories, models, mental models, program theories, policy models, large scale theories, middle range theories, laws, strategic plans, and so on. Those terms will be used interchangeably in the present paper, although we will mostly refer to them as theories.
For clarity, those theories may be presented as diagrams—with boxes containing concepts (each representing something in the physical world) and arrows between the boxes providing a representation of presumed or expected causal relationships. There are many forms or types of diagrams from making simple “Venn Diagrams” to complex “GIGA-Mapping” (cf. Sevaldson, 2011). While each form may have its benefits, our focus will be on diagrams where measurable concepts (as nodes or variables) are connected with arrows (representing causal relationships) as a long history of research has shown those to have measurable structures which may be correlated with their usefulness in practical application (Wallis, 2018, 2020b).
Those diagrams may be referred to as knowledge maps; or, more simply, maps. Figure 1 shows a simple map representing the number of predators and prey in an ecosystem. With more predators, there will be a decline in the number of prey (indicated by the minus sign on the causal arrow). With an increase in the number of prey, the increased food source will lead to an increase in the number of predators.
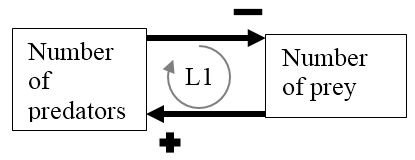
Figure 1 A simple loop
Here, it is important to recognize that the focus of this paper is on the conceptual systems (theories, models) rather than the underlying situations of the physical systems. We are focused on theories themselves as representations of “how the world works,” regardless of the source of the theory (personal experience, collaborative deliberation, formal academic analysis, etc.). As such, any theory may be situated in another meta-level of understanding where the theory emerges from, and is used in, practice (which, although important, is not the focus of the present paper).
While calls for advancing theories have been heard since the dawn of science, progress in the social/behavioral sciences has been slow. Previous calls for “more data” have not proved highly effective in advancing the social/behavioral sciences. Available data is increasing exponentially, but the quality of our theories remains staid (Wallis, 2015a, 2015b). Even “big data” (Russom, 2011; Wamba, Akter, Edwards, Chopin, & Gnanzou, 2015) while interesting and useful on some level has not served to significantly advance and so fulfill the promise of the social/behavioral sciences.
With that lack of efficacy, it has been said that organizational theory has failed (Burrell, 1997; Lewis & Kelemen, 2002) as has social theory (Appelbaum, 1970). Policies (informed by policy theories/models) seem to rarely reach their stated goals (Light, 2016; Wallis, 2011, 2016a) often leading to “worse outcomes than the previous status quo” (Beaulieu-B & Dufort, 2017: 1). Many examples of unanticipated consequences from purposeful policy actions and short-sighted practices may be found with Sterman (2012: 24).
Instead of finding improvements in theory, with attendant improvements in practice suggesting a scientific revolution (Kuhn, 1970), recent decades have seen something more akin to a celebration of postmodernism; an explosion of insights. For better or worse, those many insights and associated theories have been viewed as part of the problem of disciplinary fragmentation. That process may be seen where scholars use a variety of terms; perhaps to increase the novelty and attractiveness of their work (Hovorka, Birt, Larsen, & Finnie, 2012). Such fragmentation (and confusion) seems common across the social/behavioral sciences (cf. Bakker, 2011; Ledoux, 2012; Lewis & Kelemen, 2002; Newell, 2007) and perhaps beyond. Fragmentation may be seen where each scholar has great expertise in a small area so that each expert seem like a novice to other scholars (Lipton & Thompson, 1988).
It seems, therefore, that we are in need of a new way to develop our theories, and so our sciences. To that end, this paper will conduct and present a preliminary exploration of the causal loop structure of conceptual systems (conceptual loops) to answer this research question: How might we more rigorously evaluate loops presented in theories to support our ability to develop theories that are more useful in practical application?
A Structural Path Forward
Because theories are ubiquitous across disciplines, and those theories have a kind of measurable internal structure, it is anticipated that the same general ideas about structure may be applied to theories of all sciences. By measuring changes in the structure of theories as they evolve over time from lesser to greater usefulness, we may be able to identify what kinds of changes support improvements. With such insights, we may be able to accelerate the development of our theories and our sciences to more rapidly and effectively understand and resolve the wicked problems of the world.
Past studies of theories have used Integrative Propositional Analysis (IPA) to evaluate their structures based on the number of concepts (“breadth” or “simple complexity”) and a measure of causal connectivity (“depth” or “systemicity”). And, so far, the more structured theories seem to be more useful than theories that are less structured understanding situations and reaching goals (Wallis, 2016a). We will delve into IPA in greater detail below.
While loops have been identified as a useful sub-structure within theories (Wallis, 2016b), IPA has not had a specific method for evaluating loops. The present paper is a step forward to remedying that lack because, aside from a general understanding that “more loops are better,” no clear guide seems to exist as to how many loops are required in a theory to make it better (more useful for understanding situations and enabling effective change).
In the present paper, that IPA stream of research is continued with a focus on the structure of loops within theories with the idea that by building theories with more loops it is expected that theories will become more useful in practical application for understanding situations and taking effective action to reach goals.
To clarify, this process (and this paper) is not about finding examples from the natural sciences that may be applied through metaphor to gain insights elsewhere (although those may be interesting). Nor is this paper about seeking some “consensus among stakeholders” where scholars (somehow) agree to use a common theory regardless of its efficacy. Instead, in the present paper, we will look at the internal structure of theories for clues as to what makes them more efficacious or useful for understanding and resolving problems in the social/physical world.
It is worth noting that, for the present paper, theories are the subject of analysis. That is, by counting the structural components (e.g., concepts, causal connections, loops, etc.), we gain in data that will help us to better understand how our theories are structured.
Systems, Dynamics, Loops, and Maps
In this section, we briefly cover some background perspectives to orient readers of various disciplines to the science of conceptual systems (SOCS).
Systems thinking suggests a way of understanding the world by understanding interactions (Sterman, 2012). “Systems thinking is about understanding these interactions and interconnections and identifying the leverage points to solve the problems in the organization.” (Vemuri & Bellinger, 2017: 2). Generally, systems thinking encompasses a variety of more specific perspectives including cybernetics and systems dynamics (Schwaninger, 2015).
One key idea of systems thinking is that we expect to identify similar patterns, or isomorphic similarities, (Friendshuh & Troncale, 2012) across differing fields of study. And, by finding such similarities, improve our understanding within fields, along with our interdisciplinary understanding (among many fields). Such understanding improves our ability to take effective action and reach our goals. Those isomorphies are visible across a vast range of theories (conceptual systems) most clearly as concepts and causal connections between them that exist in so many theories. Another pattern, although less frequently found in theories of the social/behavioral sciences, is the causal loop. Loops (of course) are perhaps most studied in the field of cybernetics and systems dynamics.
Emerging in the 1940s, the field of cybernetics (overlapping with systems sciences) has been gaining interest, particularly in Asia and Europe (Umpleby, Wu, & Hughes, 2017). Applied across many (if not all) disciplines, cybernetics is “concerned with circular causal mechanisms in biological and social systems” (Umpleby, Wu, & Hughes, 2017: 34). Those kinds of loops may be easily seen in a simple form where your home thermostat switches the furnace on when the house is too cold and off when the house is warm enough. Here, we extend that definition to include “conceptual systems.”
The study of cybernetics is based primarily on ideas of feedback, control, and guidance (Schwaninger, 2015). “Feedback is used in virtually all scientific fields, from physics, chemistry and ecology to the social and economic sciences, as a principle for the explanation of system behavior and the design of systems” (Schwaninger, 2015: 56). Because loops are seemingly ubiquitous (as are theories) across the sciences, we may be able to use insights gained from identifying causal conceptual loops in theories (which may be different from feedback loops) of one science to better understand and develop theories in another science. Particularly, if we are able to identify the role played by loops within the causal structure of theories.
Within the broader study of systems, Systems Dynamics (SD) has evolved to be, “A methodology and discipline for the modeling, simulation and control of dynamic systems. The main emphasis falls on the role of structure and its relationship with the dynamic behavior of systems, which are modeled as networks of informationally closed feedback loops between stock and flow variables [boxes/concepts]” (Schwaninger, 2011: 8974). It is worth noting that, “Linking feedback loops and system behavior is part of the foundation of system dynamics, yet the lack of formal tools has so far prevented a systematic application of the concept, except for very simple systems” (Kampmann, 2012: 370).
In SD, experts use complex processes and formulae to simplify complex theories and find leverage points where policy actions might have the greatest effects (Oliva, 2015; Saleh, Oliva, Kampmann, & Davidsen, 2010). Even for rigorous processes, some element of judgement is required, along with some computational expertise (Oliva, 2015: 208). Another SD approach is to identify the “dominant” loops within a theory (Duggan & Oliva, 2013; Hayward & Roach, 2017). Which, while interesting, requires higher mathematical skills than are easily accessible to many researchers.
Those methods, to the best of this author’s knowledge, are not used to compare theories to show which ones might be the more accurate or useful interpretation of the physical world. And, for many scholars and practitioners, that level of expertise may not be readily accessible. One goal of the present paper, in contrast, is to understand how we might evaluate the whole model in a way that balances rigor with accessibility.
“The SD method relies mostly on the enumeration of feedback loops.” (Wakeland & Medina, 2010: 17) but, “How many feedback loops does a given system have? Unfortunately, there are no general formulas for finding the loops for a given system, short of direct enumeration.” (Kampmann, 2012: 374); a problem that exists in parallel for identifying loops in the physical world, as well as identifying loops on a map. Both may be highly complex and subject to misunderstanding.
For clarity, it is important to repeat that this article will be investigating loops found in theories (conceptual loops) rather than the many different kinds of loops that may be found in physical or social systems. While we may interpret different kinds of systems as having different kinds of feedback (e.g., verbal or electronic), we look at conceptual systems differently—focusing on conceptual loops.
To put it another way, we are investigating the conceptual systems which represent those other systems. Such representation may be mechanical and simplistic, regardless of the complexity of the physical/social system represented. For example, a social system that is highly complex and non-linear may be represented by a theory that is simple and linear. Of course, such a linear representation is thought to be less useful than a conceptual system that contains multiple loops. Theories with more loops are generally expected to provide a more accurate, and therefore more useful, representation of complex, nonlinear social systems.
Importantly, in this study, we are learning how to analyze the structure of our conceptual systems to see how useful a representation they provide for understanding and enabling change in those physical/social systems. So, before taking action (for example to change a social system), we will have an indicator for whether that action will be successful, based on the structural qualities of the theory used to inform or support that change.
To help understand the structure of our theories, we use diagramming and other related forms of visualization. These are central to design thinking and design practice supporting creativity and synthesis (Sevaldson, 2011).
In the present paper, we are seeking to find more accessible techniques that may be easily acquired and applied by scholars and practitioners across a variety of scientific disciplines to improve their theories and accelerate the development of their fields. Optimally, such a process will allow the field to identify better theories that may be the focus of more advanced forms of research.
Three streams of research supporting a structural perspective and the usefulness of maps
As noted above, a conceptual system is a set of interrelated propositions—a theory—reflecting actionable knowledge and/or an understanding of how the world works. Briefly, to provide an orienting background, the science of conceptual systems may be found in at least three streams of research. From the field of political psychology, the measure of “Integrative Complexity” (IC) is applied to texts (typically found in personal communications or public speeches). IC may be defined briefly as a measure of conceptual complexity including the differentiation and integration of concepts held by individuals and/or groups that enable more effective information processing and decision making (Suedfeld & Tetlock, 1977). Research in that stream shows that individuals and teams whose texts reflect a higher level of structure are generally more successful at reaching their goals (Suedfeld & Rank, 1976; Suedfeld, Tetlock, & Streufert, 1992; Wong, Ormiston, & Tetlock, 2011). Suedfeld (2010) provides a 30-year history of that stream.
From the field of education, the “systematicity” stream is generally focused in the classroom, where students with a better understanding of the course material are said to have knowledge with greater structure. Drawing on Fodor and Pylyshyn, Phillips and Wilson (2014) suggest that, “Systematicity is a property of cognition whereby the capacity for some cognitive abilities implies the capacity for certain others.” That capacity is demonstrated when students create concept maps showing terms they’ve learned, along with arrows linking those terms, and lines showing how the terms might be related in some kind of hierarchy. An expert then scores the concept map to determine the students’ level of mastery (reflecting capacity for cognition on the topic of study). Novices tend to create simplistic maps with low levels of structure, while experts create complex maps with high levels of structure (Novak, 2002, 2010). Such advancement is also seen from the perspective of psychology where, “According to Piaget’s developmental theory of learning, individuals’ assimilate external events and accommodate them to develop a mental structure the facilitates reasoning and understanding” (Gray, Zanre, & Gray, 2014: 30).
While the IC and systematicity perspectives support the general notion that having more structured knowledge is more useful in practical application for understanding situations and making decisions to reach specified goals, neither was developed to evaluate formal theories. So, we will not be using those methods to study theories in the present paper (future research may explore the overlap between them).
Instead, we will focus on a third stream of research, emerging from the systems sciences. “Integrative Propositional Analysis” (IPA) is used primarily for analyzing formal theories such as those as presented in peer reviewed literature, IPA is a methodology used to evaluate and determine the structure of theories based on the number of concepts and the number/direction of causal connections between them (Wallis, 2016a). IPA is a relatively new methodology, which suggests a limit to its potential usefulness. Also, while IPA has been used to show a general correlation between the structure and usefulness of theory that relationship has not been quantified with great accuracy.
In general, IPA has shown that with more structure, theories are more useful for decision making in practical social/physical world situations. Because theories, with greater and lesser levels of structure, are ubiquitous across all sciences, IPA has been applied to successfully evaluate theories from many disciplines including physics (Wallis, 2010), psychology (Wallis, 2015b), sociology (Wallis, 2015a), policy (Wallis, 2011), strategic planning for academic institutions (Wallis, 2020b), applied social research (Wright & Wallis, 2019), and others. IPA has also proven useful for integrating theories within and between disciplines for improving the structure, and so the potential usefulness, of those theories (Wallis, 2014b, 2018, 2020c) enabling greater sustainability and morality while avoiding the limits of our own human cognition (Wallis & Valentinov, 2016a, 2016b, 2017).
Despite the clear importance of causal loops for an understanding of how the world works (evidenced by their importance in multiple fields of study), research on mental models shows that few incorporate any loops. Axelrod (1976) found virtually no loops processes in the cognitive maps of political leaders. Dörner (1980, 1996) found that people tend to think in single-strand causal series and had difficulty in systems with side effects and multiple causal pathways, much less loops. Sweeney and Sterman (2007) found limited recognition of feedback processes among both middle school students and their teachers.
That lack of loops may be related to cultural limitations. Where “Western” thought tends to be more linear than Asian thought (Wallis, 2016b). African logic (reflected in the concept of Ubuntu) also tends to be more circular, representing a higher level of interconnectedness or interrelatedness for understanding organizations and contexts (Chilisa, Major, Gaotlhobogwe, & Mokgolodi, 2015; Wallis, 2019). Whatever the underlying reason(s), we can improve our ability to understand real-world systems through our conceptual systems by creating diagrams such as maps, mind maps, concept maps, and so on.
Benefits of Mapping
Mapping supports clarity of understanding (Hovorka et al., 2012) and collaboration (Bryson, Ackermann, & Eden, 2016) at least in part because maps help alleviate the limits of human cognition (Bureš, 2017). Mapping is also beneficial because it helps us to integrate or synthesize diverse perspectives more easily and effectively. This is important because, “Collaboration and cross-sector collaboration have therefore emerged as hallmarks of the new approach in which public managers frequently must work jointly with nonprofit organizations, business, the media, and citizens to accomplish public purposes” (Bryson et al., 2016: 912) which is important because “collaboration is usually difficult and success is hardly assured” (p. 912). The turn towards visual mapping also supports clarity, accountability, trust, and coordination through interdependent goals because assumptions can be “on the table” visible to all (Wallis & Wright, 2015).
As abstract representations of physical world systems, it is general understood that, “The truth and quality of the models [theories] used hinges primarily on the correct match of the model [theory] with the concrete (‘real’) [physical] system in focus” (Schwaninger, 2015: 572). A key assumption of the present paper is that our best (most useful) representations of the physical world, our laws of physics, include causal loops as may be seen in Figure 4—a causal loop representation of Newton’s second law. We may reasonably expect that developing loops in theories of other sciences will similarly lead to improvements in the usefulness of those theories thus improving practices and practical success in many fields.
Before moving on to compare maps of theories, some clarity in terminology may be useful because many of our fragmented fields use different terms when referring to the same (or very similar) things. For this paper, we will use the term “map” to refer to a theory presented as a diagram (which might also be referred to as a loop diagram, graph, or directed graph). Links and edges will be referred to as causal arrows or more simply “arrows.” And, we will use the term “concept” (or “box” on a map) instead of terms such as nodes, points, variables, or vertices.
It is also worth noting that our focus will be exclusively on causal theories. That is, where the map shows how changes in one or more things cause changes in one or more other things. That causal perspective is foundational to scientific understanding (Pearl, 2000). Indeed, “[S]tudies of learning, attribution, explanation, reasoning, judgement and decision making all suggest that people are highly sensitive to causal structure” (Sloman & Hagmayer, 2006: 408).
Generally, as noted above, the perspective from the systems sciences seems to suggest that having more loops in a theory will provide a better map; a more useful representation of the physical world. While this seems intuitively correct, it does not seem to be supported by empirical studies; relying, instead, on illustrative examples of how systems work in the physical world (e.g., thermostats and furnaces). And, how they fail when a loop becomes disconnected (such as a thermostat failing to switch on its furnace because of a lack of communication between the two). The present paper will focus on addressing that lack of empirical evidence to find out the extent to which our assumptions may be warranted.
Methods for Measuring Loops and Structure
While it seems important to look for and identify loops (Deegan, 2011: 21) the focus seems to have been on simply identifying or finding what loops exist (or seem to exist), in the physical world, rather than relating the quality and quantity of loops with the usefulness of the theory. In this section, we review a variety of perspectives to see how we might better understand and evaluate loop structures. These measures will inform the present methodology, which will be used to evaluate the structure of theories to help understand what strategies we might use to accelerate the improvement of our theories.
In the field of business studies, Senge, Kleiner, Roberts, Ross, and Smith (1994) show how loops may be used to understand challenging situations. They provide various arrangements of loops relating to organizational issues (e.g., “limits to growth,” “fixes that backfire,” and “tragedy of the commons”). And, those patterns suggest where intervention might have some successful results. Those patterns typically include only two to three loops (ibid.: 150); while, in contrast, the overall process encourages creating maps with more loops to provide a more useful understanding of complex situations. What is missing from that publication is some reasonably objective measure of “how many” or “what kind” of loops might be optimal. Instead, the authors recommend that a group stop adding loops “after a few interdependencies become apparent” (Senge et al., 1994: 163) and instead of continuing to improve their understanding, instigate a conversation about the emerging themes of the map and implications for action.
What ‘becomes apparent’ for one, does not necessarily mean apparent for all. What might happen when one faction desires to take action while another faction desires continued exploration? What if one person or faction holds a hidden agenda that is not reflected on the map? Such situations provide the opportunity for conflict; so, having more objective methods for evaluating the usefulness of maps may provide some beneficial guidance to practitioners and researchers.
In systems dynamics (SD) “Network analysis provides a suite of quantitative techniques that can summarize the structure of a network and quantify the importance of its elements. Understanding the structural features of a network as a whole can provide key insights into the ease or difficulty by which information, influence, or physical matter flow through the network” (McGlashan, Johnstone, Creighton, de la Haye, & Allender, 2016: 2). Using an SD perspective, we might ask how influential each concept might be on the map as a whole; how central it is or how closely connected each concept might be compared with the other concepts on the map (McGlashan et al., 2016). Those might be thought of as “leverage points” from a structural perspective (Wallis, 2020b; Wright & Wallis, 2019), where a small amount of effort may lead to a large amount of change. Again, while estimating the importance of certain concepts, the SD approach does not seem to provide strong guidance for enumerating loops.
In cybernetics, Umpleby (2018) suggests building maps with a combination of positive and negative loops (basically, loops whose effects balance one another, one causing increase and another a decrease in some concept/box). If most or all the loops are mutually supporting, it would suggest that there will be “runaway” effects. For example, consider a charity whose map shows then that conducting fundraisers will generate more money and that the money raised can be used to conduct more fundraisers. If the theory were valid, they could set such a plan in motion and soon control all the money in the world. As that is a highly unlikely scenario, there must be something missing from the map; one or more balancing loops that limit the charity’s ability to raise funds (e.g., “donor fatigue” resulting from a large number of fundraising events). While identifying balancing effects seems potentially interesting, there is no quantitative evaluation of the number of loops or how they may be balanced.
Seeking to include all the concepts of the theory within those loops, another approach is to identify and enumerate independent loops sets (ILS), with a focus on the “shortest loops possible” (Oliva, 2004: 322). Such an approach seems reasonable; first, because by comparing the number of concepts included in all loops, we can identify what percentage of the total number of concepts in the theory are accounted for. That is to say, it seems reasonable to assume that the better theories will have a higher percentage of their concepts as part of one or more loops. That assumption, as yet, seems to be unfounded. Second, by focusing on the shortest loops, we may reduce the confusion found in looking at large and complex theories that may have longer loops (including more concepts) and/or multiple overlapping loops. That is not to say that the longer loops are meaningless or irrelevant, only that this approach may be used as a starting point to making complex maps more comprehensible. And, of greater importance for evaluating maps, focusing on the smallest loops may provide a more objective way to view theories so that differing scholars may reach the same or more similar conclusions about the similarities and differences in structure between theories.
Bureš (2017) suggests it may be useful to consider the, “multi-input and multi-output (MIMO) variables [concepts/boxes]” (p. 5). That is, concepts with more than one arrow pointing inward and more than one pointing out or away from each concept/box. Similarly, Integrative Propositional Analysis (IPA) suggests that theories should be created with at least two inputs for each concept on the map (cf. Wallis & Wright, 2019). A concept with two arrows pointing directly at it is said to be concatenated. And, like a dependent variable influenced by two or more independent variables, is held to be better understood. So, a map with more concatenated concepts will provide greater understanding and so be more useful. While these methods evaluate the structure of the map, neither approach is directly used for the evaluation of loops.
Delving more deeply into IPA, from Wallis (2015b: 371), Integrative Propositional Analysis is a six-step process: 1. Identify the propositions within a theory. 2. Diagram the causal relationships between the concepts within the propositions. 3. Combine those smaller diagrams where they overlap to create a larger, integrated, diagram. 4. Count the total number of concepts to determine the (simple) Complexity of the theory. 5. Identify and count the concatenated concepts (those that have more than one causal influence). 6. Calculate the Systemicity of the theory by dividing the number of concatenated concepts by the total number of concepts.
From that structural perspective, the measure of Systemicity may be used as an indicator of the map’s potential usefulness for choosing actions and so reaching goals. IPA is also limited in that it does not consider underlying data. Thus, a theory may have a high level of structure even though it has no counterpart in the physical world. Other measures must be used to ascertain the validity of the data supporting the theory.
Please note that the measure of “systemicity” from IPA is different from the above-mentioned approach of “systematicity.” The difference is not important to the present paper as we will use only systemicity here.
Although not all of the above measures expressed or implied specifically suggest or require enumerating loops, they do apply to structure and so we will apply a variety of them to the present study of evaluating theories. This will provide methodological plurality enabling a more effective comparison of the theories under analysis and the methods used. Including:
- The number of smaller loops (two concepts);
- The number of larger loops (three or more concepts);
- Percent of all concepts included in loops;
- The number of fully positive loops;
- The number of fully negative loops;
- The number of loops combining both positive and negative connections;
- The ratio of positive/negative signs on causal connections;
- Number of DIDO or MIMO concepts;
- IPA measure of concatenated concepts;
- Number of leverage points, and;
- IPA measures of complexity and Systemicity.
In the following analysis, we use these measures to analyze the structure of theoretical models from multiple perspectives as their structures evolved over time from lesser to greater usefulness. This is expected to help us see how their structures changed; and so, what inferences we might make for evaluating and improving our theories of the present to develop more useful theories in the future.
Subject of Analysis: Evolving Theories
In this section, we present in map (diagrammatic) form a number of theories for analysis using the methods and measures described in the previous section. First, we will present a series of theories from physics, followed by a series of theories from the health sciences. In each series, the theories may be understood as evolving from lesser to greater usefulness in practical application. The examples will be followed by the results of the analysis, discussion, and recommendations for research and practice.
For each figure, concepts are represented as boxes with causal relationships as arrows (with positive or negative influences indicated), between them. Loops are noted as lighter shaded, circular, arrows and enumerated L1, L2, etc.
Physics: From Aristotle to Newton
Focusing on the nature of “force” in physics, Stinner (1994) also examined the evolution of a theory through history. Drawing on Stinner’s text, Aristotle’s version of force is presented in Figure 2.
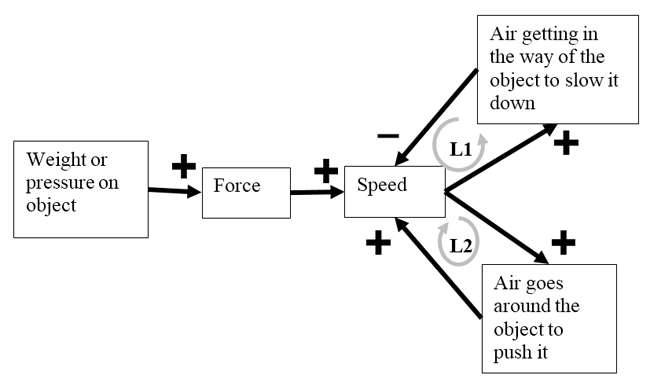
Figure 2 Aristotelian conceptualization of force
While Figure 2 has two loops, it is worth noting that the loop involving air going around the object to push it was not supported by data; that was merely a conjecture to account for why the object did not stop immediately when pressure or force was removed.
Moving on through the evolution of the theory, according to Stinner (1994), in the middle ages, John Burdian had come up with another version (Figure 3). For Burdian, when the impressed force is removed, some force (somehow) would continue to push the object, but would eventually die out. Again, this part of the theory was based on conjecture.
While Burdian’s version may seem to make more sense than Aristotle’s, it still did not provide sufficient explanation of the concepts to launch rockets into orbit (or, more appropriately for the time, predict the trajectory of catapult projectiles).
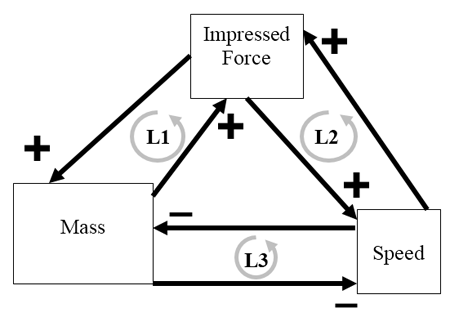
Figure 3 Force according to Buridan (Impressed force = mass x speed)
Figure 4 shows a causal diagram of Newton’s famous Second Law (F=ma) with what might be called a “triadic” structure of loops. That law is entirely supported by data. And, it has proved highly useful for (among other things) launching satellites which facilitated global communication, weather observation, and more. In short, more useful than the theories presented in Figures 2 and 3.

Figure 4 Newton’s Second law (F=ma)
In comparing Figures 3 and 4, it is worth noting that they are structurally identical (same number of boxes, same kinds of connections). Figure 4 (Newton) includes “acceleration” instead of Burdian’s “speed” (Figure 3). Also, Figure 3 includes “Impressed force,” instead of Newton’s “Force.” That notion of impressed force (and related assumptions) were not supported by data. So, scholars seeking to improve their theories should keep in mind that they must be supported by data—structure alone will not suffice.
Returning to our focus on structure, it is worth noting that an alternative explanation of loops might be perceived for Figures 3 and 4. That is, using Figure 4 as an example, one loop may be seen passing through all three concepts while a second loop may be seen passing through all three concepts in the opposite direction. Those loops are ignored in favor of the smaller loops because the two large loops appear to be in parallel with each other and could conceivably be seen as redundant. In contrast, the three loops containing only two concepts each are clearly not redundant. We would not consider Figure 4 to have five loops because that would involve counting each arrow twice—which would introduce manifold uncertainties in evaluating structure.
The sequence of above maps (Figures 2, 3, and 4) generally suggests a progression from lesser to greater understanding and usefulness. The results of the previously described analyses are summarized in Table 1 according to the various measures of structure from the previous section.
Public Health: Progression of a Conversation
As may be seen in the previous sub-section, historical examples of theories may be found in the natural sciences (especially physics), from which we may see the evolution of theories from ancient times to the present. And, with that advancement, we may identify structural components and so identify and infer relationships between the structure of the theories and the usefulness of those theories. Such a history, however, does not yet seem to be available for the social/behavioral sciences. So, for the purpose of the present analysis, we will look at a set of theories drawn from an online conversation where (through conversational turns) the map was improved. Although incomplete, the four theories in Figure 5 may be seen as representing an evolution in knowledge or understanding; with presumed evolutionary improvement in usefulness of that theory for decision making for taking action and reaching goals.
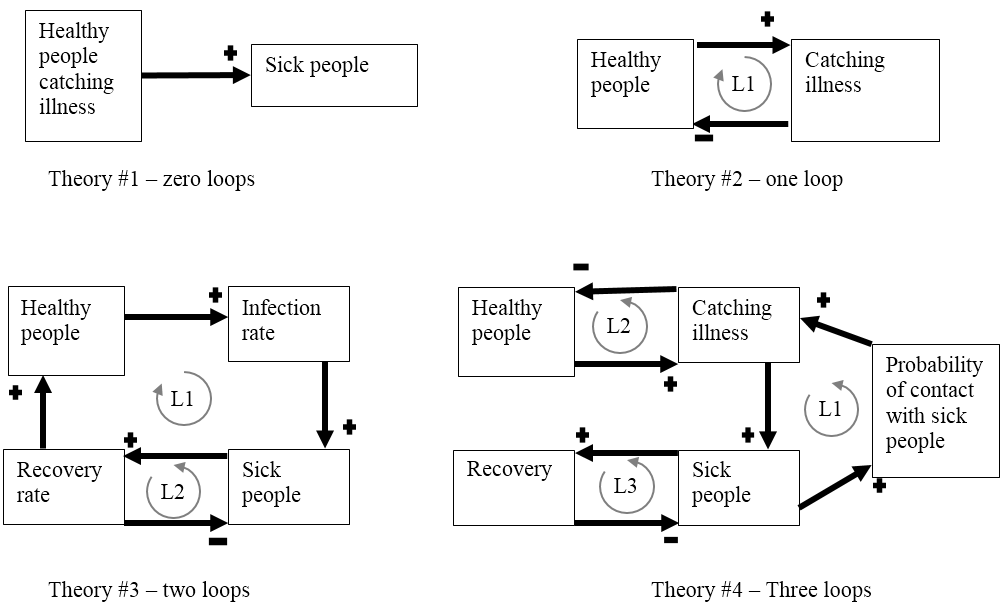
Figure 5 Progressively valid theories of public health: Derived from: link
Each theory in the series from Theory #1 to Theory #4 may be understood as an improvement of the previous theory. That is, each map represents a deeper knowledge or understanding of the situation as each version built upon the previous through a conversation among experts. The results of the analytical methods (from the previous section) applied to the theories in Figure 5 are summarized in Table 2.
Results of Analysis
In this section, we summarize the results of analysis from the methods previously developed and applied to the theories of the previous section. Those results are shown in Tables 1 and 2, and explained below.
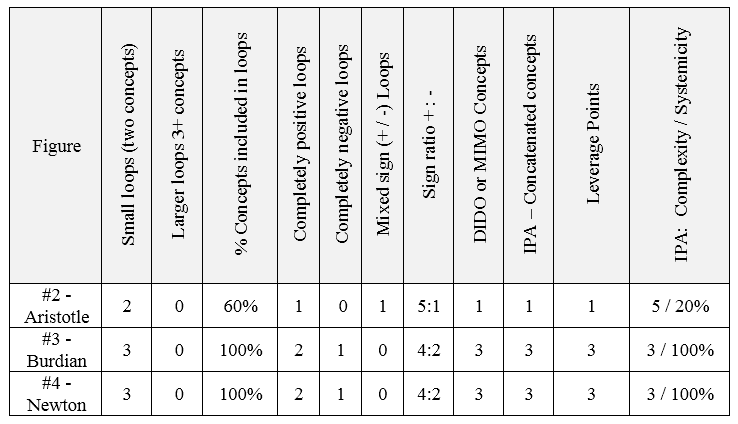
Table 1 Summary of results: Evolving theories of physics
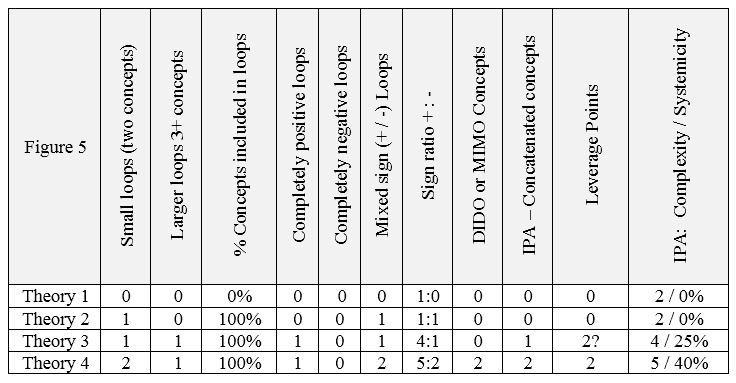
Table 2 Summary of results: Evolving theories of public health
Looking at Tables 1 and 2, we begin with the far left hand column which indicates the theory under analysis in order from top to bottom of increasing usefulness for in explanation and application.
The first column of data (after the column listing the theories) shows the number of loops where those loops contain only two concepts (and two causal connections between them). Key to the present study, we do indeed see that the number of loops increases as the theories improve. This serves as an important validation for a key assumption of cybernetics and systems thinking.
The second column looks at larger loops; those with three or more concepts. Interestingly, while there are none of these for theories of physics, we see one for two of the theories from public health. This may indicate an interesting question for future research. Should the better theories of the natural sciences have no larger loops while the theories of the social/behavioral sciences have more?
In the third column, of data we see the percentage of concepts included within loops. Again, there is a general increase in this percentage as the theories improve suggesting that this may be a useful measure for evaluating the potential usefulness of theories.
The fourth column identifies the number of completely positive loops in each theory. That is, those loops where both or all of the arrows reflect positive causality (e.g., more of A causes more of B). Here again, we see a general increase suggesting that this may be a useful measure of improvement in theories.
Next, we see the number of completely negative loops in the fifth column. That is, those loops where both arrows show a negative causal relationship (e.g., more of A causes less of B). Interestingly, while we see an increase in the physical theories of Table 1, the theories of public health in Table 2 show none at all. This will be discussed below in the section titled, “Pluses and minuses.”
In the sixth column of data, we have the number of loops for each theory where the causal arrows include both positive and negative causation. Interestingly, the theories of physics in Table 1 show a decrease while the theories of public health in Table 2 show an increase in these kinds of loops. This will be discussed below in the section titled, “Plusses and minuses.”
The seventh column considers the ratio of signs on the causal arrows for each theory. That is, the number of arrows representing positive and negative causation. Here, we see an interesting progression; as the theories evolve toward greater usefulness, the ratios also seem to evolve. This may be another area for future study.
The eighth column indicates the number of concepts for each theory that is DIDO (dual-in, dual-out) or MIMO (multiple-in, multiple-out) referring to the number and direction of causal arrows to and from the concepts. This approach (as noted above) has been hypothesized as a potential measure for the usefulness of theories; and the present study provides some preliminary support for that hypothesis.
In the ninth column, the number of IPA concatenated concepts are shown. Briefly and simply, those are the concepts with two causal arrows pointing at them. Much as a concept is better understood when it has two independent variables pointing at it, these concatenated concepts may serve as a proxy—a very simple measure—for the explanatory power of each theory. As expected, there is a general increase in the number of concatenated concepts as theories improve.
In the tenth column, we look at the leverage points for each theory. A leverage point is a concept that is included in (at the intersection of) two or more loops. While we see an increase in leverage points in line with the improvement of the theories, Theory 3 in Table 2 presents an issue. The two loops of that theory overlap so that both loops include two concepts (“Recovery rate” and “Sick people”). This confusion and potential resolution will be addressed in the section below titled, “Reducing redundancies.”
In the last (11th) column, measures of IPA are shown. These are included because IPA has served as an effective measure of systemic structure, and so predictor of usefulness, in theories. This serves as a check between existing methods and the methods being developed in the present paper. There, complexity (simple complexity) shows the number of concepts in each theory. Systemicity, is the measure of systemic structure. As expected, there is a general trend toward increasing values in both these measures. The exception being in Table 1 where the Aristotle’s theory contains more concepts than later versions. This may be seen as an indicator of increasing parsimony which occurs as theories evolve. Table 2 shows no increase in parsimony suggesting that this theory is as yet not fully mature.
To summarize this section, and note an important contribution of this paper, these structural measures all seem to be effective for evaluating the potential usefulness of conceptual systems (theory, models, etc.) because they seem to correlate (at least roughly) with the increased usefulness of the theories. And, as such, any of these measures may be used to point the way to constructing theories that are more effective for understanding and resolving the wicked problems of the world. Because this is a preliminary study, there are many opportunities for future research.
Summary and Recommendations
Here, we have been seeking to develop techniques that may be accessible to a wide variety of scholars and practitioners across the scientific disciplines to rigorously and objectively evaluate and improve their theoretical models from a structural perspective and accelerate the development of their fields. While this is a preliminary study, a few additional insights may be found.
Importantly, this study provides empirical support to the general assumption that our theories will be more useful when they include more loops; and, to the idea suggested by Oliva (2004) that we have better theories when more of the theory’s concepts are included in loops. Also, this study supports the more specific suggestion by Umpleby (2018) that a more realistic and useful theory will include positive and negative loops that “balance” one another.
Also, generally, these results support the validity of multiple methods and techniques that might be used to evaluate the structure of theories; and, therefore, may be used as a guide to improve the usefulness of our theories. More specifically, this study supports IPA measures of complexity and systemicity as indicators for the structural quality of theory (Wallis, 2016a; Wallis & Valentinov, 2016b; Wright & Wallis, 2019). This study also supports DIDO (dual input, dual output) and MIMO (multiple input, multiple output) as indicators for theory quality (Bureš, 2017). IPA and DIDO/MIMO can and should be applied to accelerate the advance of scientific fields by comparing and synthesizing theories to develop theories that are more useful in practical application.
Third, in comparing theories of physics and public health, it is worth noting that in both fields theories are more useful when they have more leverage points. Indeed, in the best of the present examples (Newton’s Second Law), all the concepts are also leverage points. That seems to suggest that we can build better theories by creating them with more leverage points. Recalling, of course, that these are “structural” leverage points (concepts held in common by two or more loops) rather than the more “intuitive” leverage points of Meadows (1999). For a discussion on this distinction please see Wallis (2020b).
Fourth, the idea of abstraction seems to be relevant here. Not, however, in the sense that a theory is an abstraction of the physical world; rather, that a theory may be more effective or useful when its component concepts are all at a similar level on some scale of abstraction (Wallis, 2014a). While Newton’s concepts of force, mass, and acceleration seem to be similar on some scale of abstraction, Figure 6/Model 4, contains concepts that are clearly at different levels of abstraction. We have some concepts that are more concrete (number of sick people) and others that are more abstract (probability of contact with sick people). It may be worth exploring how each of those might be “shifted” to a more common level on some scale of abstraction. Alternatively, it may be useful to separate them into two different theories—each working at its own level of abstraction. More research is needed in this area to clarify the potential benefits of this approach to abstraction.
Naming the Method: IPA “x”
To summarize, the present research suggests a range of measures that may be used for evaluating the structural quality of theories thus supporting accelerated advancement in many fields of science. For those using Integrative Propositional Analysis (IPA) to evaluate and improve the structure of and usefulness of theories and strategic plans according to their Breadth/Complexity and Depth/Systemicity, the following new measures are suggested on a provisional or “experimental” basis (IPAx).
- Loops should be counted according to the shortest possible path. Parallel (redundant) loops should not be counted.
- Theories with more loops are expected to be more useful in practical application than theories with fewer loops.
- Theories with more leverage points are expected to be more useful than theories with fewer.
- Theories with a higher percentage of concepts included in loops are expected to be more useful than theories with a lower percentage.
- Loop/sign balance—Theories are expected to be more useful when the ratio of positive to negative loops (or signs) is closer to 2:1.
While preliminary in nature, these results suggest that scholars and practitioners can and should use the above measures to evaluate the structure of theories for choosing which one(s) to use in practice and as a guide to improving the usefulness of theories through research (by conducting research focused on improving one or more of the measures).
These insights should prove useful for the System Dynamics community as an approach for quantitatively differentiating between models according to their structure. Further research may be interesting in this area focusing on (for example) the use of stock-and-flow diagrams to represent theories.
Insights, Conversations, and Future Research
In this section, we will go into greater depth on a few insights that may be gained from a careful parsing of the data. Those, in turn, will lead to suggestions for additional research.
Pluses and minuses
Umpleby (2018) suggests that loops should balance. That is, positive and negative loops should intersect to avoid unrealistic understanding of a situation. And, in both the health sciences and in physics, we see that kind of structure. However, it is interesting to note that we see two different kinds of balancing structures. In Newton’s law, there are three dyad loops. Two that have both their arrows representing positive causation while the third has both its arrows representing negative causation. In contrast, the theories of public health have self-balancing loops with one positive and one negative arrow each.
The end result for both seems to be a balancing effect on the concepts of the theory. So, Umpleby’s suggestion seems to stand. However, the difference does raise questions. Is there an optimal structure for theories in which the balance is “within” dyads (as in public health theories), or is the optimal balance “between” dyads (as in Newton’s Law)? Or, is one more appropriate for physics while the other more appropriate for the social/behavioral sciences (and, if so, why)? Additional research may lead to new insights into the construction and development of more effective and useful theories.
An alternative approach also presents itself if we step back from a loops perspective to more simply evaluate the signs on the arrows (representing positive and negative causation). Enumerating the number and type of signs for each theory map of our analysis provides a sign ratio (note in Tables 1 and 2). Recognizing, again, that this is a preliminary study, it seems that theories with sign ratios closer to 2:1 are more likely to be useful in practical application.
Rather than simply providing “a combination” as Umpleby suggests, the present results advance the science by suggesting that for a theory to provide the most realistic and useful representation of the world, it should include a ratio of two positive loops to one negative loop according to Newton’s law (Figure 4) and a similar ratio for more advanced theories in the social sciences such as Theory 4 in Figure 5. More study is needed to better understand how we might evaluate loop ratios.
This structural perspective of balancing loops allows researchers who are developing theories or strategic plans, the ability to “see the invisible” and identify directions for additional research and practice that will accelerate the development of the theory toward greater usefulness—more effective application in practice. For an abstract example, if a theory is presented where all of the theory’s loops are all pointing in one direction (e.g., all are positive), the researcher should start looking for additional concepts and causal connections pointing in the other direction.
Reducing redundancies
Another issue arises with counting the number of loops where it may be suggested that the shortest loop is best (Oliva, 2004, 2015; Saleh et al., 2010). And, indeed, that is what we see in Newton’s Law (along with other laws of physics that are highly useful in practical application).
In contrast, in evaluating the number of loops and leverage points for Theory 3 (Table 2, Figure 4), some confusion arose. The redundant loops made it unclear just how the theory should be evaluated.

Figure 6 Redundant loops and redundant leverage points
As an abstract example, Figure 6 shows the L-1 (A-C) loop as the shortest path (fewest connecting arrows). In contrast, loops formed by B-D and by E-F-G are longer (more connecting arrows included in each loop) and in parallel with the A-C loop. For evaluating the number of loops, this suggests that Figure 6 should be seen as having only one loop.
Another “clue” here is that both A and C seem to be leverage points for all three parallel paths. While more research is needed, it seems intuitively strange, or at least confusing, that there are two leverage points connecting three loops. It is unclear which “one” leverage point is best; which one might be “the” leverage point. To improve the quality and clarity (and so, according to a structural measure, the usefulness) of our maps, it seems that only one leverage point should exist at the intersection of two loops. Although, with more complex theories, it may be reasonable that one leverage point may exist at the intersection of three or more loops. More research is needed to support or refute that assumption.
In comparison to the confusion of loops in Figure 6, Figure 7 shows three distinct loops (L1, L2, L3) because there are no arrows that might be considered parallel, redundant or overlapping—only overlapping concepts. Those overlapping concepts, existing at the intersection of two or more loops, seem to be valid leverage points. A is a leverage point at the intersection of L1 and L2, C is a leverage point at the intersection of L1 and L3.

Figure 7 Three loops with two leverage points
That process may be understood as a way to reduce the complexity of a theory without unduly sacrificing its explanatory capacity. Following Stinchcombe (1987), Wright and Wallis (2019, Appendix A), suggest reducing linear redundancy by removing intermediary concepts from a causal chain. For example, the linear causal chain: A → B → C → D, could be represented as A → D.
With this structural perspective, loops are more easily differentiable, yet still integrated. And, while more research is needed, those measures seem reasonable for evaluating theories.
Loop of loops
Where a simple causal loop (for example “A causes A” or perhaps “A causes B and B causes A”) may appear to be a tautology and so not an appropriate and falsifiable part of a theory (Popper, 2002), it is worth noting that having multiple interconnected simple loops is a different situation. With multiple measurable and falsifiable propositions, we have a valid theoretical model (Priem & Butler, 2001). This kind of structure is seen in Figure 4 (Newton’s Second Law) where three “dyad” loops (each containing two concepts) are connected in an overarching “loop of loops” where each concept is a leverage point at the intersection of two loops.
Because we may reasonably expect theories of the social/behavioral sciences to contain more concepts (as social situations are more complex), it may be interesting to explore and create theories of that structure with more concepts, abstractly represented in Figure 8.
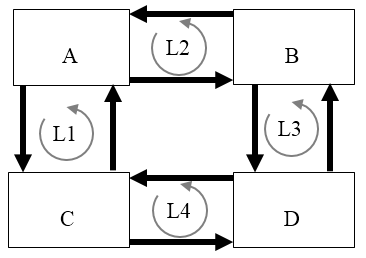
Figure 8 A loop of loops containing four dyad loops connected in a larger loop
Larger theories (with more concepts/boxes) are possible when adding more loop dyads creating a larger loop of loops. Again, this is a tentative hypothesis and suggests the opportunity for future research.
Perhaps the most important area for future research is to shine a light on the general assumption presented here of the usefulness of the theories under analysis. The present measures will have greater validity when they are more closely correlated with some objective and rigorous evaluation of that usefulness; perhaps quantified by the number of accurate predictions.
Future studies might also expand the analysis to include more theories overall; and, more specifically, more histories of theories from a broader range of fields. Additionally, future studies should investigate theories of greater complexity. Future studies might consider a range of theories with a variety of loops structures as they are applied in practice over an extended span of time. For example, one set of public service agencies might apply theories of change that are relevant to their missions, but have no loops, while another set of similar agencies apply theories of change which include many loops and leverage points. Alternatively, some organizations providing counseling services might use practices based on theories with few or no loops while another set of organizations provide services based on theories containing multiple loops. The differences in cases may prove rather illuminating provided there is substantive differences in the actual practices followed by those organizations; and, that those practices are clearly based on the theories.
As this is a preliminary exploration, limits of space, time, and other resources means that there are many areas and ideas that are not covered here, that could (and should) be studied in future research.
The notion of “coupled” systems could be explored because, in contrast to the present analysis of relatively isolated systems, “In many social systems the micro, meso and macro level dynamics are coupled, meaning that they cannot be studied or modified in isolation” (Johnson, Fortune, & Bromley, 2017). Future research might also consider the stability of systems (cf. Umpleby, 2018) based on the number and/or ratio of positive and negative loops, in addition to the openness of the system (or systems—linking conceptual, biological, and others). Indeed, having in mind a kind of “template” of loops may help to integrate/synthesize theories from disparate fields to generate theories that are more useful still.
Another direction for future research would be to consider whether the conceptual system is decomposable or not—including the notion of top down (or holographic) feedback (cf. Diniz & Handy, 2004) as well. Indeed, a very wide range of concepts from cybernetics and systems thinking may be researched for their relevance to conceptual systems (e.g., feedback, feed-forward, self-organization, recursions, reflection). It may also be considered how a complex social system may include multiple interwoven levels (Wallis, 2020d) suggesting a highly complex web between physical, biological, and conceptual systems.
The above results also suggest a balancing perspective to Ashby’s so-called ‘law’ of requisite complexity. Instead of looking merely at “how many” components are in a system, as Ashby might, the present paper suggests looking at the number and direction of loops within a conceptual system as a way to evaluate the quality of that conceptual system for education and practice in pursuit of understanding and resolving real physical world problems.
More speculatively, a better measure for the quality of a theory may not lie in the number of concepts or the number of loops. Rather, it may be in “how closed” the conceptual system is. That is to say, our “optimal” theory may be the one (with however many loops) where all concepts are included in loops, all loops are of the shortest path, and all loops have positive and negative balance, and all loops are connected with leverage points. This may be understood as a SOCS version of thermodynamic systems in the physical world and how they might be better understood by exploring flows of information and energy. Additional research would certainly lead to interesting insights in this area (cf. McKelvey, 2004). It may be, as suggested in a response to Roth (2019), that “Those [conceptual systems] with higher levels of structure are more open to data but less open to changes in conceptual components. Those with lower levels of structure are more closed to data but more open to changes in conceptual components” (Wallis, 2020a: 180).
Future philosophical exploration might consider how this kind of approach might change the way we think about “truth” when “usefulness” may be a more appropriate term. Because, “Systems sciences defy classification as either epistemology or ontology. Rather, it is reminiscent of the Greek notion of gnosiology concerned with the holistic and integrative exploration of phenomena and events.” meanings (Laszlo & Laszlo, 2009: 7).
Conclusions
The present paper has investigated a small set of evolving theories found in physics and public health to find what measures of structure might indicate which theories are more useful in practical application. As a preliminary study, this paper has presented a set of measures that may be used for evaluating the potential usefulness of theories; thus pointing a structural path for improving them. The limited sample size and the exploratory nature of this study limits the certainty of the conclusions that may be drawn. We are closer to the start of this area of study than the end.
This paper has achieved its purpose of conducting a preliminary exploration of causal structures of conceptual loops. And, in doing so, answer the research question of how we might more rigorously and objectively evaluate the conceptual loops presented in theories and models. By better understanding loop structures in theories, we may now reasonably expect to be able to build better theories; and, importantly, understand how much knowledge they hold and so make better decisions around the need for additional research or advancing toward action.
Reflecting on the comparison from the Glanville’s (2009) perspective comparing knowledge_of (representing the relatively limited knowledge of those with superficial understanding based on outside observation) and knowledge_for (representing deeper, more nuanced, and more useful knowledge for enabling change based on insights from the inside), the present paper suggests that the distinction is not a binary one. Rather, it seems we can evaluate our theories, regardless of their origin, according to their structure to determine the potential usefulness in practical application. Theories on the knowledge_of end of the scale will have lower scores of IPA’s Complexity and Systemicity, DIDO/MIMO, along with lower IPAx scores for loops and inclusions.
The research question for this paper asked: How might we more rigorously evaluate loops presented in theories to support our ability to develop theories that are more useful in practical application? This is important because, without a rigorous, objective approach to improving our theories, we risk developing overly simplistic theories that merely reinforce our biases.
This paper has answered the research question by using multiple methods to evaluate the structure of theories as they evolved from lesser to greater usefulness. Those methods include existing/proven methods such as IPA, along with suggested measure including the enumeration of conceptual loops which had been suggested, but not previously proven, to be useful for evaluating theories as a way to measure the potential usefulness of theories from a structural perspective. The results seem to correlate, showing that measuring the number and structure of conceptual loops within theories does indeed provide a useful tool for evaluating the potential usefulness of conceptual systems such as theories and models.
This is important for researchers, professors, and practitioners because they can use these measurements of structure (including conceptual loops) to show the validity of theories with greater confidence, objectivity, and rigor. That means professors can (and should) choose to teach theories that score higher on one or more of these measures. Practitioners can (and should) have their practices informed by theories with higher scores. Similarly, practitioners involved in strategic planning activities should encourage their clients to develop knowledge maps, theories of change, and similar representations of knowledge that have higher scores. For researchers (including students), the present results are also important because they suggest a path for more rapidly improving theories. For an abstract example, a researcher may begin by conducting a literature review on some topic of interest. And, finding a theory which contains few or no loops, can focus his or her research efforts on finding those causal connections that will “close the loop” and so develop a theory with more loops. And, more generally, researchers can (and should) develop theories with higher scores if they wish those theories to be more useful in practical application.
It should be noted that the present study is limited because it is focused only on causal relationships. It may be that there are a range of qualitative measures of those connections which may provide useful insights into structure. However, it should be understood, that each of those qualitative perspectives comes with a set of assumptions that must also be addressed—potentially leading to an infinite regress without a helpful conclusion.
While the focus of this paper has been on structure, it should also be noted that We gain greater confidence in the usefulness of our theories when they are supported by more qualitative and quantitative empirical data and when the theory is supported by a consensus of rational opinion across the field and perhaps beyond (Senge & Forrester, 1980). In short, knowledge is most useful in practical application when theories are supported on three dimensions of data (quantity and quality), relevance (to a broader range of stakeholders), and structure (Wright & Wallis, 2019). Improving theory on those three dimensions provides a guide to researchers who may want to “build” a “science accelerator” in their institutions to more rapidly advance their field of study for the benefit of all.
References
Appelbaum, R. P. (1970). Theories of Social Change. Chicago: Markham.
Bakker, J. I. H. (2011). North Central Sociological Association Presidential Address: Pragmatic Sociology: Healing the Discipline. Sociological Focus, 44(3), 167-183.
Beaulieu-B, P., & Dufort, P. (2017). Introduction: Revolution in Military Epistemology. Journal of Military and Strategic Studies, 17(4).
Bryson, J. M., Ackermann, F., & Eden, C. (2016). Discovering collaborative advantage: the contributions of goal categories and visual strategy mapping. Public Administration Review, 76(6), 912-925.
Bureš, V. (2017). A Method for Simplification of Complex Group Causal Loop Diagrams Based on Endogenisation, Encapsulation and Order-Oriented Reduction. Systems, 5(3), 46.
Burrell, G. (1997). Pandemonium: Towards a Retro-Organizational Theory. Thousand Oaks, California: Sage.
Chilisa, B., Major, T. E., Gaotlhobogwe, M., & Mokgolodi, H. (2015). Decolonizing and indigenizing evaluation practice in Africa: toward African relational evaluation approaches. Canadian Journal of Program Evaluation, 30(3).
Deegan, M. (2011). Using Causal Maps to Analyze Policy Complexity and Intergovernmental Coordination: An empirical study of floodplain management recommendations. Paper presented at the System Dynamics Society Conference 2011.
Diniz, L., & Handy, F. (2004). Holographic Structures Creating Dynamic Governance for NGOs.
Disessa, A. A. (2002). Why “conceptual ecology” is a good idea Reconsidering conceptual change: Issues in theory and practice (pp. 28-60): Springer.
Duggan, J., & Oliva, R. (2013). Methods for identifying structural dominance.
Friendshuh, L., & Troncale, L. (2012). SoSPT 1.: Identifying fundamental systems processes for a general theory of systems. Paper presented at the International Society for Systems Sciences (ISSS), San Jose, California, USA.
Glanville, R. (2009). A (cybernetic) musing: Design and cybernetics. Cybernetics and Human Knowing, 16(3-4), 175-186.
Gray, S. A., Zanre, E., & Gray, S. (2014). Fuzzy cognitive maps as representations of mental models and group beliefs Fuzzy cognitive maps for applied sciences and engineering (pp. 29-48): Springer.
Hayward, J., & Roach, P. A. (2017). Newton's laws as an interpretive framework in system dynamics. System Dynamics Review, 33(3-4), 183-218.
Hovorka, D. S., Birt, J., Larsen, K. R., & Finnie, G. (2012). Visualizing the core-periphery distinction in theory domains. Paper presented at the ACIS 2012: Location, location, location: Proceedings of the 23rd Australasian Conference on Information Systems 2012.
Johnson, J., Fortune, J., & Bromley, J. (2017). Systems, networks, and policy Non-Equilibrium Social Science and Policy (pp. 111-134): Springer, Cham.
Kampmann, C. E. (2012). Feedback loop gains and system behavior (1996). System Dynamics Review, 28(4), 370-395.
Kuhn, T. (1970). The Structure of Scientific Revolutions (2 ed.). Chicago: The University of Chicago Press.
Laszlo, A., & Laszlo, E. (2009). The systems sciences in service of humanity. Systems Science and Cybernetics-Volume II, 32.
Ledoux, L. (2012). Philosophy: Today’s manager’s best friend? Philosophy of Management, 11(3), 11–26.
Lewis, M. W., & Kelemen, M. L. (2002). Multiparadigm inquiry: Exploring organizational pluralism and paradox. Human Relations, 55(2), 251-275.
Light, P. C. (2016). Vision + Action = Faithful execution: Why government daydreams and how to stop the cascade of breakdowns that now haunts it. . Political Science and Politics, 49(1), 5-26.
Lipton, P., & Thompson, N. (1988). Comparative psychology and the recursive structure of filter explanations. International Journal of Comparative Psychology.
McGlashan, J., Johnstone, M., Creighton, D., de la Haye, K., & Allender, S. (2016). Quantifying a systems map: network analysis of a childhood obesity causal loop diagram. PloS one, 11(10), e0165459.
McKelvey, B. (2004). Toward a 0th law of thermodynamics: Order-creation complexity dynamics from physics and biology to bioeconomics. Journal of Bioeconomics, 6(1), 65-96.
Meadows, D. (1999). Leverage points: Places to intervene in a system, link.
Newell, W. H. (2007). Decision making in interdisciplinary studies. Public Administration and Public Policy, 123, 245.
Novak, J. D. (2002). Meaningful learning: The essential factor for conceptual change in limited or inappropriate propositional hierarchies leading to empowerment of learners. Science education, 86(4), 548-571.
Novak, J. D. (2010). Learning, creating, and using knowledge: Concept maps as facilitative tools in schools and corporations. Journal of e-Learning and Knowledge Society, 6(3), 21-30.
Oliva, R. (2004). Model structure analysis through graph theory: partition heuristics and feedback structure decomposition. System Dynamics Review: The Journal of the System Dynamics Society, 20(4), 313-336.
Oliva, R. (2015). Linking structure to behavior using eigenvalue elasticity analysis. Analytical methods for dynamics modelers, 207-239.
Pearl, J. (2000). Causality: Models, reasoning, and inference. New York: Cambridge University Press.
Phillips, S., & Wilson, W. H. (2014). A category theory explanation for systematicity: Universal constructions. The architecture of cognition: Rethinking Fodor and Pylyshyn's systematicity challenge, 227-249.
Popper, K. (2002). The logic of scientific discovery (K. Popper, J. Freed, & L. Freed, Trans.). New York: Routledge Classics.
Priem, R. L., & Butler, J. E. (2001). Tautology in the resource-based view and the implications of externally determined resource value: Further comments. Academy of Management review, 26(1), 57-66.
Roth, S. (2019). The open theory and its enemy: Implicit moralization as epistemological obstacle for general systems theory. Systems Research and Behavioral Science, 36(3), 281-288.
Russom, P. (2011). Big data analytics. TDWI best practices report, fourth quarter, 19(4), 1-34.
Saleh, M., Oliva, R., Kampmann, C. E., & Davidsen, P. I. (2010). A comprehensive analytical approach for policy analysis of system dynamics models. European Journal of Operational Research, 203(3), 673-683.
Schwaninger, M. (2011). System dynamics in the evolution of the systems approach. Complex Systems in Finance and Econometrics, 753-766.
Schwaninger, M. (2015). Model-based Management: A cybernetic concept. Systems Research and Behavioral Science, 32(6), 564-578.
Senge, P., & Forrester, J. W. (1980). Tests for building confidence in system dynamics models. System dynamics, TIMS studies in management sciences, 14, 209-228.
Senge, P., Kleiner, K., Roberts, S., Ross, R. B., & Smith, B. J. (1994). The Fifth Discipline Fieldbook: Strategies and Tools for Building a Learning Organization. New York: Currency Doubleday.
Sevaldson, B. (2011). GIGA-Mapping: Visualization for complexity and systems thinking in design. Nordes(4).
Sloman, S. A., & Hagmayer, Y. (2006). The causal psycho-logic of choice. Trends in Cognitive Sciences, 10(9), 407-412.
Sterman, J. D. (2012). Sustaining sustainability: creating a systems science in a fragmented academy and polarized world Sustainability science (pp. 21-58): Springer.
Stinchcombe, A. L. (1987). Constructing social theories. Chicago: University of Chicago Press.
Stinner, A. (1994). The story of force: from Aristotle to Einstein. Physics education, 29(2), 77.
Suedfeld, P. (2010). The cognitive processing of politics and politicians: Archival studies of conceptual and integrative complexity. Journal of personality, 78(6), 1669-1702.
Suedfeld, P., & Rank, A. D. (1976). Revolutionary leaders: Long-term success as a function of changes in conceptual complexity. Journal of Personality and Social Psychology, 34(2), 169-178.
Suedfeld, P., & Tetlock, P. (1977). Integrative complexity of communications in international crises. Journal of conflict resolution, 21(1), 169-184.
Suedfeld, P., Tetlock, P. E., & Streufert, S. (1992). Conceptual/integrative complexity. In C. P. Smith (Ed.), Handbook of Thematic Content Analysis (pp. 393-400). New York: Cambridge University Press.
Sweeney, L. B., & Sterman, J. D. (2007). Thinking about systems: Student and teacher conceptions of natural and social systems. System Dynamics Review: The Journal of the System Dynamics Society, 23(2-3), 285-311.
Umpleby, S. (2018). Identifying stability or instability in economic systems: Circular and linear analyses of financial crises. Financial University under the Government of the Russian Federation.
Umpleby, S., Wu, X.-h., & Hughes, E. (2017). Advances in Cybernetics Provide a Foundation for the Future. International Journal of Systems and Society (IJSS), 4(1), 29-36.
Van de Ven, A. H. (2007). Engaged scholarship: A guide for organizational and social research. New York: Oxford University Press.
Vemuri, P., & Bellinger, G. (2017). Examining the use of systemic approach for adoption of systems thinking in organizations. Systems, 5(3), 43.
Wakeland, W., & Medina, U. E. (2010). Comparing discrete simulation and system dynamics: Modeling an anti-insurgency influence operation.
Wallis, S. E. (2010). The structure of theory and the structure of scientific revolutions: What constitutes an advance in theory? In S. E. Wallis (Ed.), Cybernetics and systems theory in management: Views, tools, and advancements (pp. 151-174). Hershey, PA: IGI Global.
Wallis, S. E. (2011). Avoiding Policy Failure: A Workable Approach. Litchfield Park, AZ: Emergent Publications.
Wallis, S. E. (2014a). Abstraction and insight: Building better conceptual systems to support more effective social change. Foundations of Science, 19(4), 353-362. doi:10.1007/s10699-014-9359-x
Wallis, S. E. (2014b). Existing and emerging methods for integrating theories within and between disciplines. Organizational Transformation and Social Change, 11(1), 3-24.
Wallis, S. E. (2015a). Are theories of conflict improving? Using propositional analysis to determine the structure of conflict theories over the course of a century. Emergence: Complexity and Organization, 17(4), 1-17.
Wallis, S. E. (2015b). Integrative Propositional Analysis: A new quantitative method for evaluating theories in psychology. Review of General Psychology, 19(3), 365-380.
Wallis, S. E. (2016a). The science of conceptual systems: A progress report. Foundations of Science, 21(4), 579–602.
Wallis, S. E. (2016b). Structures of logic in policy and theory: Identifying sub-systemic bricks for investigating, building, and understanding conceptual systems. Foundations of Science, 20(3), 213-231.
Wallis, S. E. (2018, July 22-27). Actionable knowledge mapping to accelerate interdisciplinary collaborations for research and practice. Paper presented at the International Society for the Systems Sciences (ISSS), Corvallis, OR.
Wallis, S. E. (2019). Improving our theory of evaluation through an African-made process: An ubuntu answer to the decolonizing question. Administratio Publica, 27(4).
Wallis, S. E. (2020a). Commentary on Roth: Adding a conceptual systems perspective. Systems Research and Behavioral Science, 37(1), 178-181.
Wallis, S. E. (2020b). Integrative Propositional Analysis for Developing Capacity in an Academic Research Institution by Improving Strategic Planning. Systems Research and Behavioral Science, 37(1), 56-67.
Wallis, S. E. (2020c). The missing piece of the integrative studies puzzle. Interdisciplinary Science Reviews, 44(3-4).
Wallis, S. E. (2020d). Understanding and improving the usefulness of conceptual systems: An IPA based perspective on levels of structure and emergence Forthcoming.
Wallis, S. E., & Valentinov, V. (2016a). The imperviance of conceptual systems: Cognitive and moral aspects. Kybernetes, 45(9).
Wallis, S. E., & Valentinov, V. (2016b). A limit to our thinking and some unanticipated moral consequences: A science of conceptual systems perspective with some potential solutions. Systemic Practice and Action Research, 30(2), 103-116.
Wallis, S. E., & Valentinov, V. (2017). What Is Sustainable Theory? A Luhmannian Perspective on the Science of Conceptual Systems. Foundations of Science, 22(4), 733-747. doi:10.1007/s10699-016-9496-5
Wallis, S. E., & Wright, B. (2015, March 4-6). Strategic Knowledge Mapping: The Co-creation of Useful Knowledge. Paper presented at the Association for Business Simulation and Experiential Learning (ABSEL) 42nd annual conference, Las Vegas, CA.
Wallis, S. E., & Wright, B. (2019). Integrative propositional analysis for understanding and reducing poverty. Kybernetes, 48(6), 1264-1277.
Wamba, S. F., Akter, S., Edwards, A., Chopin, G., & Gnanzou, D. (2015). How ‘big data’can make big impact: Findings from a systematic review and a longitudinal case study. International Journal of Production Economics, 165, 234-246.
Weick, K. E. (1989). Theory construction as disciplined imagination. Academy of Management review, 14(4), 516-531.
Wong, E. M., Ormiston, M. E., & Tetlock, P. E. (2011). The Effects of Top Management Team Integrative Complexity and Decentralized Decision Making on Corporate Social Performance. Academy of Management Journal, 54(6), 1207-1228.
Wright, B., & Wallis, S. E. (2019). Practical Mapping for Applied Research and Program Evaluation. Thousand Oaks, CA: SAGE.