Chapter 12: Orthogonality—Developing a Structural/Perspectival Approach for Improving Theoretical Models
Wallis, S. E. (2020). Orthogonality: Developing a structural/perspectival approach for improving theoretical models. Systems Research and Behavioral Science, 37(2), 345-359.
My thanks to the two anonymous reviewers whose comments and suggestions led to a much improved paper. Any and all remaining problems remain my own.
Abstract
In order to create more useful theories we must attempt to choose better concepts (variables). Although we may strive to identify “independent” variables, that effort is problematic because we live in a world where everything is connected; also, attempting to obtain even nominally independent variables may require sophisticated analytical methodologies available only to well-funded researchers and practitioners. To help resolve those problems, and so provide an improved path for developing more useful theories, we explore the notion of orthogonality as a tool for rethinking concepts in a theory, from a structural perspective, in a way that clarifies research opportunities (from a data perspective) and clarifies situational/theoretical perspectives (from a relevance perspective).
Introduction
In science, understood as a process (Hull, 1988), key tasks include gathering data (through research and practice), building theory, and communicating the results to others. Within the social/behavioral sciences there are effective/rigorous guides for conducting research (cf. Argyris, Putnam, & Smith, 1985; Bentz & Shapiro, 1998; Charmaz, 2006; Checkland, 2000; Yin, 2011), engaging in ethical practice (cf. Hammersley, 2003), and communicating the results in peer-reviewed journals (cf. Armstrong, 1997).
For building theories (as a form of knowledge) that are more useful in practical application for reaching goals, it is helpful to understand theories as systems of concepts (cf. Umpleby, 1997), having a kind of causal logic structure. Recent research focused on that structural perspective identifies new paths for rigorously evaluating and improving theories (Wallis, 2016a). Approaches to evaluating structure include measures of Systematicity (cf. Gentner & Toupin, 1986), Integrative Complexity (cf. Suedfeld, Tetlock, & Streufert, 1992), Integrative Propositional Analysis (cf. Wallis, 2016a; Wallis & Wright, 2019), loops (Wallis, 2019), abstractions (Wallis, 2014), and sub-structures (Wallis, 2016b).
Theories are more useful for enabling successful decisions and actions when they have more supporting data, greater meaning or relevance to the stakeholders and their situation, and higher levels of causal logic structure (Wright & Wallis, 2019). While appreciating the importance of data and relevance, in this paper we focus on that structural perspective to explore and develop an approach to evaluating and improving theories based on the concept of “orthogonality.” Briefly, as this will be explored in greater depth below, orthogonality is an expression of difference between two concepts specifically with respect to their causal relationships representing some transformation (not merely that they are different).
For a simple example, Figure 1 abstractly represents two concepts (A and B) that, together, cause change in a third concept (C). The extent to which A and B are uncorrelated reflects, to some extent, our understanding of how change occurs in C. Both (and perhaps more) are required for change in C.
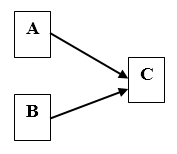
Figure 1 Simple, abstract, causal theory (boxes represent concepts/variables, arrows represent causal relationships)
Alternatively, if there is some correlation between A and B (represented in Figure 2) our understanding is not so clear. Graphically, that correlation may be represented by overlapping boxes (Figure 2) reflecting some commonality between them.

Figure 2 Overlap between concepts reducing clarity of understanding
Individual and teams are highly effective at identifying things, applying labels, and reaching conclusions. However, this kind of process often results in a pretense of knowledge with accompanying confusion, poor policy choices, and social turmoil (Hayek, 1974) rather than generating more useful patterns of understandings (Lissack, 2019). Even when this is done in the context of academic research, this process has led to fragmentation and confusion rather than clear advances in science and practice (cf. Newell, 2007).
Wallis (2016a) has surfaced this concern recently, suggesting that “If we can create new rules for evaluating theories based on the orthogonality of causal inputs (and outputs), we will have made a very large step forward in understanding how to create more useful theories” (p. 594). However, it seems that we have no great understanding of orthogonality—no way to say with any level of objectivity or rigorous process that pairs of concepts are “more orthogonal” than another so there is no “compass” to guide the theory builder.
This is important because orthogonality is one way we understand things as being different, yet connected. As such, it is a critical part of our understanding our world of things that are “differentiable yet inseparable” (Zude & Yolles, 2006).
If we can find better paths to evaluating and building theories, we may be able to more easily to determine the most useful theories for teaching, publication, and application. Finding such gaps in our theories to identify opportunities for improved research and practice, this structural approach to orthogonality in theory building, may serve as a science accelerator with attendant benefits for humanity.
Definitions
Before proceeding to greater depths, some relevant definitions are in order.
Theory
Generally, we may think of a theory as a system because:
…a system is a complex object whose parts or components are held together by bonds of some kind. These bonds are logical in the case of a conceptual system, such as a theory; and they are material in the case of a concrete system, such as an atom, cell, immune system, family, or hospital. The collection of all such relations among a system’s constituents is its structure (or organization, or architecture). (Bunge, 2004: 188).
Therefore, for this paper, a theory may be understood as a system of concepts (variables, categories, or abstractions of the real world) linked by causal connections. Other conceptual systems are models, theoretical models, mental models, policy models, metatheories, theories of the middle range, policy theories, sets of hypotheses, or any other similar thing which may be used as a framework of knowledge for understanding and engaging the world (Wallis, 2016a). For our purposes, a better theory is one that is more useful in practical application for reaching specified goals. Through primary and secondary research, such theories are created by building on higher levels of supporting data, greater relevance to users, and more systemic structure (Wright & Wallis, 2019). One approach to understanding and improving structure is orthogonality.
Orthogonality
For a brief overview (we will go into greater depth later) the term orthogonal is used in a rather imprecise, casual, and often incorrect way to present something that is “different.” For example, (Peters, 2019) describes organizations (e.g., military) as having a dominant culture (e.g., work ethic) while also having sub-cultures (e.g., slacker) that are subversive to the dominant culture. He sees the difference between those cultures as orthogonal. On the surface, that use of the term seems to imply that the two cultures are “very different.” Such is not a highly useful distinction. After all, a star in the sky is very different from a set of accounting principles used in a business; yet, the two would not (or should not) be considered orthogonal unless someone were able to show that the two are causal and necessary for some resulting phenomenon.
If Peters were to see the different cultures as combining to create something new (e.g., the conflict between them) then the cultures might be considered (to some extent) orthogonal. Instead, his discussion was on the differences between them as a source of different perspectives and the desired state of having cultural commonality or uniformity within an institution (Peters, 2019). Instead, because culture may include more things than perspectives (e.g., people, artefacts, and activities) there may be considerable overlap between the many aspects of the two cultures thus limiting our understanding of the situation. A racist may perceive substantial differences between individuals of different skin color while a psychologist may perceive few or none.
Here, we want to avoid having “orthogonality” become synonymous with “different” and instead develop a perspective of orthogonality that seeks to understand two or more concepts that are different and causally interrelated in some way.
That dual perspective (à la Bateson, 1979) of difference and relationship gives us the opportunity to see our conceptual systems with greater clarity and so develop more useful theories.
In the academic world, a common way to understand differences between concepts in a theory is to identify them as independent variables. The importance of having variables be independent from one another is generally accepted in theory building (cf. Ahn, 1997). However, choosing independent variables or concepts is often difficult for scholars and practitioners, requiring statistical techniques such as the R-squared test which, although it is widely used, is often misused (Kvålseth, 1985).
So, even a comprehensive research project of vast scope (and cost) may not provide a highly useful reflection of reality. Also, such empirical approaches do not lend themselves to qualitative research or to the activities of politicians, managers, and others who must make decisions on a daily basis without having access to sufficient empirical data, statistical methodologies, or expert scholars. The difficulty is accentuated when conducting qualitative research and still greater when developing speculative theories because of the difficulty of intuitively choosing things that seem to be completely different in a world where everything seems to be connected.
Metaphorically, we might imagine designing a skyscraper where the plans describe clear differences between structural components but only vague descriptions of how they are to be assembled. Rather than placing girders at specific angles required to provide structural integrity, they end up instead being connected haphazardly; and, unable to support their own weight, collapse.
In short, to develop more useful theories (with better structure), we should better understand the orthogonality between concepts in each theory. And, importantly, the methods developed from that understanding should be accessible to a wide range of scholars and practitioners.
Steps to resolving the problems
The primary goal of this paper is to explore the meaning of orthogonality as it may be applied to understanding and improving conceptual systems such as theories. With that improved understanding, another goal of the present paper is to make it easier for scholars and practitioners (including emerging experts and citizen scientists) to advance or improve theory for practical application.
This is important for choosing concepts for theories that relate to real world phenomena because that process is often accompanied by a high level of ambiguity. “By ambiguity, I mean the coexistence of multiple interpretations of a phenomenon among reasonable people while there is not necessarily an easy way to choose between interpretations or eliminate some of them” (Dahler-Larsen, 2018: 7).
In the following section, we begin by briefly considering existing thinking on the closely related areas of causality and abstraction (understood as a kind of categorization) for building theory, then considering in some depth existing thinking on orthogonality from perspectives found in multiple fields. Next, we explore the implications of those perspectives on orthogonality as they may be applied to building theory. After that, we present a set of instructions for using orthogonality as a tool for theory building, and offer a range of questions and opportunities for continuing this stream of research.
Existing Thinking
Metaphorically, when building a theory, we are striving to assemble a panorama from a multitude of photographs. While it is possible to gain some kind of view from any combination of photographs, the best view is one where we are aware of (and deal appropriately with) gaps and overlaps among the individual photos.
It is not enough to ‘simply’ create a better panorama by including more photos (ending up with some sloppy bricolage); nor is it enough to create a better theory by including concepts. “Indeed, the art of dealing with the complicated and complex real world lies in knowing when to simplify and when, and how, to complicate” (Rogers, 2008: 30). In this section, to better understand that art, with an eye toward creating more of a science, we briefly review some existing thinking on concepts (or categories) and causality before touching on the idea of relevance and then taking a deeper dive into understanding the existing thinking around orthogonality from multiple fields.
Concepts and Categories
For our purposes, a concept (sometimes referred to as a category) is anything that can be named (e.g., atoms, cars, hats, planets, along with various activities and so on). The thing may be a concrete object in the real world or something more abstract such as “democracy.” Concepts are, by nature, abstractions.
Many terms have been used to identify such things including concept, category, aspect, vertex, variable, point, object, node, and so on. More philosophically, they may be referred to as “normal types” or “ideal types” (Fink, 2014). For the present paper we may use those terms interchangeably but will generally rely on the term “concept.”
Additionally, and importantly for our present discussion of orthogonality, each concept may have multiple sub-concepts in much the same way that a physical object has parts. For example, the concept of “productive worker” may be said to include sub-concepts of productivity and person.
While each concept is an abstraction, it is worth noting that each is at some level of abstraction. For example, apple trees, fruit trees, and trees represent three levels of abstraction where they (also understood as categories) may hold the same “things.” A theory will be more useful when its concepts are at a similar level of abstraction (Wallis, 2014) whether they are chosen from the start of a study or changed to be more similar as a result of developing the theory.
A theory that contains concepts of both “fruit” with “apples” may lead to confusion. For example, imagine someone asks you how many apples farmer Jane has available for sale that day. You call the farm and are told that there is one basket labeled “apples” containing ten items and another basket labeled “fruit” containing 10 items. There may be ten apples, there may be twenty… or somewhere in between.
Moving too far up some scale of abstraction may not be useful. A farmer, for example, might want to work at a level of abstraction where she categorizes “male cattle” and “female cattle” for the purposes of breeding, milking, and so on. If she were to categorize on a higher level, such as “animal,” the corral might be filled with all kinds of creatures—leading to pandemonium instead of a functional and productive farm.
While such concrete things are easy to differentiate in daily life, theories may contain concepts that are less clear, such as democracy or freedom. So, an important point to consider is that the concepts in a theory should be “mutually exclusive” in the sense that there should be no overlap between them. This reduces the chance of misunderstanding and confusion on the farm (this will be discussed in greater detail, and with fewer metaphors, below).
Another important point is that such abstractions of concepts are not known in advance. Instead, in qualitative research in the social/behavioral sciences, it is common to create themes or categories when coding and “clumping” qualitative data as those themes seem to emerge from the data as perceived by the researcher (cf. Goulding, 2002; Yin, 1984). In contrast, through history, some have attempted to create “perfect” or “ultimate” lists of concepts. However, they have not gained wide acceptance.
Just to briefly mention some examples from philosophy, Aristotle lists the following as the ten highest categories of things: “Substance (e.g., man, horse), Quantity (e.g., four-foot, five-foot), Quality (e.g., white, grammatical), Relation (e.g., double, half), Place (e.g., in the Lyceum, in the market-place), Date (e.g., yesterday, last year), Posture (e.g., is lying, is sitting), State (e.g., has shoes on, has armor on), Action (e.g., cutting, burning), Passion (e.g., being cut, being burned)” (link).
In contrast, Grossman identifies eight highest categories: “Individuals, Properties, Relations, Classes, Structures, Quantifiers, Facts, Negation” (link). A Hindu perspective suggests seven: “Ganeri: substance (dravya), quality (guṇa), motion or action (karma), universal (sāmānya), particularity or differentiator (viśeṣa), inherence (samavāya), and absence (abhāva)” (link).
Einstein might have said that there were two categories, matter and energy. And, those are essentially the same thing! Seven, eight, ten, two, one. We do not seem to have a definitive answer as to what that the appropriate number of categories actually is (or what those categories should be).
More pragmatically, for organizational improvement, it is common to use pre-determined categories for planning purposes. For example, the SWOT model (Dyson, 2004) suggests that there are four categories (Strengths, Weaknesses, Opportunities, Threats). The “business model canvas” (Joyce & Paquin, 2016) includes nine categories (Partners, Activities, Resources, Value propositions, Channels, Customer relationship, Customer segments, Costs, Revenues) while the “balanced scorecard” has eight (Kaplan & Norton, 1996). Four, eight, nine… which is the appropriate number, if any (and what should they be)?
As noted above, having overlaps between concepts/categories is more likely to engender confusion rather than understanding. So, considering categories is relevant for an orthogonal perspective because a problem arises when one thing shows up in two or more categories (concepts). For an example from the business world, consider the four categories of SWOT analysis. Imagine how something listed as a strength might have considerable overlap with something listed as an opportunity (e.g., a strength is our ability to find new customers while an opportunity is finding new customers). One might even list something like “intense focus on a task” as both a strength (ability to get work done) and a weakness (inability to shift focus when necessary). That overlap seems to provide at least a partial explanation, from a structural perspective, as to why SWOT has not proven highly useful for supporting successful business decisions (Hill & Westbrook, 1997). There is confusion on the farm due to insufficient differentiation between concepts.
Relevance / Meaning
While some perfect list of concepts may be someday found (a kind of theory of everything, or TOE), few scholars today are actually seeking such a thing. Instead, most would be satisfied to discover a set of concepts that help to understand and support a better path toward organizational improvement or improved national policy. That perspective suggests we should focus on identifying concepts that are relevant to each stakeholder’s specific situation. That is, those concepts that the stakeholders find most meaningful (Wright & Wallis, 2019). And, historically, that is what has been done to support successful decisions. For example, an engineer who is calculating the orbit for a communication satellite uses Newton’s laws of motion, ignoring Aristotle’s other categories (e.g., passion).
We agree with Westerhoff (2005) that there is no absolute, perfect, ultimate, final set of categories or concepts. Instead, the set of concepts within a theory should be chosen by the researcher—at least as a starting point. While every individual and group must have some perspective, a problem arises when different stakeholder groups build their understandings on concepts that have unarticulated overlaps (above section) and/or poorly understood causal connections between them (below section).
Causality
There has been so much written on the topic of causality and its relationships to developing useful theories that it hardly seems worth writing more (see especially Pearl, 2000). However, in conversations with colleagues we routinely hear that they deploy techniques for understanding a situation or supporting clients such as “concept mapping,” “bricolage,” “storytelling,” and “rich description” as substitutes for understanding causal relationships between concepts.
While those techniques are certainly useful to some extent (e.g., supporting generative conversations) research in the science of conceptual systems indicates that representations are more useful for understanding situations and enacting desired change when they (as theories, models, knowledge, etc.) include measurable concepts related with causal connections (Wallis, 2016a).
In short, it seems to be increasingly accepted that theories are more useful when they indicate causal relationships (cf. Ackermann & Eden, 2004; Bauer, Booth, & McGroarty-Torres, 2016; Bryson, Ackermann, Eden, & Finn, 2004; Bureš, 2017; Deegan, 2011; Goodier, Austin, Soetanto, & Dainty, 2010; McGlashan, Johnstone, Creighton, de la Haye, & Allender, 2016; Panetti, Parmentola, Wallis, & Ferretti, 2018; Pearl, 2000; Sloman & Hagmayer, 2006; Waldmann, Holyoak, & Fratianne, 1995).
Part of the reluctance by some to accept causal models may stem from past reliance on purely linear models (for example: resources > activities > results). Encouragingly, in the field of program evaluation (and quite possibly others), there seems to be an increasing dissatisfaction with purely linear models. There seems to be, instead, a growing realization that models with more complex causal interconnections between those concepts will provide a more useful representation of the real world and so be more useful for planning and evaluation (Rogers, 2008; Wright & Wallis, 2019). These nonlinear models would show many activities, each of which causes changes in each other, along with complex causal connections between resources and goals.
This perspective is generally accepted within the complexity sciences, where it is reasonably held that simple causal connections are suspect; the world is more complex than that. That is, for an abstract example, we would be suspicious of a simple claim that only A causes only B because such a claim would contradict the idea that the world is made of many complex causal interactions. While it may be difficult to unravel those connections, we believe that it is possible. To avoid making decisions (or taking action) based on causal relationships, therefore, is to invite poor results.
Although identifying causal connections may be difficult (Sprites, Glymour, & Scheines, 1993), the benefits are worth the effort because understanding causal relationships improves our actionable knowledge (Johnson-Laird, 1980) necessary for effective decision making (Sloman & Hagmayer, 2006) especially in business settings (Axelrod, 1976). Also, understanding causal relationships supports long-term learning in children (Bauer et al., 2016).
For creating diagrams, specifically knowledge maps, causal relationships are presented as arrows between concepts. Such causal connections are also referred to as edges, morphisms, links, and so on. For the present paper, we will generally refer to them as arrows or causal connections.
Orthogonality
To deepen the brief introduction to orthogonality presented in the introduction section, it seems interesting to note that the term is derived from the Latin “orthogonus” meaning “right angled,” orthogonal is “pertaining to or involving right angles” (from geometry) and (from statistics) “statistically independent” (OED, 2007: 2029). That is to say, when we are looking at two boxes (or independent variables) and their causal arrows pointing towards a third box (dependent variable), we are more certain that the resulting understanding is valid (and presumably useful) because those two causal variables are independent of one another.
An example from the field of psychology relates to models having been developed to describe three factors of behavior (Finkel, 2014) and the Big Five factors of personality (Saucier, 2002) where researchers understand that the greater degree of orthogonality, by which they mean independence between variables, the more valid the model and the more useful it may be for making predictions. However, the orthogonality of data is often difficult to justify on theoretical grounds (Mishler & Rose, 1997).
Although it may be challenging, in contemplating “how orthogonal” two concepts might be to one another, we push our thinking. And that is the stuff that scientific advances are made of.
Rethinking our assumptions is important for making progress because researchers of the social/behavioral sciences (as well as the humanities) are rarely in a position to conduct repeatable experiments under controlled situations. We, along with our students and clients living in a rich and complex world, require a more pragmatic guide for developing simple understandings into complex theories and eventually creating law-like conceptual structures. We need a deeper understanding—a “why” approach of logics that is different from yet related to a “what” approach of data. We must find a balance between the human desire for parsimony and the need to understand our complex world to reach challenging goals. In the world of policy implementation, there are simply too many variables in our world to completely make sense of it all and gain the policy results we expect (Goggin, 1986). And, variables that are important may not be accessible for measurement (Hayek, 1974).
A perspective from statistics is focused on finding variables that are independent or “uncorrelated” (Ahn, 1997). That is an important idea because it relates to the reliability of data in theory building as well as the construction of useful theories—based on “concatenated” logic structures (Wallis, 2016b). Briefly, a concatenated structure is one with more than one causal arrow pointing toward a concept from other concepts (Figure 1). While orthogonality between variables is a desirable goal variables of “constructs in the real world are rarely uncorrelated” (Ford, MacCallum, & Tait, 1986).
Sterner (2014) suggests that epistemology and ontology are orthogonal to one another. Importantly, he notes that orthogonality is different from opposition. That is, concepts which are orthogonal are 90 degrees apart, they are not opposites. He states, “Much needs to be done, though, before the idea of ‘concurrent but orthogonal’ can offer a full accounting of the conceptual structures underlying the debates over explanation” (p. 251). Lissack and Graber (2014) suggest that epistemology and ontology are not in opposition, rather they are orthogonal and congruent. Yet, in their explanation, they suggest that the division between the two is not so clear and that the activity around them may exist on some spectrum.
In this interconnected universe, no variables are truly independent. So, a better (or, at least an alternative) way to choose them might be to evaluate “how orthogonal” they are; and, for improving theory, continually strive to develop concepts within the context of a theory that are increasingly orthogonal.
Let us go back to a simpler perspective for clarity. In mathematics, an example of orthogonality may be found in any algebraic operation. For example, where A x B = C (or, more concretely, money in investments x rate of return = dividends). If A or B were reduced to zero, C would also be zero. So, A would be considered orthogonal to B. However, because A and C are both measures of money (investment and dividends), they may not be considered completely orthogonal.
A clearly non-orthogonal relationship is seen in additive operations where (for example) A + B = C (or, more concretely, (money received from investments + money received from paychecks = money in bank). A or B could be zero but C could still be non-zero).
For another example, if one were to say, “more human labor and more component parts both combine to create finished widgets” we could more easily see labor and parts as orthogonal to one another. Whatever it may be that we are measuring, the two measures are not the same thing. They are (in some sense) multiplicative instead of additive. There will be no finished widgets if either variable drops to zero. Or, from the perspective of Boolean logic, additive causal streams are “OR” operators while orthogonal ones are “AND” operators (my thanks for that insight to Stankovic, personal communication, email, 7/25/2017).
To summarize the key points of this section, in seeking to create more useful theories, concepts should be related to one another by causal connections, and should be relevant/meaningful to the users of the theory and their situation/context. Importantly, there should be no overlap between concepts (we will discuss this more below). In the following section, we conduct a deeper exploration into orthogonality to find out and clarify how an orthogonal perspective may be used for developing more useful theory.
Exploration
In creating models, it is important to consider how the constituent concepts are selected or understood within some context, and how they are differentiated, combined, and correlated (Gabora, Rosch, & Aerts, 2008) leading to a more useful model.
While orthogonality is (to some extent) used (and to some extent misused) in the literature of the social/behavioral sciences to describe relationships between concepts, it is generally ignored as a tool for evaluating our theories with any level of objectivity and so for improving them. That is, to create theory that is more useful in practical application. The process of striving towards orthogonality provides a way to re-think concepts and assumptions to bring new and better understanding to topics of study.
Ingo Pies and others use orthogonality to identify new directions of thinking to resolve conflict—to find win-win situations (Beckmann, Hielscher, & Pies, 2014; Hielscher, Pies, & Valentinov, 2012; Pies, 2016). For example, in the conflicting views/goals between environmentalists (seeking to preserve nature) and capitalists (seeking to exploit nature), an orthogonal position might be seen in the new goal of sustainability—something of interest to both sides. Their approach, combined with the systems-based approach presented in the present article, may prove a powerful tool for helping the world to better understand how to understand their world for mutual benefit instead of mutually destructive conflict.
Seabury (1991) notes that the process of abstraction involves identifying similarities and disregarding differences. For example, in developing laws of motion, Galileo learned to ignore the color of his spheres (Oh, 2014) to focus on the more relevant measurement of movement. In contrast, when looking at organizations, we may find ourselves looking at (for example) relationships between two different departments. When, in actuality, they may be abstracted in many alternative categories. To use such a broad description as “department” may disguise the few (yet important) differences while ignoring potentially confusing similarities. This orthogonal perspective provides a tool to help us differentiate those important details.
If we engage an orthogonal perspective “correctly” as we identify and clarify concepts for a theory, we will be ignoring (perhaps removing them from the theory, or re-combining them with other concepts in the theory) those concepts that are less orthogonal to one another and focusing on those concepts that are more orthogonal. For a practical example from gardening, both seeds and soil are made of physical matter. Yet, when creating a theory of gardening, and deciding which should be planted in the other, we focus on the differences between the two—the biological material of one and the nutrients of the other rather than construct a theory focused on how those two are both composed of matter.
While the orthogonality between concepts may seem clear within a simple example from gardening, it becomes devilishly difficult when we are examining a complex social topic such as economics. It may seem obvious that the concepts should relate to economic issues such as interest rates, employment rates, and so on. One thing seems certain; that to understand a more complex phenomena such as an economy, a theory will require more concepts. And, with a growing number of concepts, a greater probability of low orthogonality between some of the concepts.
In a universe where everything seems connected, we must ask if it is even possible for any two concepts is be independent. For example, looking at Ohms Law of electricity there are three concepts; each of those is dependent from (causally resulting from) the other two; each is what we call transformative or concatenated (Wallis, 2019). Because each concept/variable is transformed by every change in input from other concept/variables, it seems that they “behave” as if they were independent variables even though they are clearly interconnected when one views the complete model. That is, in an experiment, the data might show no correlation between the two “input” variables when viewed from the “perspective” of the output variable, suggesting a better term would be “interdependent variables.” Further exploration is beyond the scope of the present paper, but raises interesting possibilities for the philosophy of science.
Because everything is connected, there may be no such thing as perfect, ultimate, or “global” orthogonality. However, it seems useful to differentiate between things in the real world so it seems useful to understand that differentiation as a kind of “local orthogonality.” For example, “math” doesn’t care if a student balances an algebraic equation, but the professor can differentiate between right and wrong answers on the test. So, there can be learning and improvement.
Perspectival Orthogonality
Hypothetically, some ultimate list of concepts may be possible, when the topic is something at a similar “ultimate” level such as “reality” or perhaps “knowledge.” However, “The uncertainty principle states that in an effort to gain precision about individual parts of a system, researchers lose precision in their knowledge of the whole system. For example, researchers can measure the momentum of a particle or its position, but both variables cannot be measured at once.” (Monahan & Fisher, 2010: 360). That is to say, the researcher unavoidably interacts with the subject or topic of study. And, for our purpose, that interaction between observer and observed means that concepts will emerge and become part of the theory.
Therefore, while achieving global orthogonality seems impossible (or at least very unlikely), “perspectival orthogonality” still seems possible. And, a potentially useful notion provided that the conditions for finding orthogonality are effectively articulated.
For example, an ocean might be viewed as “raw material” to an uncaring industrialist, as a “subject” to an artist, “beauty” to vacationers, or a “preserve” to an environmentalist. Each perspective will have some orthogonal counterpart. Not only because of the perspective of the viewer, but also according to its use. So, while a shift in perspective may result in some concepts being removed (or included) to a theory, this is more about the relevance or meaningfulness of concepts within a theory according to different perspectives.
For a simple diagrammatic example we may consider a figure depicting two lines, intersecting at right angles (Figure 3). They are orthogonal—and serve as a graphical representation of two causal inputs that are orthogonal. Now, rotate the figure so that the two lines appear to be one. The perceived orthogonality is lost by a change in perspective. Or, for our purpose here, concepts that appear orthogonal in one theory may not appear orthogonal in another theory. The relevant context for concepts is the theory consisting of other concepts.

Figure 3 Shifting/alternative perspectives confounding understanding
In Figure 4, the center diagram (map) may represent a (presumably, for our purposes here) some optimal theory representing some part of reality. Rotating that view along an axis serves to cause an apparent increase in size of some concepts and a decrease in others as seen in the center map while rotating the figure in the other direction enhances the seeming importance of different concepts (the left and right hand diagrams of Figure 4). Taken further, when a map is rotated sufficiently, some concepts may (seemingly) completely disappear.
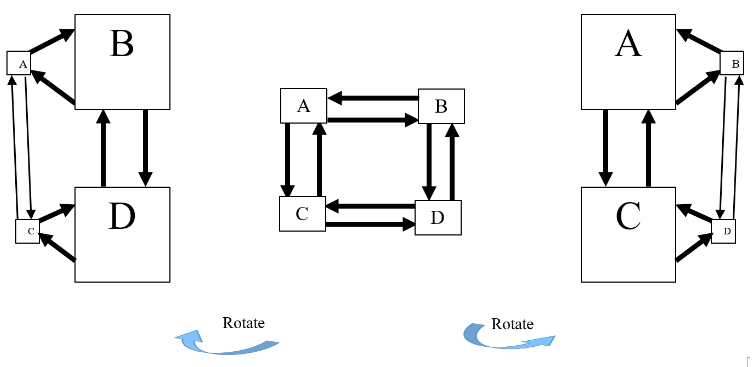
Figure 4 Shifting/alternative perspectives of an abstract theory
This graphical representation of perspective helps to show the view of some stakeholders that may be “stuck” in their own perspectives and unable to clearly perceive the larger picture. Such a perspective on perspectives may be extended to include changing views on causal relationships between concepts. Where, for example, one group might identify a causal relationship between two concepts, a second group believes that there is a relationship (perhaps that one influences the other) but not in a causal way, while a third group identifies no relationship at all. This perspectival approach suggests new directions for exploring and understanding how theories may be understood as having different “levels” depending on the perspective from which they are viewed or understood as “nested” within other theories. Such an exploration, however, is beyond the scope of the present paper.
While a perspectival approach opens the door for many alternative views, it should not be interpreted as a laissez-faire process. All parts of a model, from any perspective, should be supported by data (from quantitative and/or qualitative methods). Further, it is important to note that such a perspective is not the end point, once a perspective is found or chosen, it should be followed by orthogonal analysis from that perspective to identify/clarify directions for improving theories.
To summarize, there seem to be two unavoidable aspects that we should consider. The human perspective of choosing concepts that are relevant/meaningful to a topic/situation, and the structural perspective of comparing each concept with the others in the theory to improve orthogonality.
Historical Examples
About two thousand years ago, Plutarch articulated a theory of electrostatic attraction where rubbing a piece of amber was said to cause exhalations that pushed air that then pushed small objects (e.g., hair) toward the piece of amber (Wallis, 2010: 161). An orthogonal perspective would call attention to the overlap between the concepts of pushing air and pushing small objects; that is, both include pushing (which we may refer to as a sub-concept). Then, noting how such an overlap indicates an inappropriate lack of orthogonality between concepts in the theory, this perspective might suggest how the theory could be improved by removing one of those concepts. Such an insight might have inspired philosophers of the time to re-think the concepts of the theory and remove the concept of pushing air (for which they had no evidence anyway, only a strongly held assumption). And, as a result, the philosophers could have accelerated the development of science.
It is worth noting that the relationship noted above is a linear one (exhalations→pushing air→pushing small objects). In contrast, a more complex relationship may be seen in a theory of public health developed during an online conversation between novices and experts.
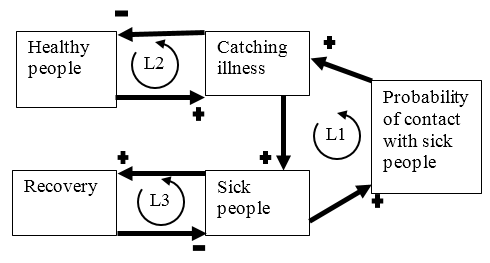
Figure 5 Theory of public health (Wallis, 2019), (boxes indicate concepts, straight arrows indicate causal connections, curved arrows indicate feedback loops).
An orthogonal perspective draws attention to the overlaps between the concepts within the theory. In Figure 5, note that the sub-concept “people” appears in three concepts. Also, note that the concepts of healthy people and sick people may be understood as having an overlap because “healthiness” and “sickness” may be understood as two ends of one scale. That provides an opportunity to re-think or re-consider the concepts; perhaps by combining those two into a single concept such as “level of health in society.”
This process may be challenging for some, testing deeply held beliefs and convenient observations. But those convenient measures of social phenomena may easily lead to problems such as economic tragedy (Hayek, 1974). However, we are not looking here for an approach that is comfortable or convenient. We are seeking to develop a method that is reasonably accessible to the average researcher for evaluating the level of orthogonality between concepts of a theory and then improve that orthogonality through carefully focused efforts. Challenge is to be expected and embraced.
Historically, this process could have been used to gain insight more rapidly and so accelerate the advance of the natural sciences. Now, it could be used to accelerate the advancement of the social sciences.
A recent interdisciplinary theory of poverty integrated concepts and causal connections from ten source theories (Wallis & Wright, 2019) included 37 concepts. Within those 37, a number were identified with potentially overlapping sub-concepts. For example, one concept “education, skills, resources” seems to overlap with other concepts that may be seen as resources such as “savings,” “social capital,” and “child care and early education.”
This kind of comparison suggests that the concepts should, in some sense, define each other. That is to say, when creating and/or evaluating a theory, we should compare each concept with the other concepts with an eye toward reducing and eventually eliminating the redundancies between sub-concepts. That, in turn, will support the development of theory that is more parsimonious and so more in line with Ockham’s razor (cf. Kelly, 2007; Kelly & Mayo-Wilson, 2012).
While re-thinking concepts and revising theories seems likely to support advancements in science, that approach could be more scientific (and so more useful) if we could evaluate theories based on some level of orthogonality between all the concepts within a theory. Such a “scale of orthogonality” would provide a useful metric; allowing scholars to compare theories with greater objectivity and so choose the most useful theories for teaching, research, and practical application.
Scale of Orthogonality
Another way to look at it is to ask how orthogonal are the concepts of a theory in relationship to one another? What is our measure of differentiation?
Can we develop a “scale of orthogonality?” Where concepts within a theory may be compared to show how orthogonal they are to one another? For example, “water” and “light” both support growth of plants. And, those may be seen as highly orthogonal to one another because removing either one would result in no plant growth. In contrast, if that growth was supported by both “fluorescent light” and “sun light” those two forms of light would not be quite so orthogonal to one another because both share a sub-concept (light).
Figure 6 provides an abstract example of a small theory containing three concepts (A, B, C), each with sub-concepts (represented by numbers). Where those sub-concepts are the same, they are represented by the same numbers and so may be said to have some amount of overlap.

Figure 6 Concepts and sub-concepts of a simple theory
This example serves to suggest that we can create a scale of orthogonality; at least in a very simple scale of high/medium/low. Future studies may develop a more sophisticated scale.
Future Directions
From this preliminary exploration, additional paths may be found. In this section, we will identify some of those paths for future research and consider some applications of orthogonality in practice.
In Practice
While some explanations of orthogonality may be complex and nuanced (if not occasionally confusing), some recommendations for using orthogonality in building theories are reasonably direct.
The first and easiest test for orthogonality between causally connected concepts in a theory is to conduct a thought experiment. Consider a conceptual structure where there are two or more input concepts and one output (e.g., Figure 6). If one of those input concepts is reduced to zero, then the resulting “output” concept should also go to zero, if the two inputs are orthogonal to one another. For example, if there is an assembly line where widgets are being made, the assembly requires both parts and labor. If one or the other is removed, the output of widgets will also drop to zero. If the construct passes this “zero-test,” it would seem that the inputs are orthogonal.
The second, more nuanced, approach is to identify all the concepts and all their sub-concepts within the theory. Then, re-think and revise them to reduce or eliminate overlaps. For this process, it may be useful to write concepts on large cards, then, on smaller cards or sticky notes attached to or adjacent to each large card, write the various sub-concepts. Then, it becomes a relatively straightforward process to identify the aspects in common across multiple concepts—and so identify what aspects each concept has in common and therefore how orthogonal the concepts are to one another.
Additionally, it is also suggested that collaboration between researchers may lead to more rapid and interesting evaluations of orthogonality. Existing methods for developing theory (e.g., grounded theory, qualitative research) are useful in that they generate many concepts (sometimes defined as categories, themes, etc.). The present paper suggests that those kinds of analyses should be followed by an analysis of the orthogonality between the concepts.
Rather than starting with chosen concepts, and deconstructing them into orthogonal parts (as in the above paragraph, this section), let’s return to categories (as discussed in a previous section); or, as they may also be understood, “classifications” (cf. Szostak, 2012). It may be a useful process to consider the concepts of a theory and ask if they may be placed into the same category/classification (e.g., both may be considered “activities”). If so, their orthogonality may be in question and some re-thinking may be indicated.
Again, the re-thinking depends in part on the level of analysis or level of abstraction of the concepts in the theory. So, it might make sense to include two activities if they pass the above zero-test. However, we should not rush to accept a pretense of orthogonality merely for the sake of convenience when re-thinking may lead to significantly useful insights.
Orthogonality may play a useful role in advancing public discourse around large and fuzzy concepts such as national “greatness” (cf. Darwish, Magdy, & Zanouda, 2017) or “transparency in government” (cf. Valentinov, Verschraegen, & Van Assche, 2019). Such notions often grab public attention and seem to become fixed in peoples’ minds. As such, some individuals may seem “impervious” to rational debate (Wallis & Valentinov, 2016) which may lead to conflicts between groups; each with their tightly held (yet large and fuzzy) assumptions. Utilizing the orthogonality perspective developed here, it may be possible to deconstruct and reconstruct such complex notions into their interrelated parts.
This orthogonal perspective suggests that some techniques (such as rich descriptions and concept mapping) may be more useful for surfacing insights than generating knowledge. So, we may consider them part of a two-phase process where such techniques are followed by an iterative process of cycling between structural development techniques. Generally, these structural approaches may be understood as IPAx (experimental techniques of the broader Integrative Propositional Analysis methodology) (Wallis, 2019). It is expected that orthogonality will be part of an iterative process, conducted in conjunction with other structural methods such as measures of systemic depth, conceptual breadth, loops (Wallis, 2019) and abstraction (Wallis, 2014) in addition to measures of data and stakeholder relevance (Wright & Wallis, 2019).
Future research
Ontologically, understanding what something “is” (or what dynamics are occurring) may seem to be a straightforward process of making an observation and applying a label. However, we can only gain clarity about what something is by understanding what it is and how it causes change. That distinction is what we are striving for in developing more useful theories from an orthogonal perspective.
This exploration has served to surface and develop some preliminary answers to important questions on building more useful theory. More effort is needed before the orthogonal approach is fully developed.
As discussed above, the importance of concatenated structures (e.g., Figure 1) has been established as an improvement over purely linear theories. However, linear theories may serve as a starting point for developing theories of greater systemic structure. When starting with a linear structure, it may be useful in some settings to brainstorm new concepts to add to the theory. In such situations, practitioners and researchers may want to use categories (as discussed above) to support the brainstorming process by purposefully seeking concepts from alternative categories. For example, if some existing theory has three concepts from the business model canvas (Joyce & Paquin, 2016) (e.g., partners, activities, resources), brainstorming might focus on finding concepts in other categories (e.g., value propositions, channels, customer relationship, customer segments, costs, revenues). That would help encourage theory builders to seek what is not there, rather than to repeatedly focus research efforts on what is already in the theory.
With the development of more useful theories, and the synthesis of theories from across and between disciplines, a door may be open for theories which identify recursive relationships between their topics (e.g., global poverty) and their observers (e.g., researchers).
On a deeper level, this orthogonal perspective gives rise to interesting questions around ontology. More specifically, the difference between fact and fiction. Generally, we like to see our theories supported by data. That indicates some relationship between the abstract concepts and the “real world.” Yet, it is possible to create a well-structured theory that is entirely fictitious. Indeed, every fiction may be seen as containing something of reality. Even a story about people flying through space faster than the speed of light (clearly a fiction) contains sub-concepts with a clear foundation in reality (people, space). Perhaps some exploration in this direction might yield interesting insights into the nature of reality—or at least our perceptions of “it.”
We anticipate that more structured models will lead to greater ability to solve problems. However, we must wonder if greater structure may also indicate tighter focus within a context? For example, grounded theory (cf. Charmaz, 2006) is claimed as a good tool for creating useful theory. However, grounded theory is very context dependent and so the theories/models created should not be considered generalizable. Will increased orthogonality support increased generalizability? A world of research is waiting. A few more questions to be answered are:
- Might we create a “periodic table” of theories based on their orthogonalities?
- What if we were to investigate the potential relationship between the orthogonality of theories and the unanticipated consequences of using those theories in practice?
- Is there a way to understand the relationships between concepts as having some orthogonal relationship between them such that they may appear causal to one viewer and non-causal (but somehow influential) to another?
- Can we explore how this kind of orthogonal perspective might be used to identify “missing pieces” of our theoretical puzzles (known unknowns and unknown unknowns)?
- How might the insights and methods presented here be integrated more concretely with those of Ingo Pies to create a more effective process for moving people toward cooperation rather than conflict?
Conclusion
It is worth noting that Ockham’s razor is often deployed to suggest that theories should be parsimonious—often interpreted to mean “small” or containing fewer variables or no more than are needed to reach a satisfactory explanation (Kelly, 2007). Unfortunately, we don’t know, a priori, how many concepts are needed. Orthogonality supports the development of parsimonious theories by providing a tool for comparing concepts and reducing or eliminating redundancies and clarifying gaps in our theories to more effectively focus research activity.
Lissack and Graber (2014) made interesting progress in their efforts to understand explanations that are sufficient to satisfy. However, we need to be pursuing a larger question. After all, theories of physics in ancient times seemed to satisfy. Yet, they were not highly useful in practical application: Aristotle’s theory of motion was not as useful as Newton’s. Instead, of satisfaction, we suggest that researchers and practitioners pursue usefulness in theories. As serious scholars, we should push ourselves, and each other, to create theories that are increasingly more useful in practical application; not simply good enough for publication.
In short, orthogonality is one way we understand things as being different, yet connected. As such, it is a critical part of our understanding the world. Importantly, while having a process for re-thinking concepts supports the development of theory, having a rigorous process suggests a more direct path, so that scholars may make progress more rapidly toward more useful theories.
The focus of the present paper has been mainly on improving theories of the social/behavioral sciences because they have the greatest opportunity for rapid advancement among the increasingly fragmented fields (Donaldson, 1995) before “paradigm wars” cause much greater decline in the perceived legitimacy of our scholarly efforts (McKelvey, 2002). However, it should also be noted that the natural sciences may also benefit from this emerging understanding of orthogonality.
Many forms of information and theory presentation (stories, slogans, etc.) create the pretense of knowledge (Hayek, 1974). Despite, (or because of) the limitations of our human minds, we would benefit from clear, rigorous, direct methods for advancing theory to support advances in practical application.
References
Ackermann, F., & Eden, C. (2004). Using causal mapping - individual and group, traditional and new. In M. Pidd (ed.), Systems Modeling: Theory and Practice (pp. 127-143). Chichester, UK: John Wiley & Sons.
Ahn, S. C. (1997). Orthogonality tests in linear models. Oxford Bulletin of Economics and Statistics, 59(1), 183-196.
Argyris, C., Putnam, R., & Smith, D. M. (1985). Action Science: Concepts, Methods, and Skills for Research and Intervention. San Francisco: Jossey-Bass.
Armstrong, J. S. (1997). Peer review for journals: Evidence on quality control, fairness, and innovation. Science and Engineering Ethics, 3, 63-84.
Axelrod, R. (1976). Structure of decision: The cognitive maps of political elites. Princeton: Princeton Universtiy Press.
Bateson, G. (1979). Mind in nature: A necessary unity. New York: Dutton.
Bauer, J. R., Booth, A. E., & McGroarty-Torres, K. (2016). Causally-rich group play: a powerful context for building preschoolers’ vocabulary. Frontiers in psychology, 7, 997.
Beckmann, M., Hielscher, S., & Pies, I. (2014). Commitment strategies for sustainability: how business firms can transform trade-offs into win–win outcomes. Business Strategy and the Environment, 23(1), 18-37.
Bentz, V. M., & Shapiro, J. J. (1998). Mindful inquiry in social research. Thousand Oaks, CA: Sage.
Bryson, J. M., Ackermann, F., Eden, C., & Finn, C. B. (2004). Visible thinking: Unlocking causal mapping for practical business results: John Wiley & Sons.
Bunge, M. (2004). How does it work? The search for explanatory mechanisms. Philosophy of the Social Sciences, 34(2), 182-210.
Bureš, V. (2017). A Method for Simplification of Complex Group Causal Loop Diagrams Based on Endogenisation, Encapsulation and Order-Oriented Reduction. Systems, 5(3), 46.
Charmaz, K. (2006). Constructing Grounded Theory: A Practical Guide through Qualitative Analysis. Thousand Oaks, CA: Sage.
Checkland, P. (2000). Soft systems methodology: a thirty year retrospective. Systems Research and Behavioral Science, 17(S1), S11-S58.
Dahler-Larsen, P. (2018). Theory-based evaluation meets ambiguity: The role of Janus variables. American Journal of Evaluation, 39(1), 6-23.
Darwish, K., Magdy, W., & Zanouda, T. (2017). Trump vs. Hillary: What went viral during the 2016 US presidential election. Paper presented at the International conference on social informatics.
Deegan, M. (2011). Using Causal Maps to Analyze Policy Complexity and Intergovernmental Coordination: An empirical study of floodplain management recommendations. Paper presented at the System Dynamics Society Conference 2011.
Donaldson, L. (1995). American Anti-Management Theories of Organization: A Critique of Paradigm Proliferation. New York: Cambridge University Press.
Dyson, R. G. (2004). Strategic development and SWOT analysis at the University of Warwick. European Journal of Operational Research, 152(3), 631-640.
Fink, G. (2014). Type building and mappings in organizational and cultural studies. European Journal of Cross-Cultural Competence and Management, 3(1), 93-100.
Finkel, E. J. (2014). The I3 model: Metatheory, theory, and evidence. Advances in experimental social psychology, 49, 1-104.
Ford, J. K., MacCallum, R. C., & Tait, M. (1986). The application of exploratory factor analysis in applied psychology: A critical review and analysis. Personnel psychology, 39(2), 291-314.
Gabora, L., Rosch, E., & Aerts, D. (2008). Toward an ecological theory of concepts. Ecological Psychology, 20(1), 84-116.
Gentner, D., & Toupin, C. (1986). Systematicity and surface similarity in the development of analogy. Cognitive science, 10(3), 277-300.
Goggin, M. L. (1986). The" too few cases/too many variables" problem in implementation research. Western Political Quarterly, 39(2), 328-347.
Goodier, C., Austin, S., Soetanto, R., & Dainty, A. (2010). Causal mapping and scenario building with multiple organisations. Futures, 42(3), 219-229.
Goulding, C. (2002). Grounded theory: A practical guide for management, business and market researchers. Thousand Oaks, CA: Sage.
Hammersley, M. (2003, 11-13 September 2003). Too good to be false? The ethics of belief and its implications for the evidence-based character of educational research, policymaking and practice. Paper presented at the British educational research association annual conference, Heriot Watt University, Edinburgh.
Hayek, F. (1974). A.(1989),'The pretense of knowledge'. American Economic Review, 79(6), 3-7.
Hielscher, S., Pies, I., & Valentinov, V. (2012). How to foster social progress: an ordonomic perspective on progressive institutional change. Journal of Economic Issues, 46(3), 779-798.
Hill, T., & Westbrook, R. (1997). SWOT analysis: It's time for a product recall. Long range planning, 30(1), 46-52.
Hull, D. L. (1988). Science as a process: An evolutionary account of the social and conceptual development of science. Chicago: University of Chicago Press.
Johnson-Laird, P. N. (1980). Mental models in cognitive science. Cognitive science, 4(1), 71-115.
Joyce, A., & Paquin, R. L. (2016). The triple layered business model canvas: A tool to design more sustainable business models. Journal of Cleaner Production, 135, 1474-1486.
Kaplan, R. S., & Norton, D. P. (1996). Using the balanced scorecard as a strategic management system: Harvard business review Boston.
Kelly, K. T. (2007). Simplicity, truth, and the unending game of science. In S. Bold, B. Löwe, T. Räsch, & J. v. Benthem (eds.), Foundations of the Formal Sciences V: Infinite Games (pp. 368). London: College Publications.
Kelly, K. T., & Mayo-Wilson, C. (2012). Causal conclusions that flip repeatedly and their justification. Retrieved from http://arxiv.org/ftp/arxiv/papers/1203/1203.3488.pdf
Kvålseth, T. O. (1985). Cautionary note about R 2. The American Statistician, 39(4), 279-285.
Lissack, M. (2019). Understanding Is a Design Problem: Cognizing from a Designerly Thinking Perspective. Part 1. She Ji: The Journal of Design, Economics, and Innovation, In press.
Lissack, M., & Graber, A. (2014). Modes of explanation: Affordances for action and prediction: Palgrave Macmillan.
McGlashan, J., Johnstone, M., Creighton, D., de la Haye, K., & Allender, S. (2016). Quantifying a systems map: network analysis of a childhood obesity causal loop diagram. PloS one, 11(10), e0165459.
McKelvey, B. (2002). Model-centered organization science epistemology. In J. A. C. Baum (Ed.), Blackwell's Companion to Organizations (pp. 752-780). Thousand Oaks, California: Sage.
Mishler, W., & Rose, R. (1997). Trust, distrust and skepticism: Popular evaluations of civil and political institutions in post-communist societies. The journal of politics, 59(02), 418-451.
Monahan, T., & Fisher, J. A. (2010). Benefits of ‘observer effects’: lessons from the field. Qualitative research, 10(3), 357-376.
Newell, W. H. (2007). Decision making in interdisciplinary studies. Public Administration and Public Policy, 123, 245.
OED. (Ed.) (2007) (6 ed., Vols. 2). Oxford: Oxford University Press.
Oh, J.-Y. (2014). Understanding natural science based on abductive inference: Continental drift. Foundations of Science, 19(2), 153-174.
Panetti, E., Parmentola, A., Wallis, S. E., & Ferretti, M. (2018). What drives technology transitions? An integration of different approaches within transition studies. Technology Analysis & Strategic Management, (online), 1-22. doi:10.1080/09537325.2018.1433295
Pearl, J. (2000). Causality: Models, reasoning, and inference. New York: Cambridge University Press.
Peters, B. G. (2019). Institutional theory in political science: The new institutionalism: Edward Elgar Publishing.
Pies, I. (2016). The ordonomic approach to order ethics Order Ethics: An Ethical Framework for the Social Market Economy (pp. 19-35): Springer.
Rogers, P. J. (2008). Using programme theory to evaluate complicated and complex aspects of interventions. Evaluation, 14(1), 29-48.
Saucier, G. (2002). Orthogonal markers for orthogonal factors: The case of the Big Five. Journal of Research in Personality, 36(1), 1-31.
Seabury, M. B. (1991). Critical thinking via the abstraction ladder. English Journal, 80(2), 44-49.
Sloman, S. A., & Hagmayer, Y. (2006). The causal psycho-logic of choice. Trends in Cognitive Sciences, 10(9), 407-412.
Sprites, P., Glymour, C., & Scheines, R. (1993). Causation, prediction and search (First, online ed.). Cambridge, MA: MIT Press.
Sterner, B. (2014). Explanation and pluralism Modes of Explanation (pp. 249-256): Springer.
Suedfeld, P., Tetlock, P. E., & Streufert, S. (1992). Conceptual/integrative complexity. In C. P. Smith (Ed.), Handbook of Thematic Content Analysis (pp. 393-400). New York: Cambridge University Press.
Szostak, R. (2012). Classifying relationships. Knowledge Organization, 39(3), 165-178.
Umpleby, S. (1997). Cybernetics of conceptual systems. Cybernetics & Systems, 28(8), 635-651.
Valentinov, V., Verschraegen, G., & Van Assche, K. (2019). The limits of transparency: A systems theory view. Systems Research and Behavioral Science.
Waldmann, M. R., Holyoak, K. J., & Fratianne, A. (1995). Causal models and the acquisition of category structure. Journal of Experimental Psychology, 124(2), 181-206.
Wallis, S. E. (2010). The structure of theory and the structure of scientific revolutions: What constitutes an advance in theory? In S. E. Wallis (Ed.), Cybernetics and systems theory in management: Views, tools, and advancements (pp. 151-174). Hershey, PA: IGI Global.
Wallis, S. E. (2014). Abstraction and insight: Building better conceptual systems to support more effective social change. Foundations of Science, 19(4), 353-362. doi:10.1007/s10699-014-9359-x
Wallis, S. E. (2016a). The science of conceptual systems: A progress report. Foundations of Science, 21(4), 579–602.
Wallis, S. E. (2016b). Structures of logic in policy and theory: Identifying sub-systemic bricks for investigating, building, and understanding conceptual systems. Foundations of Science, 20(3), 213-231.
Wallis, S. E. (2019). Learning to Map and Act Cybernetically Without Learning Cybernetics: **How Many Loops are Needed to Enable Effective Decisions and Actions? Paper presented at the American Society for Cybernetics, Vancouver, BC, Canada.
Wallis, S. E., & Valentinov, V. (2016). The imperviance of conceptual systems: Cognitive and moral aspects. Kybernetes, 45(9).
Wallis, S. E., & Wright, B. (2019). Integrative propositional analysis for understanding and reducing poverty. Kybernetes, In Press.
Westerhoff, J. (2005). Ontological categories: Their nature and significance.
Wright, B., & Wallis, S. E. (2019). Practical Mapping for Applied Research and Program Evaluation. Thousand Oaks, CA: SAGE.
Yin, R. K. (1984). Case Study Research: Design and Methods (Vol. 5). Beverly Hills, CA: Sage.
Yin, R. K. (2011). Applications of case study research: Sage.
Zude, Y., & Yolles, M. (2006, July, 2006). From Knowledge Cybernetics to Feng Shui. Paper presented at the International Society for the Systems Sciences, Sonoma State University, Rohnert Park, California.