NEURONAL NETS
Jack Cowan
Papers on large-scale nervous activity by McCulloch (and Pitts) with special reference to functional reliability
Selected Papers
| 1. How We Know Universal. The Perception of Auditory and Visual Forms. | Paper No. 75 |
| 2. The Statistical Organization of Nervous Activity. | Paper No. 80 |
| 3. A Recapitulation of the Theory, with a Forecast of Several Extensions. | Paper No. 81 |
| 4. The Stability of Biological Systems. | Paper No. 140 |
| 5. Agathe Tyche, of Nervous Nets - the Lucky Reckoners. | Paper No. 144 |
| 6. Anastomotic Nets Combating Noise. | Paper No. 160 |
| 7. Reliable System Using Unreliable Elements. | Paper No. 170 |
This group of papers covers various pieces of work by Warren McCulloch and collaborators, initially Walter Pitts, and later several persons, Manuel Blum, Leo Verbeek, Shmuel Winograd and myself. By 1946-7 McCulloch and Pitts were including considerations of stability of functioning under perturbations, i.e., functional reliability, in their theoretical formulations. This became one of the main themes of McCulloch’s work for the next 16 years, ending in 1963-4. By way of an introduction, it is perhaps worth giving a brief survey of the various problems confronted, and a short comment on recent developments in the theory of large scale nervous activity in neuronal nets, with special reference to the above problems.
Functional Reliability
McCulloch and Pitts were perhaps the first to raise the issue of functional reliability in their paper, How We Know Universal — The Perception of Auditory and Visual Forms, published in 1947 (Paper No. 75). In this paper, neuronal mechanisms for the recognition of forms were described, the functioning of which was held to be independent of small perturbations of excitation, threshold and synchrony. Thus a specific computation y = f(x) was to be embodied in a neuronal net in such a way that the various perturbations would not change f. This was the original concept of functional reliability. McCulloch’s and Pitt’s approach to this was two-fold. Their methods may be termed “scanning” and “zooming”. Given that y was to be an invariant of the distribution of excitation x, i.e., f = a, a constant, then in the scanning method, a was obtained as the average over a group G of transformations Ti of x of some functional, the various transformations of x being generated consecutively by some neuronal process. In the zooming method x was first centered (and therefore made translation invariant), and then brought to a standard from x0 by way of a convergent sequence of transformations (e.g. dilations and rotations). Evidently in the first method perturbations were minimized in the averaging process, and in the second, so long as the perturbations themselves produced only translations, dilations or rotations etc., they were eliminated.
In the second paper of this set, The Statistical Organization of Nervous Activity, published in 1948 (Paper No. 80), McCulloch and Pitts developed further the idea of functional reliability through averaging (but not scanning), with reference to more general aspects of neuronal computations, but exemplified through a calculation of the stretch reflex. The basic idea was that although the nervous system is built on all-or-nothing principles, of necessity continuous variables such as light, sound, pressure and so on, must be represented as local averages, the fidelity of which is set by the values of the space and time constants of local neuronal nets. For the stretch reflex, the quantity E(p), the expected number of all-or-none impulses arriving per unit time at a muscle, as a function of p the mean frequency of impulses emitted by that muscle’s sensory receptors, is computed as a Gaussian distribution by way of the central limit theorem. This is one of the very first statistical computations to be found in the literature of theoretical neurobiology (see also A. Rosenbleuth, N. Wiener, W. Pitts and J. Garcia-Ramos, J. Cell, and Comp. Physiol. 32, 275-317, 1948) and established E as a smooth sigmoidal function of p, rather than a discontinuous step function. Thus under the averaging operation, the mathematics of neuronal nets became analytic rather than algebraic. In this paper then, McCulloch and Pitts had reached the borders of the transition from the Boolean algebra of neuronal nets (see Paper No. 51) to an analytic theory involving integral and integro-differential equations for the probability distributions of large scale nervous activity, a theme also to be found in Norbert Wiener’s work at the same time (see for example N. Wiener, Ann. N.Y. Acad. Sci., 50, 197, 1948). In the light of later developments it is of particular interest to read their comment: “A field-theory does not now exist and may never cope with the inherent complexities. It has been shown to be unnecessary.” This comment was amplified by McCulloch in his next publication (see Paper No. 81):
“…whatever perceptions the brain is to form must be built-up by recombinations of … abstractions. Let me contrast this with any supposition that there is a conformal pattern of stress and strain in the brain, comparable to that which might be found in a system in equilibrium when the forces of the external world would determine the pattern.”
Thus rather than seeking to develop (with Pitts) such a theory McCulloch evidently began to think more about mechanisms more sophisticated than averaging, for the achievement of functional reliability.1
It was probably at the Hixon symposium that same year, 1948, that McCulloch and John von Neumann first discussed such problems. Von Neumann was apparently stimulated by their differences on Cybernetics with McCulloch, Pitts, and Wiener. The result was the 1952 Manuscript, Probabilistic Logics and the Synthesis of Reliable Organisms from Unreliable Components, later published in Automata Studies (Eds. Shannon and McCarthy, 1956). Paper No. 140, The Stability of Biological Systems, published in 1957, was McCulloch’s initial response to Von Neumann’s stimulus. In it McCulloch formulated and attacked the problem of securing functional reliability in neuronal nets despite threshold shifts, both systematic and uncorrelated. The paper is noteworthy for McCulloch’s utilization of a novel form of Venn’s diagram for the representation of the first order propositional calculus. Using such diagrams, which McCulloch termed “chiastan”, it was relatively easy to construct neuronal nets with the requisite properties, at least for functions of not more than 4 or 5 logical variables. Paper No. 144 extends the analysis a little further. The basic prin-ciples underlying such constructs are (1) to find a balance between excitation and inhibition in nets of logical depth 2, that is stable under systematic threshold shifts, and to iterate such nets into ones of logical depth 2n; and (2) to increase the logical degeneracy (or functional redundancy) by increasing the number of logical variables 8 in the function to be computed, thereby gaining some protection against random errors. Note however, that errors were not truly random, but were assumed to be segregated, occurring only for some sets of logical variables, and not for others. In the next paper, No. 160, Anastomotic Nets Combating Noise, McCulloch gave an account of the reliability of the brain stem respiratory mechanism under anesthetized conditions, in terms of the above analysis. Stability of the respiratory mechanism is obtained as a consequence of the logical stability of two-layered nets under common shift of threshold. There is also a discussion of the problem of dealing with truly random errors, produced for example by noisy axons, a form of von Neumann’s problem. This problem was dealt with by increasing the logical depth, and by the use of von Neumann’s technique of multiplexing or “bundling”, in which any function is computed, not by a single neuron, but by a group of n neurons, the connections to and from which are arranged in bundles (see No. 160, Fig. 10). The redundancy created by such an arrangement was shown by von Neumann, in the cases δ=2 and 3, to lead to increased functional reliability, provided the number of neurons in any group was at least 1,000. McCulloch, Cowan and number of neurons in any group was at least 1,000. McCulloch, Cowan and Verbeek showed that the same functional reliability could be achieved in a much less redundant net, in fact with an n of at least 20 rather than 1,000, provided that the logical degeneracy δ be increased from 2 or 3 to a value equal to n. This result depends crucially on the presumption that the reliability of neurons is independent of their logical degeneracy or complexity.
In a further piece of work Winograd and Cowan improved on this result by employing error-correcting codes in such a way that groups of n neurons computed not one, but k specified functions, thus achieving a still lower redundancy of k/n, rather than l/n (Reliable Computation in the Presence of Noise. S. Winograd and J.D. Cowan, MIT Press, 1963). This result was obtained at the cost of an increased neuronal complexity, and again required the assumption that neuronal reliability is independent of neuronal complexity.2 As McCulloch noted in Paper No. 160, the Winograd-Cowan theorem is the analog of Shannon’s famous noisy-channel coding theorem of information theory, and implies that there is a capacity for computation just as there is for communication in the presence of noise. In Paper No. 170, Reliable Systems Using Unreliable Elements, McCulloch surveys all these investigations, and ends by speculating that the notions of Cowan and Winograd relating redundancy, complexity,and degeneracy to functional reliability may find application not only in the theory of reliable neuronal nets but in theories of the reliability of protein synthesis.
Further Developments
It is of interest to consider the relationship between the above investigations, and related works. One problem not considered in detail by the McCulloch group was that of stationary rather than transient errors. This problem is of some importance in that a basic defect in both the multiplexing and error-correcting coding techniques employed, both of which rely on majority voting for the detection and correction of error, is that so far as stationary errors are concerned, since some inputs may be permanently in error, a consistently reliable minority may be outvoted by a consistently unreliable minority. Such a limitation may be overcome for the generalized voting or majority element shown in Figure 1 (see W.H. Pierce, Failure Tolerant Computer Design. Academic Press, N.Y., 1965). Such an element is a linear threshold element with variable weights. It computes the quorum function sign
all inputs taking the values +1 or = 1. If input errors are statistically independent the vote weights ai can be chose so that the output is the digit most likely to be correct, on the assumption that what is required is the reliable computation of the quorum function. If the error probability of the ith input is pi then the weights ai that give such an output are ao = log [(a priori probability of +1) / (a priori probability of -1)] and ai = log (qi/pi) where qi = 1-pi. If any input is completely random then pi = 0.5 and ai = 0, otherwise ai increases monotonically as p; approaches 0 or 1. The required vote weight settings may be obtained by comparing the inputs with the output and simply counting the number of coincidences between the values. Thus in a cycle of M operations, if Pi is the number of such coincidences and Qi the number of disagreements, then the settings a; = log (Pi/Qi) will provide the appropriate weights. Provided suitable limits are placed on the possible values of the ai it can be shown automatic weight-setting controlled by feedback from the output can serve to optimize the weights.
This result is of great interest because it provides an alternative to the use of stored error-correcting codes embodied in more complex neuron models, but of course threshold elements with variable weights are also complicated.
Another problem not considered directly by the McCulloch group was that of dealing, not with internal malfunctions and failures,
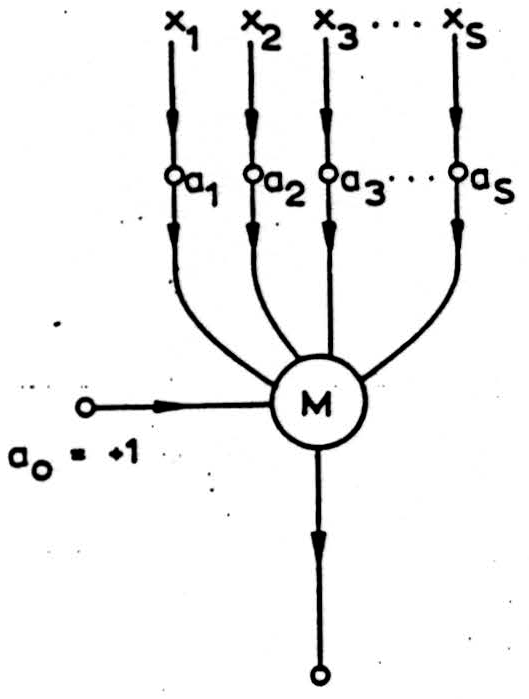
Figure 1. Generalized majority element.
but with stimulus ambiguity. This problem is particularly acute in multiplexed nets of the Winograd-Cowan type, in which the patterns of activity transmitted by bundles of connections are used to code for many functions or inputs rather than just one, but it is also seen in von Neumann’s original multiplexed nets. Thus in a bundle of n multiplexed lines, to transmit more than one bit of information requires the use of patterns other than all lines active or none active. Let the number of active lines in any such pattern be r. Then there are exactly patterns of r active lines, and so at most log2 bits can be transmitted per bundle of n lines. However the decoding problem is complex in that given a active line may belong to several patterns. Let w be the number of common lines. If r/n is substantially larger than 0.5, then w/n is likely to be at least 0.5, and the decoding problem is not simple. The Winograd-Cowan decoding algorithm can handle such problems, but this was not realized in the early 1960’s. In 1965 P.H. Greene (Bull. Math. Biophys., 27, 191-202), building on earlier work of C.N. Mooers (IRE Trans., PGIT-4, 112-118, 1954), essentially solved the problem. Independently of this, in 1969 D.C. Marr (J. Physiol., 202, 437-470) building on the work of G.S. Brindley (Proc. Roy. Soc. Lond. B, 174, 173-191 (1969)) solved the problem in a very similar fashion. Their solutions can be described as superimposed random subset coding. Let the number of active lines in a subset be k. Then there are exactly different subset
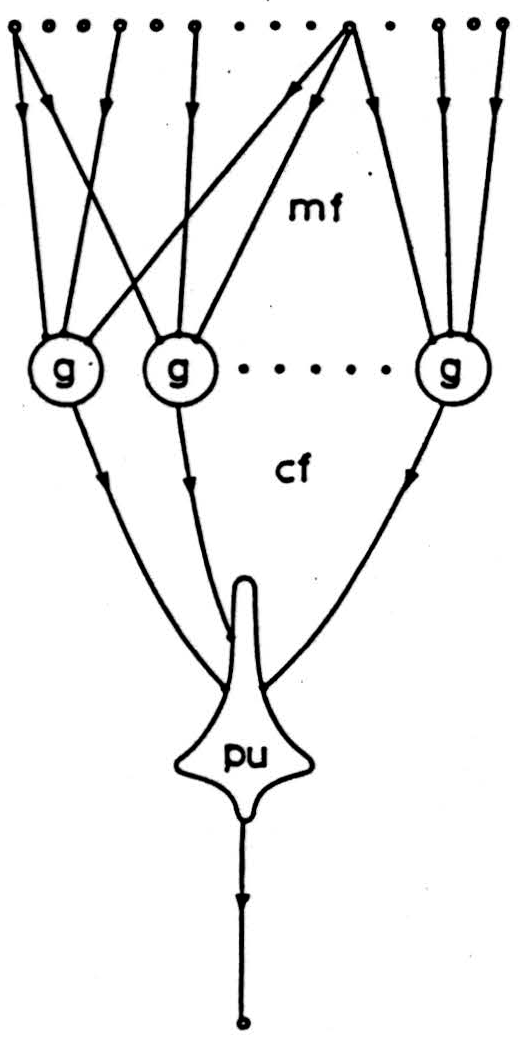
Figure 2. Detail from Marr’s model of the cerebellum.
mf = mossy fibers, cf = parallel fibers, g = granule cell, pu = Purkinje cell.
patterns in a pattern of r active lines, and exactly subset patterns in the pattern of w active lines common to two overlapping sets of r active lines. Marr noted that the fraction of subset patterns shared with an overlapping pattern tended to the ratio (w/r)k for sufficiently large w. Such a ratio decreases with increasing k. Thus the trick to unambiguous decoding is to separate a pattern into random subsets, termed codons by Marr, and to perform a threshold calculation on the number of such codons in any given pattern. Figure 2 shows the skeleton of Marr’s scheme, and for comparison, Figure 3 shows the Winograd-Cowan decoding algorithm. It will be seen that the two schemes are virtually identical, and in fact, both schemes are simply implementations of
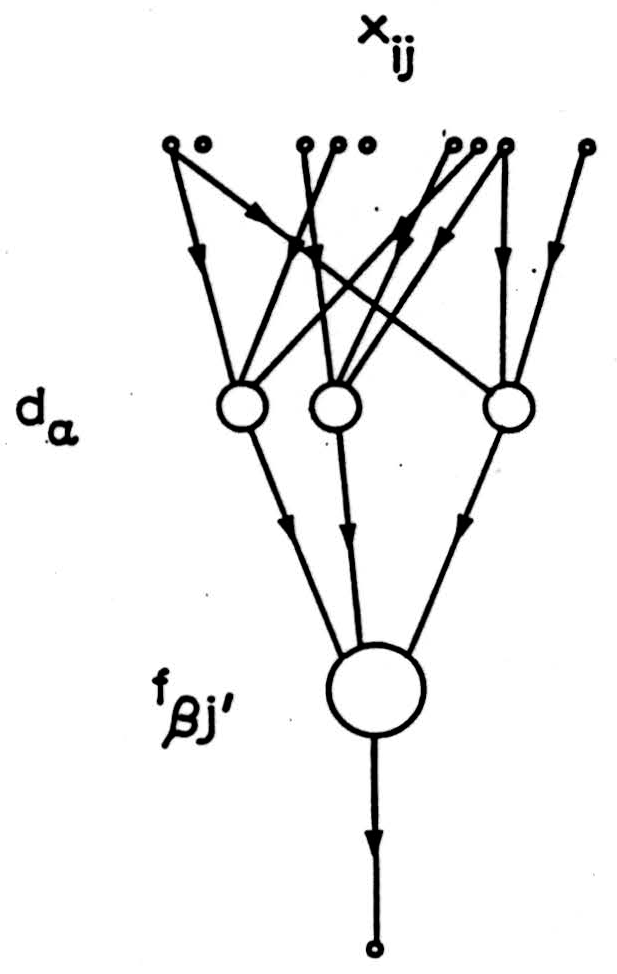
Figure 3. Winograd-Cowan decoding algorithm. da = random subset decoders fβj' = a function of da’s.
the decoding algorithms developed in the theory of error- correcting codes. However, the McCulloch group proposed that such algorithms were embodied en bloc in large neurons and their attendant circuitry, whereas Marr proposed that the differing components of the algorithm, codon detectors and codon pattern detectors, were embodied in neurons. Thus in the cerebellum, the granule cells supposedly detect codons in the mossy fiber activity pattern, and Purkinje cells detect codon patterns in the parallel fiber activity pattern. Marr also proposed that Purkinje cells learned which codon sets were to be stored somewhat analogously to Pierce’s scheme under external control but this aspect of his theory, while of great interest, is outside the scope of this discussion. A closely related investigation was also published by

Figure 4. Sabah’s model of the cerebellum as a redundant net.
mf = mossy fibers, gij = granule cells. pf = parallel fibers, puj = Purkinje cells, t = cerebellar target cells.
Sabah (Biophysical J., 11, 5, 429-445, 1971) who proposed that the cerebellum was organized to permit cerebellar target neurons to function despite noise or uncertainty, rather than ambiguity, in their Purkinje cell afferents. Thus, Sabah’s interpretation of the cerebellum was that it functioned as a “noise smearer” converting correlated fluctuations in mossy fiber activity into uncorrelated fluctuations of parallel fiber and Purkinje cell output activity. But such a scheme can again be seen in terms of a generalized decoding-encoding algorithm of the type described by Cowan and Winograd. Figures 4 and 5 make this explicit, contrasting the Sabah scheme with the full algorithm of Winograd and Cowan.
To summarize the developments since 1962, it is evident that the main point has been the realization that the modules considered by the McCulloch group are best interpreted, not as individual, highly complex neurons, but as entire sets of simpler cells, and that the real reliability problem concerns stimulus ambiguity and uncertainty, and perhaps errors of connection, rather than
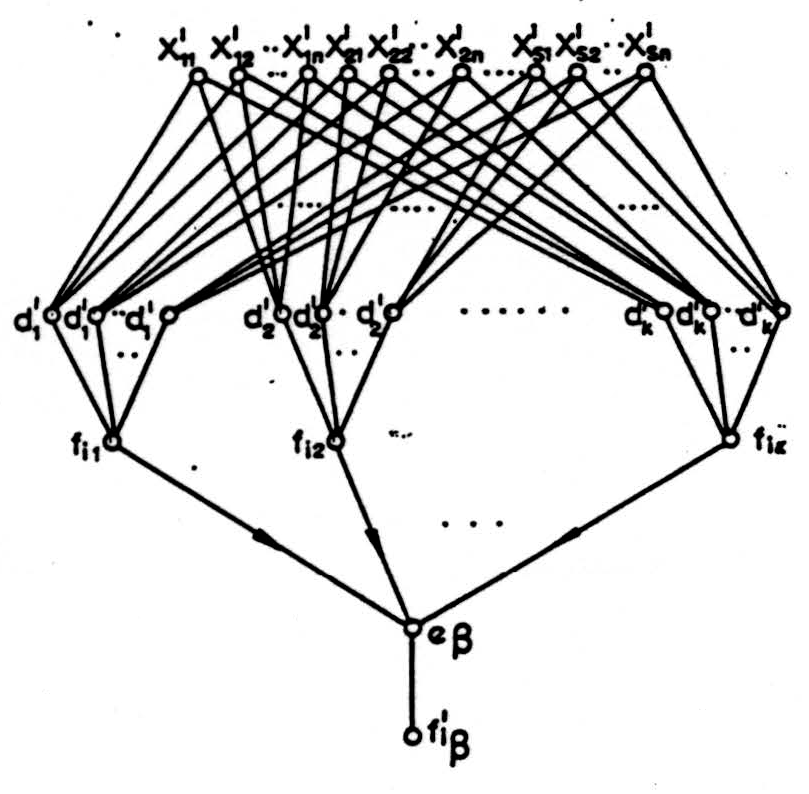
Figure 5. The full Winograd-Cowan decoding-encoding algorithm:
f’iβ = eβ [fij(d’1,…,d’1)] j = 1,…,n, β = 1,…,k.
intrinsic fluctuations in the firing of neurons. Given such reinterpretations, the work of the McCulloch group can be seen to be of a somewhat basic nature, in the theory of the functional organization of neuronal nets.
Large Scale Nervous Activity
There is one other recent development that deserves comment. This concerns the development of a true field-theory of neuronal activity, suitable for the representation of events in neuronal tissue, in a relatively continuous fashion, as opposed to the discrete representation of the McCulloch-Pitts theory. Although McCulloch (but not Pitts) asserted that such an approach was unnecessary, it has turned out to be a very useful way to think about the functioning of neuronal nets (see J.D. Cowan, Large-Scale Nervous Activity, Proc. AMS Symposium on Mathematical problems in the Life Sciences VI, AMS Publications, 1974 for references). The trick in going from a discrete to a continuous representation of events is already foreshadowed in McCulloch and Pitts’ paper on the statistical organization of nervous activity (Paper No. 80) and involves the local averaging of neuronal activity, both spatially and temporally. Thus instead of the Boolean variable fi(t) signalling the all-or-nothing firing of the ith cell at the instant t, one uses instead the continuous variable F(r, t), the proportion of cells becoming activated per unit time in a volume element dr of neuronal tissue, within the interval (t, t+dt). The resulting field-theory takes the form of nonlinear integro-differential equations of a type undoubtedly contemplated by Pitts, Wiener, and von Neumann. In such a representation the problems of reliability of signal processing become problems of dynamical stability and of non-equilibrium phase transitions, and take on a form that appears to differ from the essentially combinational problems considered by the McCulloch group. However the difference is spurious, and many of the concerns formulated and addressed by Warren McCulloch are alive and flourishing to this day, if in a somewhat different mathematical guise from that which he worked with in the period from 1943-1963.
Footnotes
For further research:
Wordcloud: Activity, Ai, Algorithm, Averaging, Cells, Codes, Codon, Complexity, Computed, Cowan, Decoding, Developments, Different, Element, Errors, Form, Functional, Group, Increased, Inputs, Limits, Lines, Logical, McCulloch, Nervous, Nets, Neumann, Neuronal, Number, Paper, Pattern, Pi, Pitts, Problem, Published, Random, Rather, Redundancy, Reliability, Result, Scheme, Subset, Theory, Threshold, Variable, Weights, Winograd, Work
Keywords: Reliability, Cowan, Perturbations, Forms, Papers, Excitation
Google Books: http://asclinks.live/u65h
Google Scholar: http://asclinks.live/9c4x
Jstor: http://asclinks.live/fh94