FACTORS LIMITING THE MAXIMUM IMPULSE TRANSMITTING ABILITY OF AN AFFERENT SYSTEM OF NERVE FIBERS12 [136]
P.D. Wall, J.Y. Lettvin, W.S. McCulloch and W.H. Pitts
Experimental Findings on Impulse Transmission from Peripheral Nerve to the Dorsal Columns
Introduction
Previous estimates of the maximum information-carrying capacity of the nervous system have been based on a maximum rate of firing, 800-1,000 impulses per second. However, frequencies of this order are almost never attained in nature. It was assumed that the nervous system had not evolved in such a way as to treat information with the highest efficiency within its physical limitations. It was concluded that no maximum principle of predictive value could be found. If that was so, information theory could not have the power as a predictive weapon in neurophysiology which the principle of entropy has in thermodynamics.
We suggest that this disappointing conclusion followed from a radical over-estimate of the real information capacity of single channels in the nervous system. The estimate was made from the properties of the central segment of an axon, a part generally considered the toughest and most rapidly reacting structure in the nervous system. In previous work, there has been no consideration of such possible partial blocks to frequent conduction of impulses as the junction between soma and axon and the branch points along the course of the axon. Without supplying the deficiency, we have no reliable estimate of the information-capacity of even the elementary components.
The three aims of the experiments were:
- To determine the maximum sustained frequency of nerve impulses which can be carried along a set of fibers which originate in the skin, muscles, and joints of the leg, proceed into the spinal cord, and stream toward the head in the dorsal columns of the spinal cord.
- To determine the limits on impulse transmission following a single impulse or short burst of impulses where all the impulses are carried by the same set of nerve fibers.
- To determine the limits following activity in a neighboring parallel set of nerve fibers.
We have examined those sensory fibers which originate in the leg, pass through the sensory or dorsal roots, enter the spinal cord, and pass up into the dorsal columns. The properties of the system have been examined in the midthoracic region where the fibers are en route toward the head, having given off many side branches. Most of the sensory fibers approaching the spinal cord, with the exception of the largest and fastest proprioceptive fibers, send a branch up into this ascending dorsal column system. A sensory fiber entering the spinal cord sends off a large number of fine branches which penetrate the depths of the cord in the zone of entry and there end at synapses. However, the main ascending branch usually continues without interruption and forms one of the fibers in the dorsal column.
On stimulating a set of sensory nerve fibers so that a single synchronized volley enters the spinal cord, two groups of impulses ascend the dorsal column.
The fastest component of the first group can be safely assumed to be made up only of nerve impulses traveling in the ascending branch of the original fiber in which the impulses were generated. These nerve impulses have not passed near to or through a synaptic region. The later arriving components of the first group may be slowly conducted impulses of a similar type or may be impulses which have been relayed into the dorsal column by way of spinal cord internuncial cells. Since we are concerned only with the process of the delivery of impulses along the simplest possible channel, that is to say, a continuous axon approaching but not reaching a cell, we shall report only the behavior of the earliest components of the first group.
The second group is made up of impulses whose significance is controversial. They originate in the region of the fine terminals of the sensory fibers either because of “echoing" off the end of an active fiber or because of “cross talk” from a neighboring active fiber. This phenomenon, the dorsal root reflex, is greatly exaggerated by cooling and other abnormal conditions but can be detected even under the best experimental conditions. Precautions were taken to prevent confusion of this second group with the direct conducted impulses whose behavior we wished to study.
Experimental Conditions
Decerebrate, spinal, or barbiturate anesthetized cats were used. Motor movement was controlled either by section of the ventral roots or by curare. The required parts of the spinal cord were exposed by limited laminectomies. Temperature of the whole animal was controlled by a thermistor embedded under the scapula regulating heat lamps below the animal. Evaporation from exposed surfaces of the nervous system was prevented by covering with mineral oil saturated with 5 percent CO2 - 95 percent O2 in order to maintain the normal functioning of sectioned nerve trunks.
A number of different recording methods was used in order to take advantage of the special properties of each of them. The problem of recording the volleys in the dorsal columns needed special attention. The simplest recording method was to place electrodes on the surface of the intact dorsal columns. The recorded volley was small owing to the triphasic nature of the individual impulses in a volume conductor and was contaminated by potentials originating outside the dorsal column. An improvement in the height of the recorded volley could be obtained by blocking the dorsal columns by local application of procaine. This method of blocking has the advantage that the nerve membrane is not depolarized, so that the special complications of firing a high-frequency burst of impulses into a depolarized region do not occur.
All of the phenomena to be reported could be seen in this type of recording so that it is certain that the results obtained from more radical recording methods were not due to the damage of the dorsal columns. A great increase in the height of the recorded volley was obtained by sectioning the dorsal column and recording the collision of the impulses with the cut end of the conducting nerve fibers. A further increase and isolation from other potentials were obtained by dissecting and lifting up a length of the dorsal column so that the cut end was isolated from surrounding tissue. In order to avoid confusion between the total number of nerve impulses and their synchronization, we have recorded not the height of the volley but the area.
Results
1. Maximum sustained frequency of nerve impulses.
Nerve impulses were examined at three points of their progress along continuous axons, to wit, the sciatic nerve, dorsal root, and dorsal columns. Stimulating and recording electrodes are placed on an isolated and sectioned part of the sciatic nerve, dorsal root, and dorsal column. Supramaximal stimuli are delivered from 10 to 500 per second.
Figure 1 shows an example of the change of the height of the volleys at different frequencies of stimulation. In this experiment, the cat was anesthetized with barbiturate, and the dorsal columns were cut and isolated for stimulation and recording. The right hand curves represent the ability of the dorsal root axons or the sciatic nerve axons to respond to a sustained frequency of stimulation. The time is the interval between successive stimuli and the height is the size of the volley of nerve impulses at that frequency expressed as a percentage of the height of the volley at extremely low frequencies (1 stimulus every 2 seconds). The right hand curve in the sciatic nerve picture also represents the ability of impulses to pass backwards in the unphysiological direction from the dorsal columns through the root entrance zone and down the sensory fibers in the sciatic nerve. The left-hand curves in the two pictures show the result if the sciatic nerve or a dorsal root (the
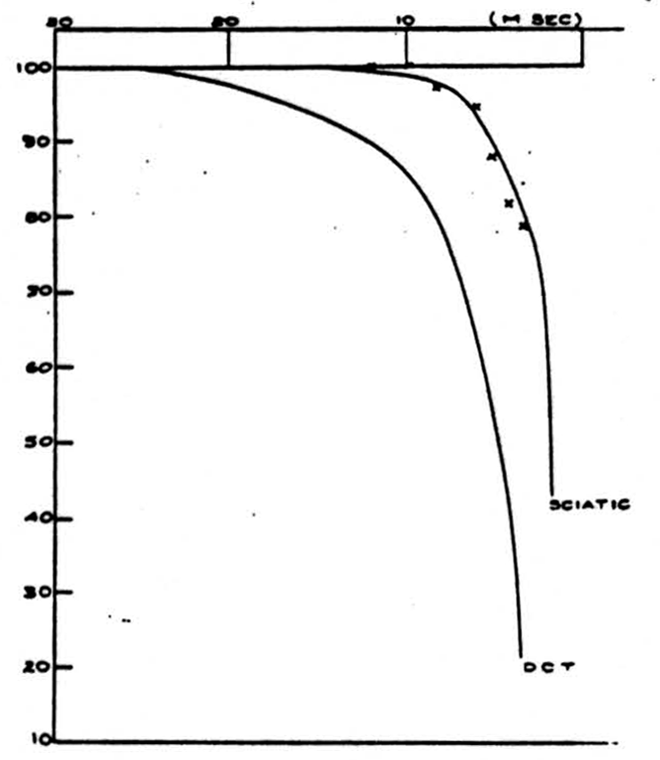
Figure 1(a). SCIATIC TETANUS

Figure 1b. ROOT TETANUS
seventh lumbar) are stimulated and the impulses are recorded in the dorsal column after passing the root entrance zone. It should be stressed again that this pathway is made up of a bundle of single continuous axons.
It will be seen that the ability of the dorsal root or sciatic nerve to conduct impulses at high frequency is superior to the ability of the sciatic-nerve-or-dorsal-root-to-dorsal-column channel. However, it will be noted that if the impulses are generated in the dorsal column and pass backwards into the dorsal root and sciatic nerve, the frequency limitation is the same as if the impulses were generated and recorded in a peripheral axon.
The reason for the decrease in the height of the recorded spike at high-frequency stimulation is threefold. First, at very high frequencies the height of the individual action potential decreases (relative refractory period). Second, during this time the threshold increases so that some fibers may not fire off. Since the stimulus was supramaximal, this second effect did not appear. Lastly, and this is the main effect in which we are interested, fibers reach a frequency at which they can no longer respond to every stimulus and proceed to respond to every second stimulus. As the frequency reaches above 100-200 per second this tendency becomes organized so that a regular alternation in heights begins to occur. This alternation explains why the observed heights have not been recorded for the higher frequencies even though the absolute refractory period has not been reached.
2. The effect of a burst of activity of short duration in the tested channel on the subsequent passage of impulses.
Far more striking than the limitation on a steady rate of transmission is the effect of a single impulse in each of a parallel group of entering nerve fibers on the subsequent ability of those nerve fibers to carry a second impulse. In unanesthetized spinal preparations a partial block of the second volley of impulses lasts for 30-40 milliseconds after the first. In animals under barbiturate anesthesia the effect of the single volley is greatly exaggerated and prolonged to over 100 milliseconds. The effect is not constant but is markedly present in well over half of the animals used. Strychnine and asphyxia abolish the effect. Slides will be shown of the various aspects of this phenomenon. Short bursts of high-frequency impulses exaggerate in intensity but do not prolong in time the blocking of subsequent nerve impulses.
3. The effect of preceding activity of short duration on the ability of a neighboring channel to conduct impulses.
A similar block of impulses, in a group of nerve fibers which have not been active, follows the passage of a single impulse in each fiber in a neighboring channel. The intensity of this block is not quite as great as the block following the activation of the same channel. The time course of the blocks is, however, identical. It may well be that the phenomena described in this and the preceding section are the same. The importance, however, is that it establishes a serious interaction between neighboring channels which might not have been predicted from a study of nerve impulses following each other in the same channel.
4. The contrast of ortho- and antidromicalty conducted impulses.
The ability of the nerve fibers to sustain a steady frequency was shown in the first section to depend on the direction of travel of the impulses. It was similarly shown in section 2 that when one volley of nerve impulses follows another from the dorsal roots into dorsal columns, blocking occurs if the interval is short. In contrast to this, if the impulses are generated in the dorsal columns and travel antidromically in the opposite direction to the physiological one, no signs of prolonged block can be detected. A most striking example of this will be shown where a single microelectrode is placed in the dorsal columns close to the root entrance zone. On stimulation, impulses flow away from this point of stimulation in the two directions. Two stimuli are given a various intervals. The second volley proceeding up the cord is shown partially blocked for 100 milliseconds after the generation of the first. The second volley proceeding backwards down the same fibers and out of the dorsal roots shows no prolonged blocking but a slight facilitation or the lowering of the threshold of the dorsal column fibers by the prolonged negative after-potential which these fibers exhibit.
It will be seen that we have demonstrated two phenomena: (a) Impulses tend to be blocked during their passage along the continuous axon in the region where side branches emerge, (b) This block occurs only if the impulses are traveling in the normal physiological direction from their peripheral origin into the central nervous system. If impulses are artificially generated in the central parts of the axon, the impulses emerge traveling toward the periphery without any special limits on their progress. At present, we can only speculate on the reason for this valve action.
Two groups of theories can be produced. First, special properties of the axon itself may be the cause of the one-way block. The axons we have been considering are myelinated axons. Each fiber is covered with an insulating sheath of myelin which is broken at regular intervals, the nodes of Ranvier. As the axon approaches the cord and just before giving off its first two main branches, the myelin disappears along with a surrounding layer of cells, the Schwann cells. The fiber is bare, without a myelin covering, for some distance on either side of every branch point. The frequency of branching is highest at the point of entry into the spinal cord. At each division point there is a slight decrease in diameter of the subsequent fibers. Either the gradual tapering of the fibers or the presence of the unmyelinated segments of nerve in higher frequency and length close to the entry point of the fibers might constitute the one-way hazard to conduction which we have demonstrated.
The second group of theories depends on activity outside the conducting axons. The side branches of the main axon penetrate into the depths of the spinal cord. Activity is generated in the endings of these branches and in the nerve cells which they contact. These potentials may spread back and affect the impulse transmission along the parent axon. Since the side branches are most concentrated at the point of entry of the parent axon into the spinal cord, there is an asymmetry, so that the entering impulse encounters a greater potential gradient than the leaving impulse. Experiments are in progress to test some of these theories.
5. The ability of a physiological stimulus to block a synchronized volley of nerve impulses in a neighboring tract.
The general significance of this interaction blocking of nerve impulses in neighboring tracts has been greatly increased by the discovery that a pinch stimulus to the skin of the leg is quite as efficient, if not more so, as a single synchronized electrically produced volley in producing a period of block after the passage of the volley.
Experimental Conclusions
We have demonstrated three physiological effects that will reduce the information-carrying capacity of a simple afferent nerve fibre system below the level expected from data derived from the axons in their uncomplicated peripheral course.
- The maximum sustained frequency of transmission of nerve impulses through a region where side branches of the main axon are given off is considerably less than was previously believed.
- The presence of a short preceding burst of activity in a set of fibers limits the subsequent ability of the fibers to conduct.
- The presence of a short preceding burst of activity in a neighboring set of fibres limits the ability of previously inactive fibers to conduct.
The second section of this paper takes one of these experimental findings, the reduction of the maximum rate of sustained firing, and proceeds to determine how much such a reduction will affect the maximum information transmission capacity. It is clear that this physical limitation of the transmission system brings the maximum attainable frequency of impulses closer to the maximum frequency of nerve impulses actually recorded from those types of stimuli which occur in nature. The analysis which follows seeks only the maximum and disregards a number of additional phenomena -- all of which would tend to reduce the capacity of the channel below the maximum to be calculated. At least three additional limiting factors have been disregarded. Nerve fibers have a resting rate of discharge under conditions of minimal stimulation which will naturally set an upper limit for the usable interval between nerve impulses. We have demonstrated an interaction between neighboring channels whereas in the analysis we consider only the behavior of an artificially isolated channel. Third, nerve impulses pass from one axon to the next cell by way of a terminal arborization in which the parent fiber breaks up into a large number of fine branches; it is quite certain that such branches further limit the maximum rate of impulse transmission.
Since it has not yet been possible, in practice, to measure the extent of these other hazards, we are limited here to an analysis of the quantitative effect of the phenomena described in section 1. However, since our purpose is to demonstrate that previous analyses of maximum information capacity have been based on far too high an estimate of maximum frequency, we shall be able to demonstrate a much lower maximum. Intuitively, we can say that there are a number of additional hazards to transmission which we have not considered which will further limit the information capacity. A final consideration of the total effect of these hazards may still show that the nervous system is handling information at the fastest rate allowed by the limitations of the components of the nervous system, although we do not necessarily subscribe to such a hypothesis.
The Information Capacity of the Channel from Peripheral Nerve to the Dorsal Columns
The assumptions of MacKay and McCulloch about the mode of transmitting information along simple axons appear to be the most general ones compatible with physiology, so that we shall adopt them as a basis for calculation. They run as follows:
- A message along an axon consists of a sequence of impulses separated by intervals differing in duration; the possible durations of these intervals constitute the symbols conveying the information.
- The durations of intervals can be discriminated down to a certain small interval of time Δt but no further, so that when Δt is taken as the unit of time the intervals are effectively integral multiples of it. This assumption is a simplification, but it is unlikely to be dangerous. We shall take Δt as 0.05 msec, like MacKay and McCulloch.
- No interval is shorter than R. Note that here the meaning of the term is somewhat different from the usual meaning. Since we are considering a statistically homogeneous steady state, R will have to be the minimum interval at which impulses can be indefinitely conveyed - or, at least, one that can occur with appreciable frequency.
- Intervals at different times can be made statistically independent. This gives a higher information capacity, and we are seeking an upper bound for this quantity.
Let the probability of an interval’s having duration n be ϕn. We shall take ϕn = 0 for n < R, the refractory period; then
- The series
is assumed to converge; it represents the mean length of interval, the reciprocal of the mean frequency.
The mean rate of conveying information in time will then be, in exponential units,
If we maximize H with respect to all the ϕn, subject to the condition of Eq. 1 we find straightforwardly
where H is the positive solution of the equation.
(Note: This corrects the mistake in the calculations by Mackay and McCulloch. The mistake does not affect their conclusions: it even requires us to raise their numerical estimates somewhat. Thus if R = 20, H = 3.3 binary bits per millisecond, instead of their value of 2.9 bits, and a = 1.36 msec, giving a mean frequency of 735 impulses per second instead of 620.)
There is no maximum interval, the longer ones becoming exponentially infrequent.
Let us suppose that an axon A carrying a message fulfilling assumptions I-V enters a zone Z, whence another axon B (say a branch of A) emerges. We consider Z to be primarily the region between the entrance of the dorsal roots into the spinal cord and the thoracic dorsal columns, or some fraction of it. We shall suppose that the passage of a message through Z affects it in the following way:
VI. A certain proportion a of the entering impulses is abolished, and this is done randomly and independently for different impulses. The remaining impulses are transmitted out B unchanged except perhaps with a uniform time delay. a is a function only of the mean frequency of the entering impulses.
This rule is something of a simplification of the experimental facts about the inhibition described in section 1. It is equivalent to supposing that the average amount of inhibition produced is independent of the grouping of the afferent impulses, as long as the total number per unit times is the same; it is evidently not strictly true, but perhaps enough so for the crude considerations that follow. The same holds for the independence of the probabilities of inhibiting successive impulses. To take the inhibition given by the reduction in the average size of the output as a function of the frequency of the input has experimental advantages as well as mathematical ones. The function is convenient to measure, and it refers to a state of continual stimulation more likely to be natural than one of rest punctuated by occasional pairs of test stimuli.
If we assume that the relative heights of the monophasic dorsal column spikes represent the relative numbers of impulses transmitted, the data of Fig. 1 give us a directly as a function of a, the interval between afferent volleys. It is convenient to have a simple expression representing the relation approximately: we find that a single negative exponential represents it within about 5 percent. Thus
where λ and R’ are constants and where for stimulation of the dorsal root and recording from dorsal columns
R^'^ = 0.521 (msec)
λ = 0.165 (1/msec)
and for stimulation of the sciatic nerve
R^'^ = 2.39 (msec)
λ = 0.287 (1/msec).
Our computations require using Δt = 0.05 msec as the unit of time, in which units the latter values become R’ = 47.8, and λ = 0.0143.
Let ϕn be the frequency of intervals of length n in the entering message on A. If an impulse is abolished, the intervals it separates coalesce into a longer one: the frequency ψn of intervals of length n in the message emerging along B will therefore be different from ϕn. We may find it as follows. Let
be the power series with ϕn as nth coefficient; from Eq. 1 ϕ(x) will be analytic in and on the unit circle. Let n1, n2…ns, be successive intervals in the incoming message. Then
where C lies inside the unit circle, as is well-known,
and so on.
Consider an interval N in B emerging from Z, and suppose that it begins with the same impulse as begins n1 in the input. The probability ψn that the emerging interval shall have length N is the sum of the contributions from the following series of mutually exclusive cases:
- The next afferent spike is not abolished, and n1 = N.
- The next spike is abolished, the following one is not, and n1 + n2 = N, and so on, including a term for every series of intervals which can coalesce to produce one of length N. Hence
so that
the calculation is valid, since a<1 and |ϕ|<A<1 on C. Clearly,
and
whence
ψn⩾0. (8)
The mean interval b of the output is
as we should expect: loss of a proportion a of the impulses reduces the mean frequency to 1 - a times its former value.
We seek to calculate the information capacity of the sequence of channels A, Z, B. If X and Y are messages in A and B respectively, the information capacity is defined as
C = H(X) + H(Y) - H(X, Y)
where H(X) and H(Y) are the rates of conveying information along A and B, H(X, Y) is the joint information conveyed by the pair of messages on A and B together, and the statistics of the messages on A and B are chosen so as to make C a maximum. We consider only probability distributions rendering successive intervals independent, so that
with the ψn determined from the ϕn by Eq. 7, the ϕn to be found. [It follows from V that H(X) and H(Y) exist and are finite: if Σn ϕn converges, ϕn≥0, nϕn< , ϕn< for Y sufficiently large). Hence Σϕn log ϕ converges; and similarly, for ψn from Eq. 10)]. H(X, Y) can be found by remarking that the knowledge of the message and noise together consists of knowing what lengths the input intervals have, and, for each interval, the answer to the question of whether or not the impulse terminating the interval fails. The latter information is
per unit time, since a is the probability of failure, and there are b-1 such impulses per second. The former is simply H(X). We should expect the informations to be additive, since the signal and noise are statistically independent, and so find
bH(X, Y) = -a log a - (1-a) log (1-a) -Σϕn log ϕn.
Consequently
C is now to be made a maximum among all sets ϕn satisfying the conditions
- ψn ⩾0, ψn = 0 if n < R;
- Σψn = 1;
- The ψn are derivable from a series of numbers ϕn such that
ϕn ⩾0, Σϕn = 1, ϕn = 0, n < R, by the relation
Condition B implies that
ϕ(1)=Σϕn = 1,
and ϕn will have the refractory period R ψn if does, so that only the positivity of the ϕn is to be secured. But this is not a consequence of conditions A and B; in fact, since
there is an infinite series of inequalities to be satisfied by the ψn:
ψn ⩾ 0, n<2R
and so on, for greater values of n.
In addition, Eq. 9, as well as these inequalities which constitute a complete set of conditions, yields
b(1-a) ⩾ R. (15)
It does not seem easy to find the maximum of C in the class Y of sequences fulfilling A, B, and the inequalities of Eq. 14. We shall therefore maximize it in the wider class of sequences fulfilling A, B, and Eq. 15, but not necessarily Eq. 14, in order to find an upper bound for the information capacity; and then maximize it in a smaller class contained in Y, in order to reach a lower bound for it.
It is convenient to maximize C first, subject to the constraints £ψn=l and £nψn, taking b as a fixed parameter. One obtains
If C is now made a maximum as a function of b, without further restrictions, we find
where a'= (da)/(da), determining b = a(1-a) and C implicitly.
To set a lower bound to the information capacity, we observe that according to Eq. 13, .
so that for this range of n the positivity of ϕn follows from that of ψn. If the ϕn be compelled to vanish beyond n = 2R - 1, condition C will certainly be satisfied, and ϕ(x) becomes a polynomial of the (2R - 1)st degree:
whence
The first R ψn may therefore be determined arbitrarily, subject to the conditions
ψn ⩾ C, n < 2R,
and
and the later ψn calculated from Eq. 18; the resulting sequence satisfies all the conditions (A, B, C), and has a mean given by
We find the lower bound for C by maximizing the quantity
with respect to ψR, ψR+1, …, ψ2R-1; the resulting ψn = ψn* determine a θ1 which does not exceed
in which the for n⩾2R are obtained from the earlier ones by Eq. 18; θ2 in turn does not exceed
where ψ̄R, ψ̄R+1, … ψ̄R~R-1~ are those which make θ3 itself a maximum when the later ψ̄n are inserted as functions of ψ̄R, … ψ̄2R-1. θ3 is the true maximum information capacity in the class of probability distributions of inputs containing no interval greater than 2R -1.
θ1 is the only one of these quantities that is at all convenient to compute; this is done tediously, and leads to the expressions
in which p is a parameter, and a’ = (da)/(da). Here, a = b(1-a).
Conclusions
(Numerical computations of the estimates given above for selected experimental data will be presented at the conference, and the significance considered.)
Our interest, in the present case, is less in the actual values of the information capacity than in the mean frequency it determines — as in thermodynamics. Unfortunately, bounds for the information capacity do not automatically lead to bounds for the mean frequency, so that an exact solution of the problem would be very welcome. It will be seen, however, that the tendency of the inequalities (Eq. 14) is to increase the value of the mean interval, and it is likely that the upper bound for C furnishes a lower bound for a, and an upper one for the mean frequency. If this is true, we have succeeded in reducing the mean frequency which gives most efficient transmission of information to one of the normal range, and therefore obviating the difficulty, mentioned in the introduction, in supposing the nervous system organized for the most efficient transmission of information possible within its general purposes and physical limitations.
Footnotes
For further research:
Wordcloud: Ability, Activity, Along, Axon, Block, Bound, Branches, Capacity, Channel, Columns, Conditions, Conduct, Cord, Dorsal, Effect, Fibers, Follows, Frac, Frequency, Generated, Group, Height, Impulses, Information, Infty, Interval, Limits, Log, Maximum, Message, Neighboring, Nerve, Ph, Phi, Psi, Recorded, Root, Sciatic, Section, Single, Spinal, Stimulation, Sum, System, Transmission, Unit, Volley
Keywords: System, Axon, Information, Work, Blocks, Order, Impulses, Theory, Information-Capacity, Conclusion
Google Books: http://asclinks.live/fkyb
Google Scholar: http://asclinks.live/45xl
Jstor: http://asclinks.live/dj3d