LIMITS ON NERVE IMPULSE TRANSMISSION1 [130]
P.D. Wall, J.Y. Lettvin, W.H. Pitts and W.S. McCulloch
##
During the last ten years it has become increasingly apparent that we ought to think of the circuit action of the nervous system in the same terms that we use daily for complicated servo systems and computing machines. Their business is the handling of information transmitted by signals. The nature of the signals and their combination is best understood by knowing the properties of the components and the wiring diagram.
In the nervous system the components are called neurons. Each has a body and a long, thin taproot whose branches end on other neurons. The anatomy of their connections gives us the wiring diagram (Fig. 1) of the nervous system.
Since we are considering here the information capacity of the input to the nervous system from receptors in skin, joint, and muscle, we need look only at the neurons that connect the receptors to separate places in the spinal cord and brain stem. One end of the neuron is in the receptor shown on the right of Fig. 1. The other end enters the spinal cord by way of the dorsal root and divides promptly into a short descending and a long ascending branch both of which send off twigs to end locally on nerve cells near its point of entrance. The long ascending branches form the so-called dorsal columns of the spinal cord. Typical sensory nerve is a cable of, say, a thousand of these axons. A typical dorsal root is a similar cable. The dorsal column, that is, their ascending limbs, grows thicker toward the head as more ascending branches are added by each dorsal root. Think of this dorsal column, too, as a cable. It is our intent to estimate an upper bound upon the information capacity of the dorsal column.
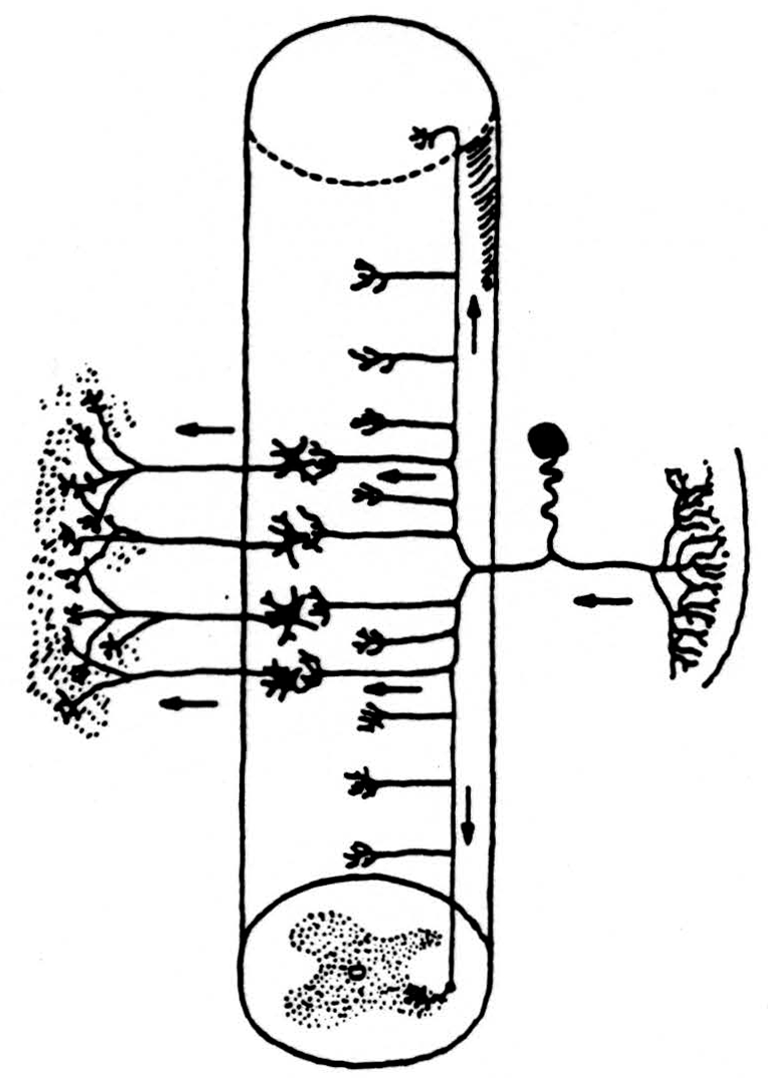
Figure 1
But to understand the experiment we must have a clear picture of the nature of the signals themselves, that is, of nervous impulses. Think of the axons in any cable as a conducting core of relatively high resistance surrounded by a thin dielectric having a capacity of pf/cm2 shunted by a nonlinear resistance, and charged 0. 07 volt positive on the outside. So long as the voltage through it is above, let us say, 0.02 volt, the resistance is enormous. Below that value the resistance is negligible — i.e., nearly a dead short.
Now, if at any point the voltage is locally reduced, current flows into the axons’ core, discharging the adjacent portion of the surrounding dielectric, which, in turn, becomes a short, thus generating an impulse that travels, like a smoke ring of current, along the axon. The axon then seals off the resistance and restores the voltage. The whole impulse requires at any one point about one millisecond and is propagated with a velocity determined by the distributed resistance and capacity, let us say, 150 meters per second for the fattest axons and less than one meter per second for the thinnest branches. For unbranched cylinders the factor of safety for conduction is about 10. So we can be fairly sure that an impulse started at the periphery will reach the spinal cord, provided it does not come too soon after a previous impulse. But at the point of primary bifurcation in the cord and in the region where these branches give off most of their twigs, the geometry requires that a relatively large area be discharged rapidly through an increased internal resistance and, by this mismatching, the factor of safety is much reduced.
Today, it is possible to record from these single axons by micropipette electrodes, about one third of a micron in diameter, and thus to detect whether or not an impulse does get through this region. But this would not give us the statistical information we require, namely, what fraction of the axons’ impulses do pass the hazardous region. Since the transients can be shown to add linearly in a nerve bundle, this fraction is measured approximately by the total voltage of the first spike to appear in the dorsal column when the whole of a dorsal root is excited.
Here is one experiment. The diagram on the right of Fig. 2 indicates at the bottom the electrodes through which we evoked a maximal synchronous volley of one dorsal root. The spike in the voltage in the dorsal columns was recorded between the side and cut end of the dorsal columns, as indicated. These records are at the left with the time in milliseconds under them. The lower record shows the spikes produced in the dorsal column by two volleys of the dorsal root separated by 40 milliseconds. The initial spike of the second response is much reduced and the subsequent hash of secondary discharges has disappeared.
The upper composite record was made by opening an electronic window that will admit only the initial spike of the volley without any hash. The conditioning stimulus was given every two seconds at a fixed time and place on the screen while the test stimulus was slowly stepped later and later in each 2 seconds. To produce this composite record, the camera was open throughout this series of experiments. At the left, the record shows the size of the unaffected response to the test stimulus. Then later, it discloses the time course of its reduction and slow recovery — out to 100 milliseconds. So much for the effect of one volley upon the ability of the same axons to transmit a second volley through the region of bifurcation.
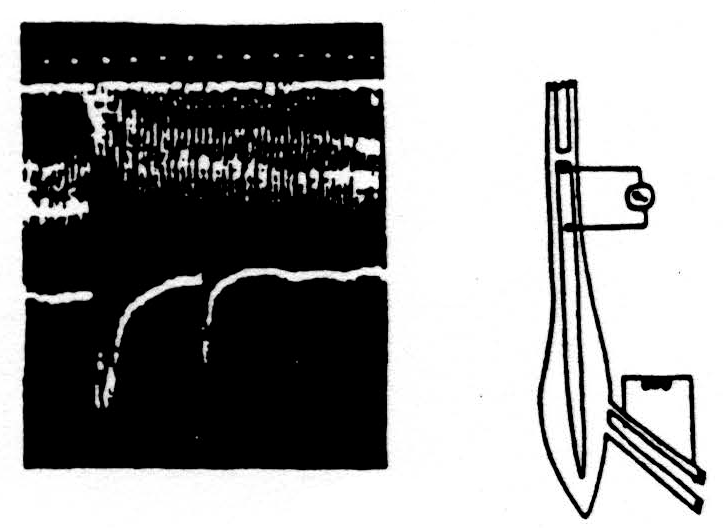
Figure 2
Here is a second experiment. (See Fig. 3.) The diagram and records are like the previous ones, except that, this time, the conditioning volley was applied through one dorsal root and the test volley through an adjacent one. The results were very similar,
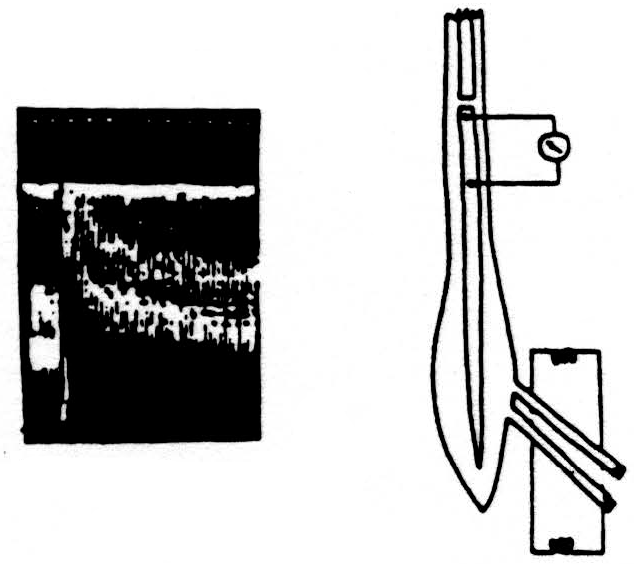
Figure 3
although in this case the axons carrying the conditioning volley and those carrying the test volley were not the same, but merely adjacent to one another in the spinal cord.
We needed both of these results, because when we consider repetitious excitation of a simple nerve at some frequency it is of importance that it does not make any great difference which of its axons happened to conduct, but only their number.
Next let us compare these experiments in which the brain has been previously destroyed, so that no anesthesia was necessary, with similar experiments under dial narcosis, which slows down the rate of repolarization. You can see from Fig. 4 that Dial prolongs as well as augments the loss of impulses. Let us add to this that although these experiments were done with a conditioning maximum volley — this is not necessary. All one has to do is to pinch a paw and the same decrement of conduction ensues, but
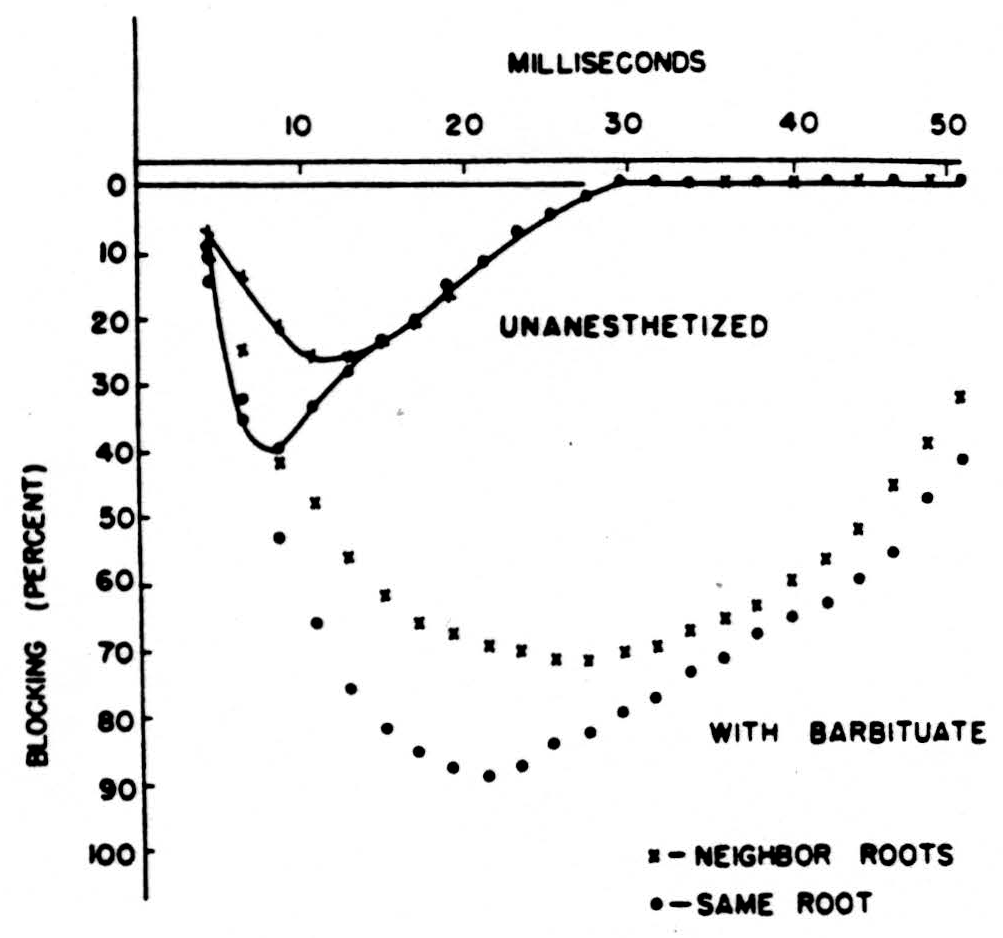
Figure 4
the pictures are not so pretty. Finally you should know that strychnine, which keeps up the polarization of the axonal branches to their maximal values, diminishes this block. All impulses get through and the result is a convulsion. Hence the block at the primary bifurcation is a normal and a useful way of gating signals by signals.
But to say that the blocking of these input channels is useful in keeping the glut of information within normal limits does not imply that it produces no loss in channel capacity. It does produce a great loss. This was proved by the experiments we have described, but they do not yield the best sort of data from which to compute the upper bound on that channel capacity. For this we want to know the decrement under the steady-state condition of repetitious firing.
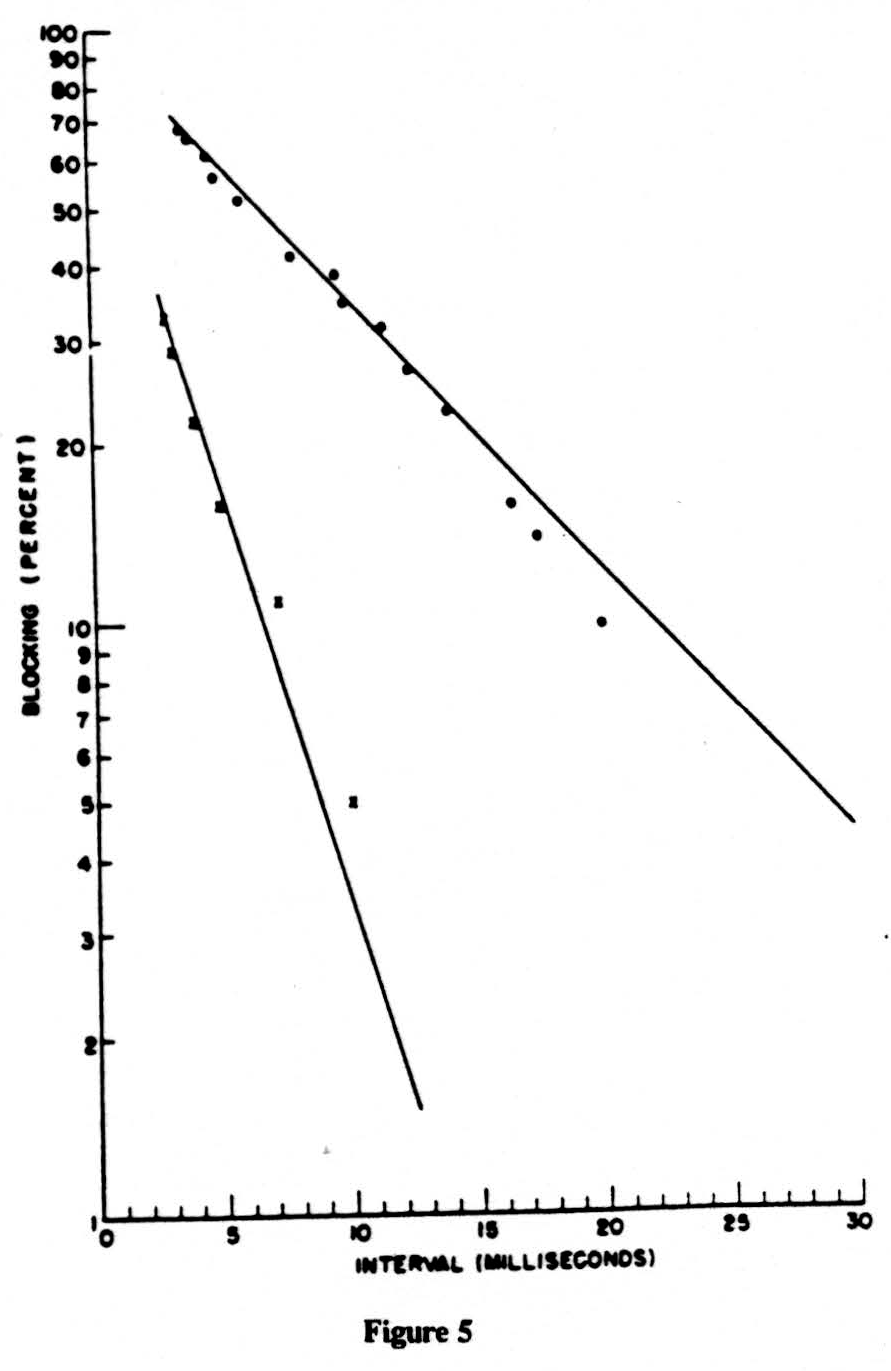
In Fig. 5 we have plotted on semilogarithmic paper the percentage of impulses lost (called the percentage of inhibition) vertically against the reciprocal of the frequency horizontally. The results are two straight lines. The one at the left is obtained on the nerve. The one at the right is for impulses coming from the dorsal root through the bifurcation up the dorsal column, that is, in the normal direction. Please remember that in this direction we must fire a region of long time constant from one of short time constant. In the reverse direction, backward from the column to the root, there should be no block, and there is none. We have plotted the points for this antidromic conduction by small x’s which, as you see, fall on the line for the nerve. If you compare the two straight lines for, say, 30 per cent decrement, you will note that this occurs at 3 milliseconds for nerve and at 12 milliseconds for the normal input to the dorsal column, i.e., at frequencies of 333 cps and 83 cps, respectively. Both lines point toward 100 per cent failure at a little under one millisecond. So much for the experimental data. It points to far lower frequencies, or lower duty cycle, in the input than previous work that had been restricted to peripheral nerves indicated.
Next we come to general notions as to how information is coded in the central nervous system. The coding problem can be divided into questions of which neurons are fired and when they fire. The first depends upon the anatomy of the nervous net, but it is most easily studied by sending signals through the system. Thus it has been shown that on each of the great areas of banks of relays in the forebrain, midbrain, and hindbrain the connections are such that they map the surface of the body and of receptors
 like the eye and the ear, thus preserving the topology of the input. This depends upon mapping neighborhood into neighborhood by the use of parallel channels. This arrangement preserves the topological properties of the sensed world despite perturbations of thresholds, scattered loss of channels, and even perturbations of the exact connections, so long as they still go to the proper neighborhood. Thus the redundancy of parallel channels insures the proper location and as it were, the proper shapes, of objects for us. The same sort of relation holds for the output. Neighboring points in these central structures are connected to neighboring points in muscles with the same obvious advantages of redundancy.
like the eye and the ear, thus preserving the topology of the input. This depends upon mapping neighborhood into neighborhood by the use of parallel channels. This arrangement preserves the topological properties of the sensed world despite perturbations of thresholds, scattered loss of channels, and even perturbations of the exact connections, so long as they still go to the proper neighborhood. Thus the redundancy of parallel channels insures the proper location and as it were, the proper shapes, of objects for us. The same sort of relation holds for the output. Neighboring points in these central structures are connected to neighboring points in muscles with the same obvious advantages of redundancy.
Time-wise the story is not so clear. When Pitts and McCulloch first proposed their logical calculus for the behavior of relay nets there was little evidence to suggest anything but simple binary coding of a system that might have been clocked in steps equal to the striking time of the relays, i.e., the duration of pulse and absolutely refractory period — about one millisecond. Thereafter it became increasingly clear that many receptors coded the logarithm of the intensity of stimulation or of its first derivative into frequency. MacKay and McCulloch, therefore studied the limits placed upon the use of pulse-interval modulation by the precision of time of firing and by the least interval detectable by a neuron. Both of these times are far shorter than one millisecond, say one-twentieth of it. In estimating the upper bound on the information capacity they made the mistake of assuming all intervals as equi-probable. This mistake was detected by Andrew, but, as Pitts has shown, it does not affect the numerical answer too greatly for such a crude estimate. Pulse-interval modulation enjoys a vast superiority over simple binary coding, passing far more information at given mean frequencies or the same amount of information at far lower duty cycles. In fact, the advantage remains with it until 100 serial relayings perturb the timing by a whole millisecond. What makes this theory difficult to accept is that the mean frequencies for maximum information flow are far higher than those typically encountered in the central nervous system, say 735, instead of less than 100.
Such a discrepancy between prediction and observation naturally persuades us to throw away the theory. In fact, many of us were ready to think all information theory useless as a guide to research in the physiology of the nervous system. It now appears that such a conclusion does not necessarily follow. The previous estimates were based on well-known properties of peripheral nerves, not on the properties of conduction through the inevitable regions where branches occur and impulses are gated by impulses. We have therefore calculated a new upper bound and its corresponding mean frequency on more realistic assumptions. These calculations are given at length in the Transactions of the London Symposium on Information Theory of 1955. They depend simply on the consideration of a system of parallel channels each of which has a dead time some twenty times the discriminable interval and an effective dead time that increases with the mean frequency, as observed. An upper bound on information capacity like this cannot define the mean frequency for optimum use; it can only put an upper limit upon it. The computed information capacity is 0.54 binary bits per millisecond and the corresponding mean frequency is 138 impulses per second. This is certainly an over-estimation of information capacity. Our upper bound is only an upper bound and not necessarily too close a bound. Consequently, the optimum mean frequency must be somewhat below 138 per second, which is about 1/5 that of MacKay and McCulloch. It certainly exceeds what we actually record. But there is nothing to exclude a still greater reduction in information capacity and in mean frequency by requirements at subsequent branch points or junctions to succeeding relays. We are moving in the right direction, but not far enough as yet. There is therefore no reason to discard information theory as a guide to our research.
Thermodynamics has been useful in physics because there are many physical systems that maximize their entropy. Organisms that survive must be fairly efficient. It is natural therefore to suppose that the central nervous system, whose whole business is a traffic in information, maximizes the flow of information for its channel capacity. This may be a mistaken assumption. It may well be that some other cost of information, say for designing components or for assembling them, puts more stringent requirements upon the living system. Redundancy to exclude fatal error is obviously another requirement. Clearly we must be alive to all these possibilities, yet it would be worth while to try to put a lower bound on the information capacity of these input channels. We need to know the optimum code to employ when we are confronted with a kind of fading — worst at shortest intervals, and most disturbed by most nearly synchronous signals along most nearly parallel channels. This is a problem that we happily submit for solution to our friends, the information theorists.
Footnotes
For further research:
Wordcloud: Axons, Bound, Branches, Capacity, Channels, Coding, Column, Conditioning, Conduction, Connections, Cord, Diagram, Dorsal, End, Experiments, Far, Fig, Figure, Fire, Frequency, Impulses, Information, Input, Lines, Lower, Millisecond, Nerve, Nervous, Neurons, Per, Point, Produce, Receptors, Record, Region, Relays, Requires, Research, Resistance, Root, Short, Signals, Spike, Spinal, System, Theory, Think, Upper, Volley, Voltage
Keywords: System, Transmission, Information, End, Connections, Looms, Brain-Wise, Systems, Memory, Diagram
Google Books: http://asclinks.live/dck3
Google Scholar: http://asclinks.live/h090
Jstor: http://asclinks.live/4wn6