INVESTIGATION ON SYNAPTIC TRANSMISSION12 [108]
W. Pitts, J.Y. Lettvin, P.D. Wall and W.S. McCulloch
##
The central nervous system, like the heart, produces electrical signs of its action at body boundaries; but that these signs can be interpreted in terms of function tells more of the glory of nature than the ingenuity of biologists, for not by polarity height, frequency, or distribution is it possible to relate the potentials recorded on the surface to events within. No more useful are the records from single electrodes thrust into the nervous felt, except where they show the impulses of blocked fibers or butted cells. We can tell the firing of single cells or fibers and measure their frequencies, but the chaos of synapsis is less neatly handled, and it is this chaos to which most of the pen-wiggles are attributed.
There are three ways to get electrical information about the central nervous system. The first two are indirect, and have been largely exploited. One is to examine the input-output relations of the whole structure: the other is to use emergent fibers as electrotonic probes of events affecting their intramedullary extensions. The results of the former method are ambiguous, without detailed knowledge of the anatomy and physical properties of junctions. Morever, it is only rarely that the tracts entering or leaving a nucleus can be isolated well enough for separate stimulation and recording. The data provided by the latter method are susceptible of quantitative analysis only under most controversial assumptions, such as that the properties of the fiber do not change within the cord, even before their geometry is altered by bifurcation, demyelination, expansion, or coarctation. Accordingly, we have devised a third technique to examine activity in the central nervous system at the place where it is.
As you know, an impulse along a neuron is a region of depolarization, receiving current from an adjacent polarized membrane. This carries the impulse farther. If the neuron lies in a nonconductor, an electrode on one region pitted against a far-distant electrode perceives the potential of the local membrane with respect to the other; the passing impulse is seen as the familiar negative monophasic spike. But if the insulating medium is replaced by a conductor, such as electrolyte, the potential of the electrode is proportional to the current across the membrane, which is very nearly the second derivative along the neuron of the monophasic spike which would have been recorded if the neuron had been in oil. But it is attenuated because the electrode computes a weighted average over a volume of a function whose own average is zero. To this external medium, the nerve appears to produce, absorb, then produce current when a spike passes; from this probe’s standpoint of view, the impulse is a source, followed by sink, followed by source. Their algebraic sum in time is zero, unless the impulse stops either at the electrode or short of it. In the former case, the preceding source is averaged with the initial part of the sink, but the stationary decaying sink is recorded as a large negative potential with respect to a remote electrode. In the latter case, the electrode perceives only a source, near it, rising as the impulse approaches the block, then decaying as the impulse fades; it therefore turns monophasically positive. For this reason, it is possible to record single fiber activity in the central nervous system, when the micro-electrode blocks individual fibers. The recorded spikes may be either purely positive or positive and then negative. It is unnecessary to suppose that spikes are only recorded from cell bodies, since such records can be obtained from peripheral nerve with micro-electrodes. It is likely that some of the large potential swings recorded in synaptic regions are records of the impulses having reached the ends of presynaptic arbors.
Let us consider for a moment a parallel bunch of axons entering a bounded conductor in which it is blocked. The passage of the impulse is small to any boundary electrode: only the entry of the impulse into the volume and the dying dipole at the block are conspicuous. Mapping the potentials all over the boundary would hardly determine the point of entry and the place of block, since any distribution of potentials on the surface can be realized by an infinite number of widely different configurations of sources and sinks within. Unless we can narrow the choice enormously from additional knowledge we hardly ever possess, we can only speculate, as people do freely, apparently not realizing their temerity, where the disturbance lies. It is, in a word, impossible to infer the pattern of central nervous system activity from the most detailed surface measurements on cord or cortex, or from records at single points in the substance.
Sources and sinks in a volume conductor are strictly additive in their effects on the potential in the external medium. The potential at each point is a sum of contributions from all of the sources and sinks present at that time anywhere. Its magnitude and sign are consequently no direct indicators of elements active in the immediate neighborhood of a recording electrode. In principle, however, if the potential V is known in enough detail, the source density ρ can be inferred from it by the well-known equation of Poisson:
if R is a bulk resistance of the fluid medium, We therefore decided to

repeat Berry Campbell’s mapping of the potentials in the spinal cord after dorsal root stimulation, but in enough detail and under such conditions that it should be legitimate to employ Poisson’s equation, or an approximation to it, to compute ρ.
To examine the activity of the cord in its substance, it is necessary to introduce a grid of electrodes arranged densely enough at accurately known stations to make out the progress of activity in fine fibers and to take simultaneous records from this grid. We cannot do this, if only because the volume of electrodes would seriously disturb the cord if they were large enough to record the signals above noise level. But we have found that an isolated cord, whose degree of anesthesia, temperature, circulation, and oxygenation stay reasonably constant, keeps its input-output curves and micro-electrode records tolerably the same for a long time, suggesting that we may treat successive records for repeated constant stimuli as if they were simultaneous. Supposing this, we introduced micro-electrodes serially, penetrating by measured steps to a final station, recording at each step, where we cut them loose from the apparatus and left them in situ for later verification of position.
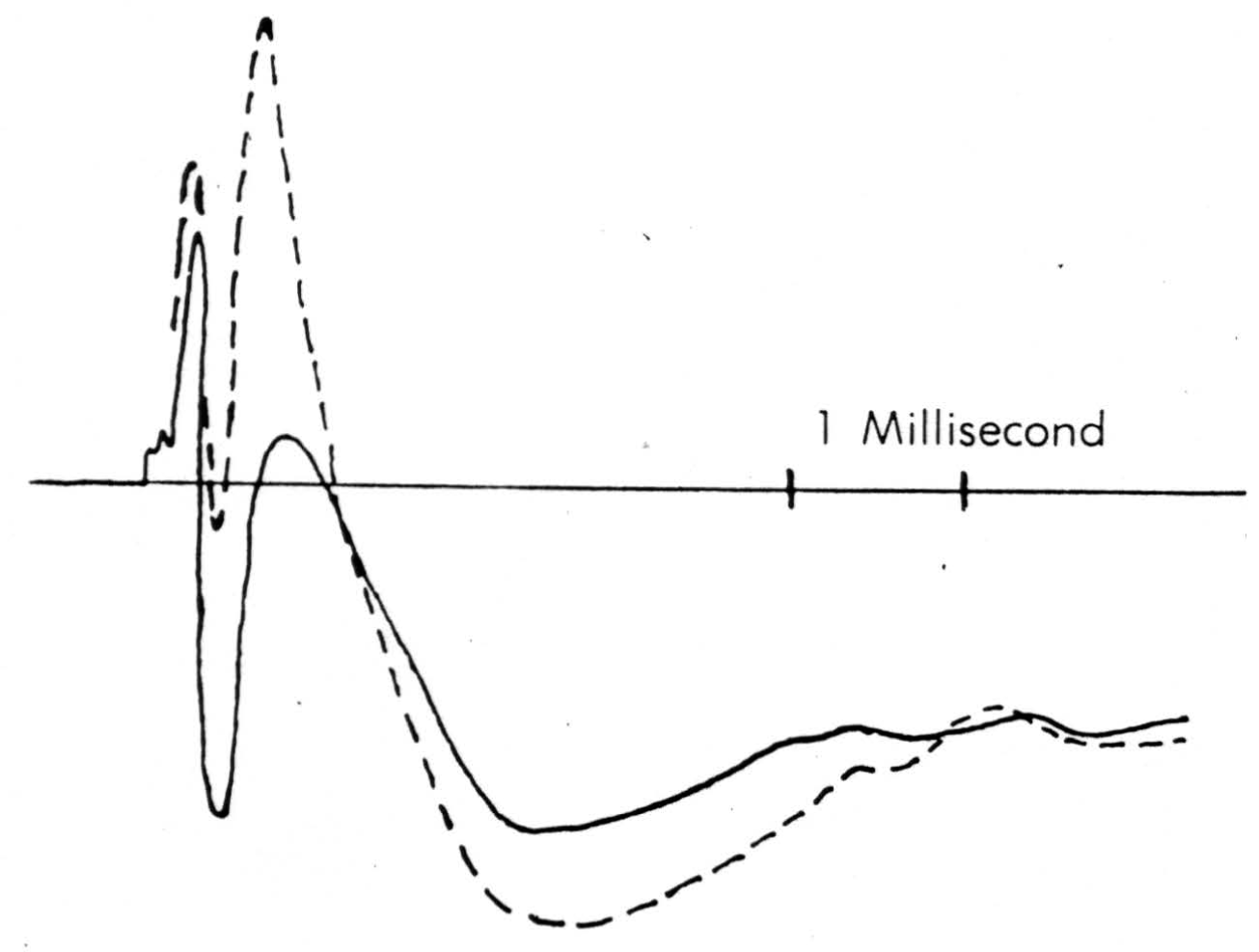
Figure 7. Solid line is record taken just touching surface of cord following a dorsal root volley. Broken line is record taken pressing electrode down to dimple the surface. The same stimulus has been used.
These micro-electrodes were spaced as closely as would not interfere with the monitored response in the ventral root, or about three per millimeter. Such a group is seen in Figure 6.
A detail of micro-electrode use is important enough to be mentioned here. It must penetrate easily and without dimpling the surface either on entry or further translation, for the cord is bounded by oil in these experiments and dimpling introduces serious errors by distorted surface reflections, as well as by pressure on neurons (as shown in Figure 7). This means it must have a microscopically smooth, sharp point, with no shoulder at junction with insulation and no change in shank diameter. These requirements are very necessary since we do not remove pia for fear of local damage. One such micro-electrode tip appears in Figure 8. Further, it must be small enough to minimize tissue damage, but not so small as to obscure the record with electrode noise. This critical diameter lies near 10 micra, the smallest wire it is possible to draw bare in most metals. A more extended discussion of electrode problems and properties will appear in a later publication. One further point deserves comment, and that is that withdrawing such an electrode through its own path introduces a distortion because of the reduced resistance of the track of destruction, an additional reason for considering only records taken on the way in.
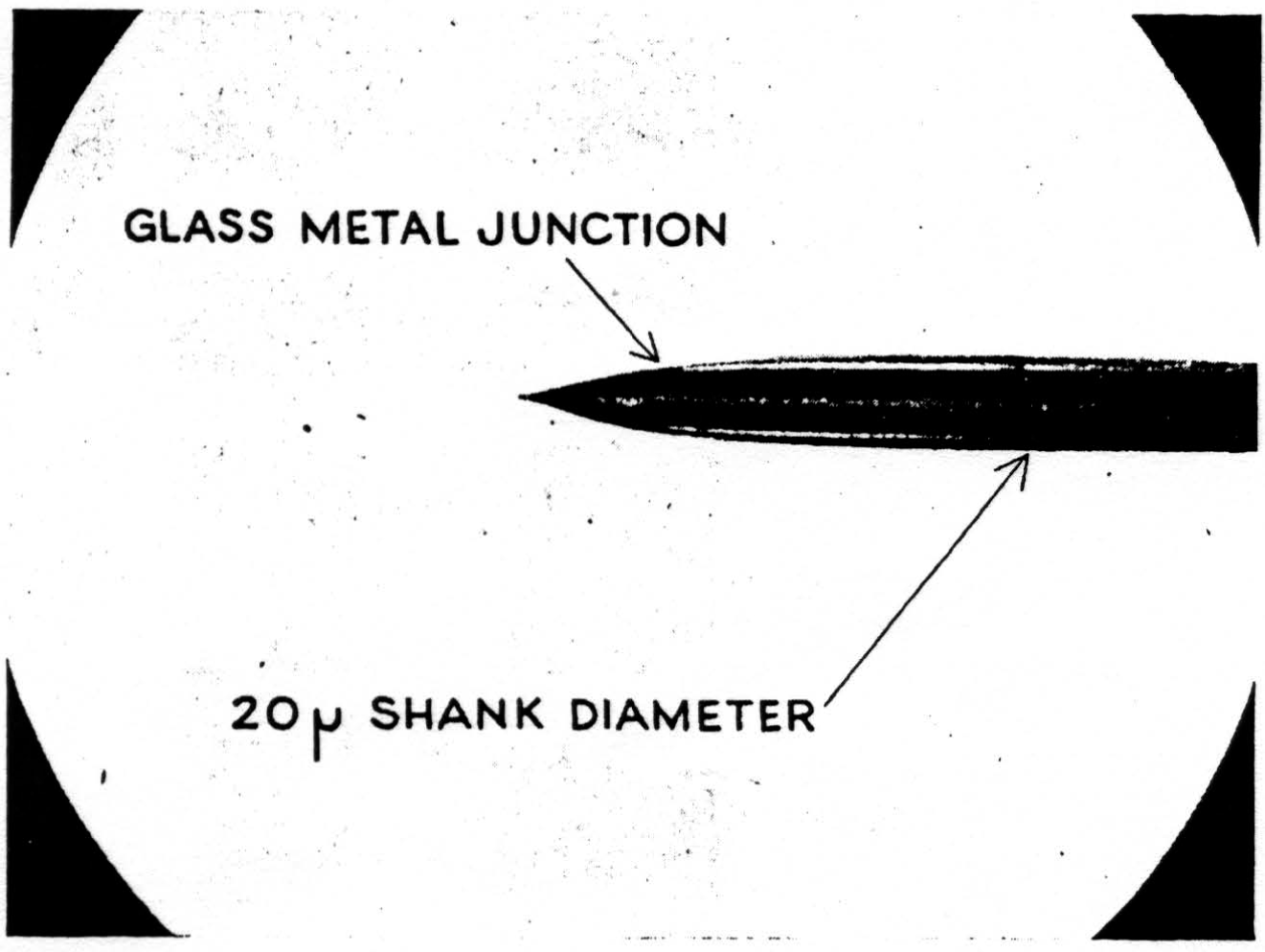
Figure 8.
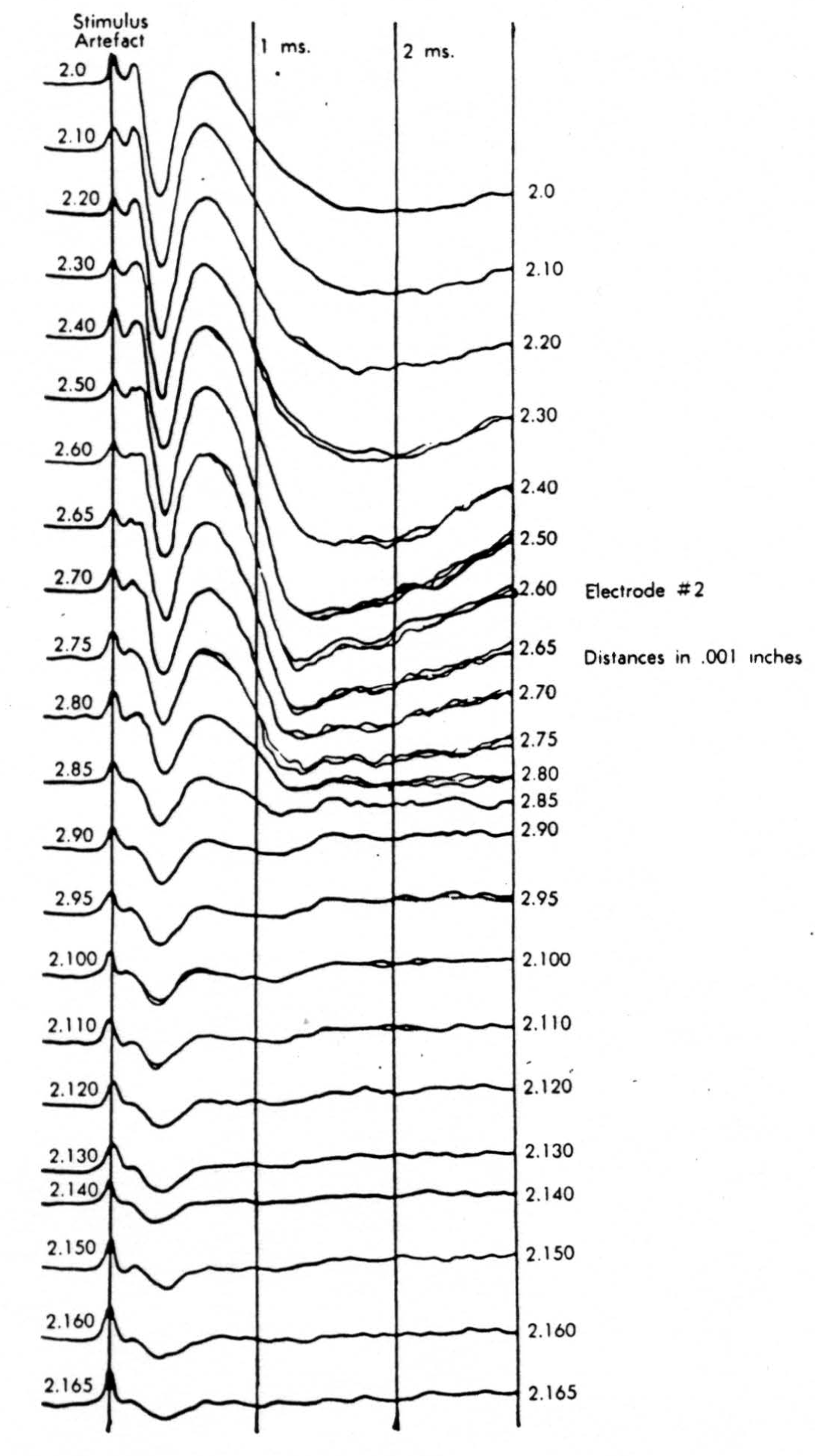
Figure 9.
In the experiment shown, we have used nine electrodes, giving a grid of about 300 points in 9mm2 of ½ of a transverse section of a segment adjoining that lumbar segment whose dorsal root we stimulated. Previous studies suggested that no great longitudinal currents flowed in the times we meant to consider, thus allowing us to record across a single plane. Figure 9 exhibits a sample of the records from one electrode track, three traces per position. The scatter for any one position is not excessive for computation. The spatial distribution of potential at one instant following the dorsal root stimulus is interpolated to a square lattice of about the same density, whence the LaPlacin can be approximated simply with a precision sufficient for the noise level. Naturally, since we interpret only differences (second differences, in fact) of potential, the position of the reference electrode is quite irrelevant. It might quite well be taken on the stimulated dorsal root. It does not matter whether it is “indifferent.” We are thereby also freed from specifying the position of the reference electrode. To present these records clearly, we filled a square around each computed value with the number of dots proportional to the value in arbitrary units, green for source and red for sink. In Figures 10 through 13, we present the isopotential map on the left and the source-sink map on the right for the successive times after dorsal root stimulus given in milliseconds in the upper left-hand corners. It is clear that the sources and sinks cannot be seen by simple inspection of the isopotential map.
Figure 14 is a drawing by Ramon y Cajal of the fiber distribution from dorsal root in the lumbar spinal cord of a newborn rat, whose white matter is thinner than appears in our section. While it is premature to push the anatomical interpretation of the records, let me remark on the set of fibers entering medially and curving back into the substantia gelatinosa. The series of maps shows a sink followed by source proceeding from the place where the fibers enter the gray matter at the base of the dorsal column, and moving laterally and then up into the substantia gelatinosa.
While the degree of resolution is coarse, and the noise of experiment, necessarily amplified by this kind of computation, is high, we think that this set of pictures shows more accurately than heretofore the places where activity occurs, how large it is, and in which direction it moves, in the cord of a spinalized cat anesthetized with Dial-cum-urethane. We mean to apply this technique to the problem of synaptic transmission.
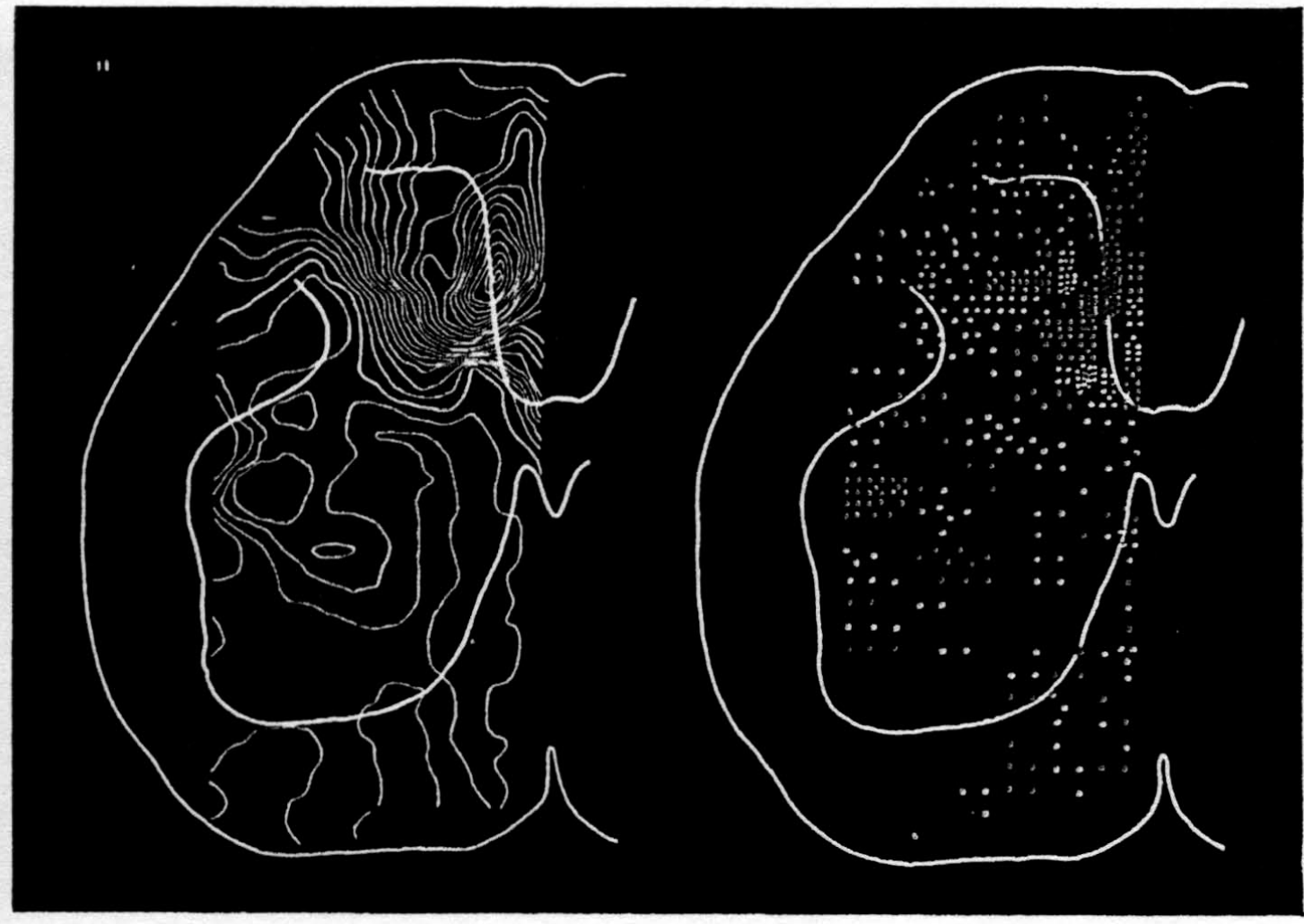
Figure 10.
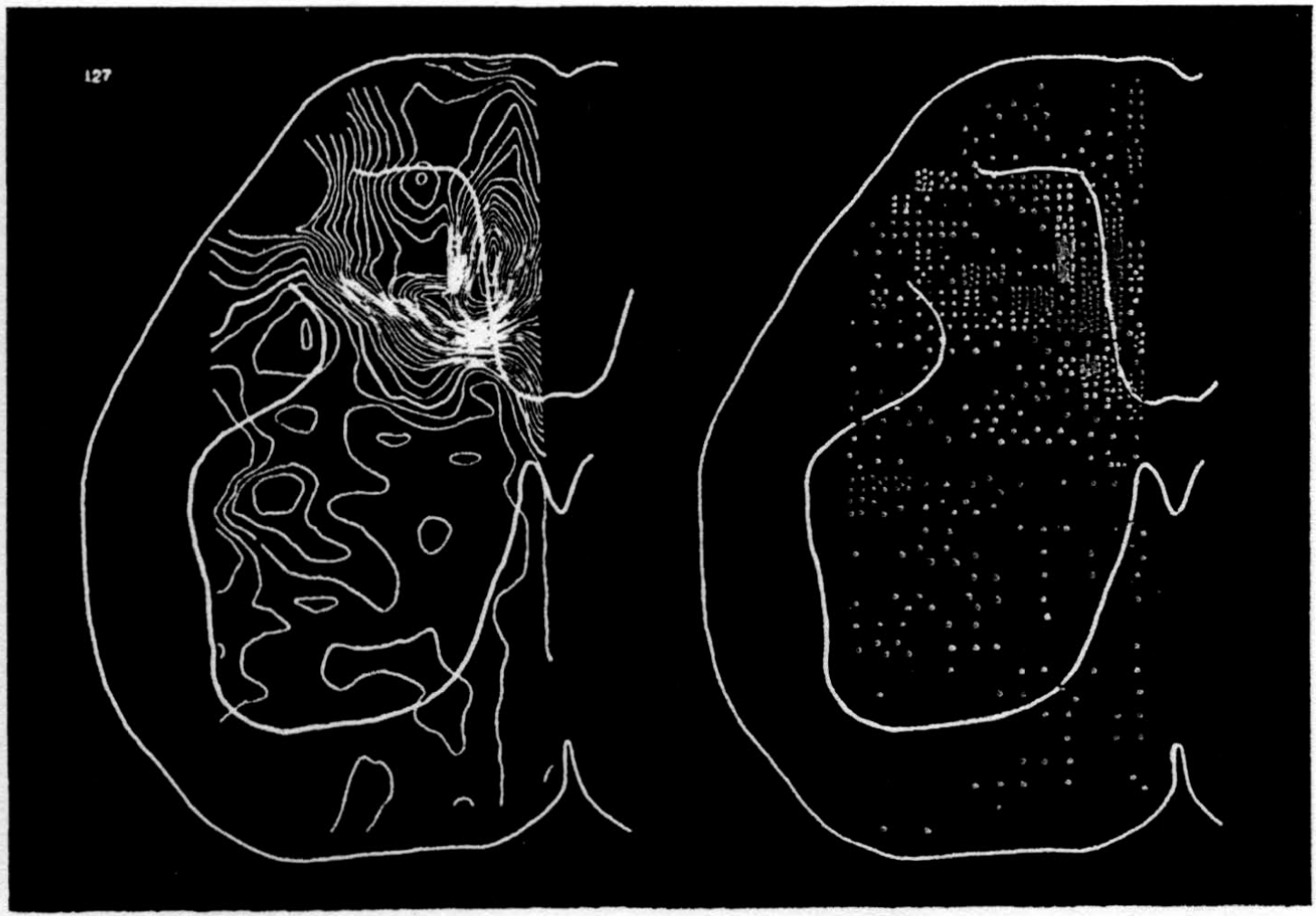
Figure 11.
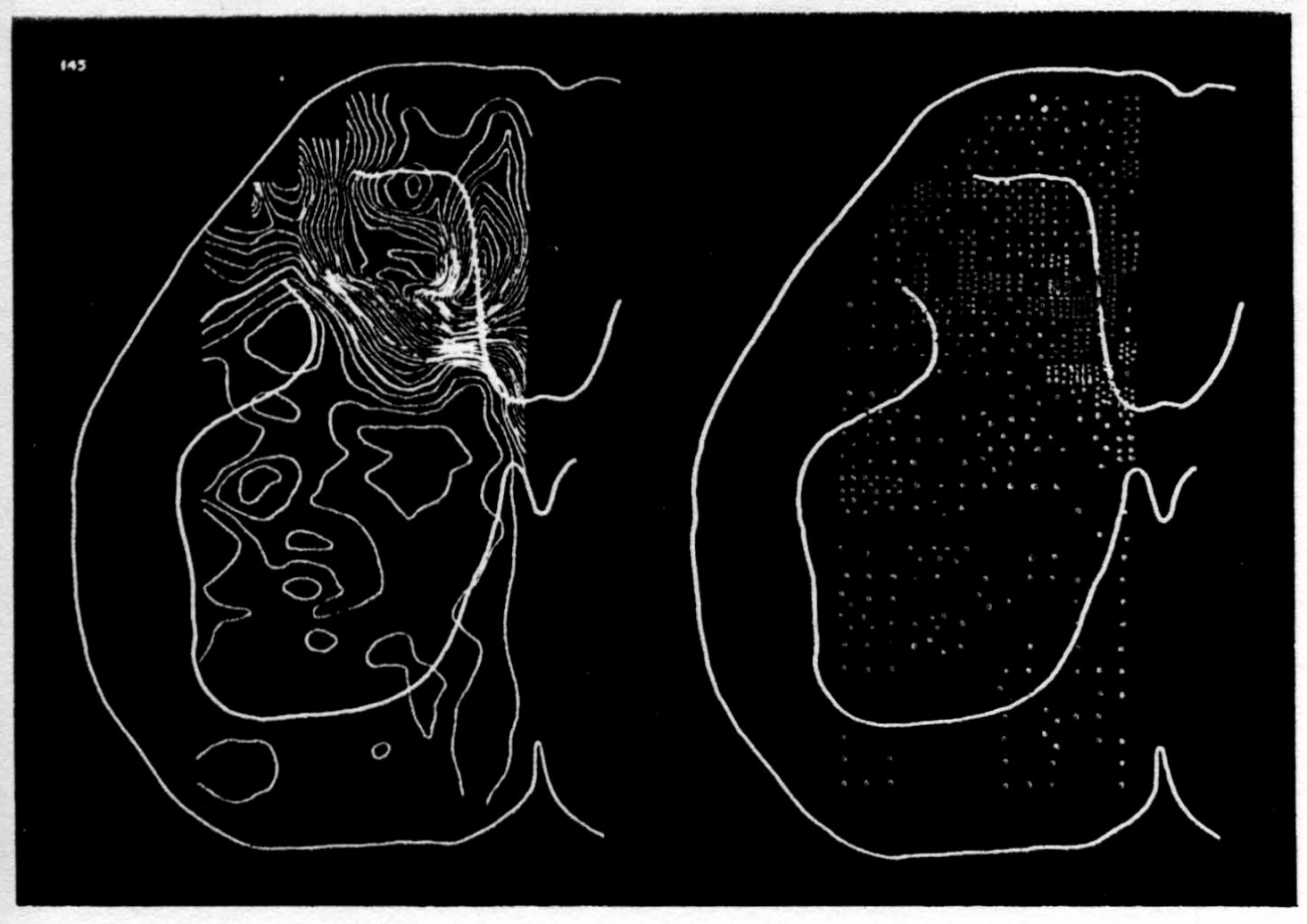
Figure 12.
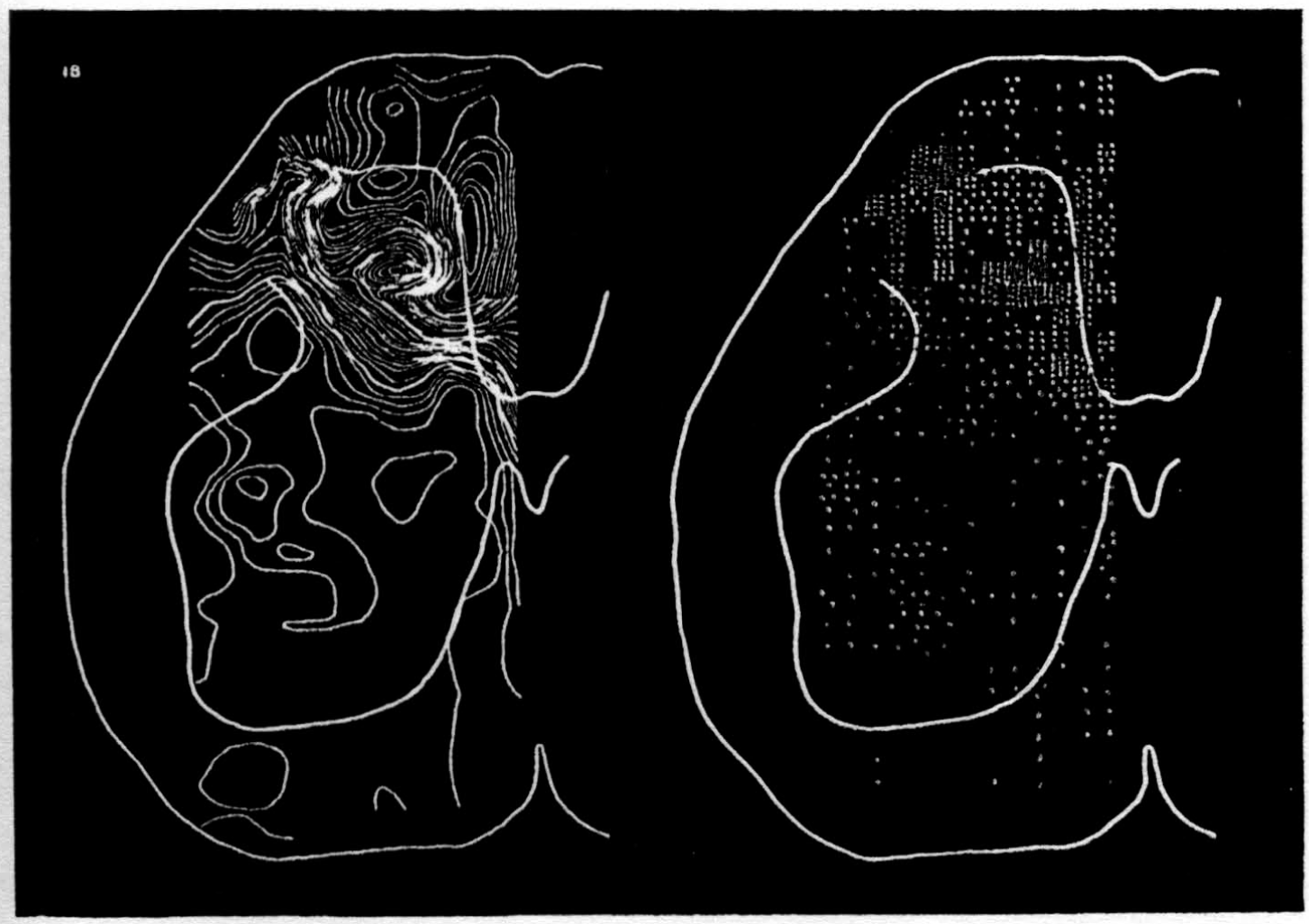
Figure 13.
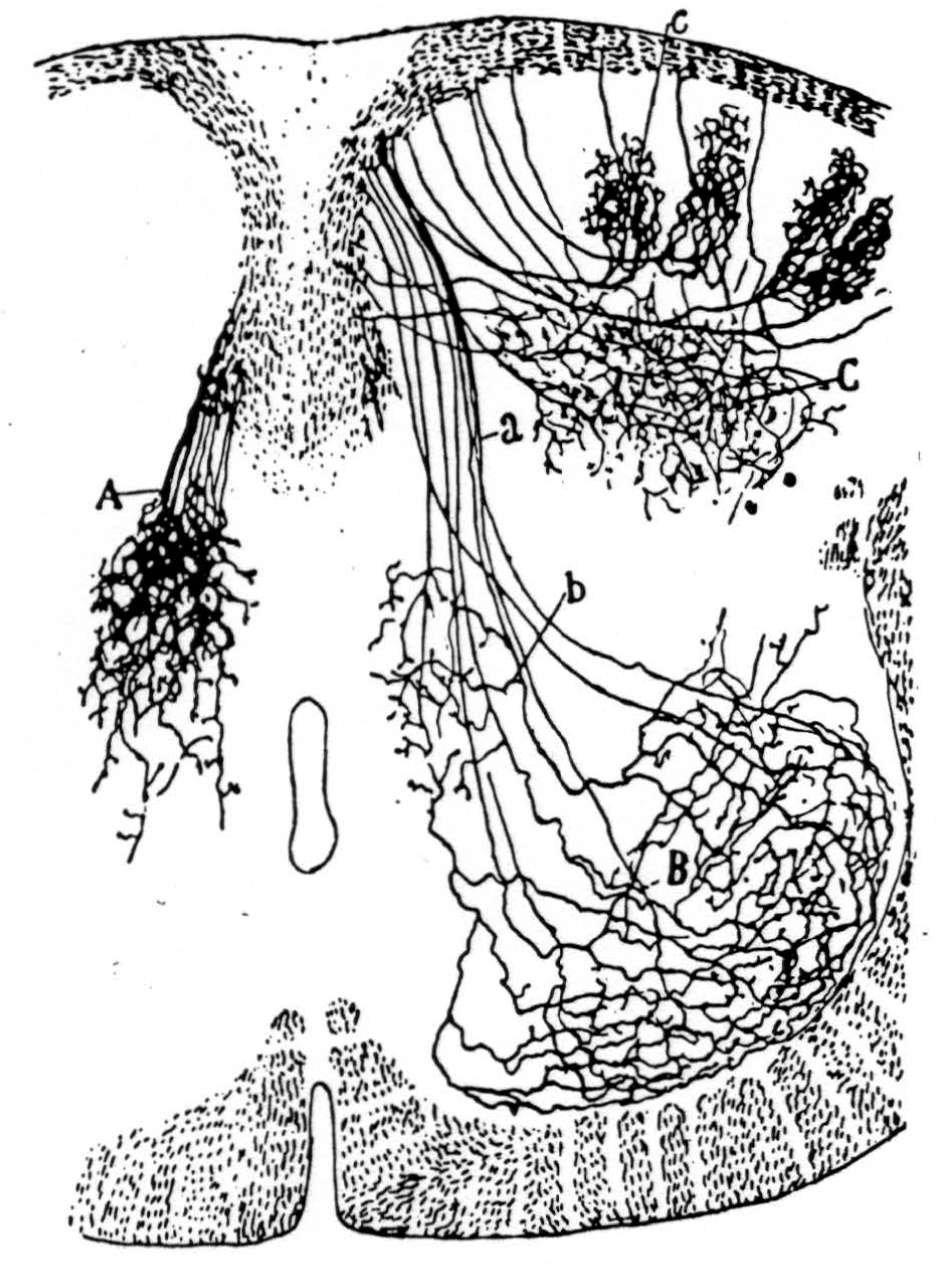
Figure 14. Principales collatérales sensitives, cheq le rat nouveau-né. Méthode de Golgi. A, collatérales du noyau gris intermédiaire; B, arborisations embrassant les noyaux moteurs; C, ramifications étendues dans la tête de la corne postérieure; a, faisceau sensitivo moteur, b, collatérales p fondes de la substance de Rolando. Reprinted by permission, from Ramon Y Cajal, S.: Histologie du Systéme Nerveux. Paris, Maloine, 1909.
Footnotes
For further research:
Wordcloud: Activity, Appears, Block, Central, Computation, Cord, Current, Delta, Detail, Dimpling, Distribution, Dorsal, Electrode, Enough, Entering, Fibers, Figure, Followed, Frac, Impulse, Introduces, Large, Map, Medium, Micro-Electrode, Monophasic, Nervous, Neuron, Noise, Point, Position, Potential, Produce, Records, Root, Signs, Single, Sink, Source, Spike, Stimulated, Substance, Surface, System, Taken, Volume, Whose
Keywords: Electrodes, Brain-Wise, System, Systems, Action, Maps, Link, Representations, Triumph, Boundaries
Google Books: http://asclinks.live/1hn1
Google Scholar: http://asclinks.live/r6se
Jstor: http://asclinks.live/5ayw