THE LIMITING INFORMATION CAPACITY OF A NEURONAL LINK1 [104]
D.M. MacKay and W.S. McCulloch
Abstract
The maximum rate at which a synaptic link could theoretically transmit information depends on the type of coding used. In a binary modulation system it depends chiefly on the relaxation time, and the limiting capacity equals the maximum attainable impulse rate. In a system using pulse-interval modulation, temporal precision may be a more important limiting factor. It is shown that in a number of typical cases a system of the second type could transmit several times more information per second through a synaptic link than a binary system, and the relation between relative efficiency, relaxation-time, and temporal resolving power is generalized in graphical form. It is concluded, not that interval modulation rather than binary modulation “ought” to be the mode of action of the central nervous system, but that the contrary assumption is unsupported by considerations of efficiency.
Introduction
The way in which the nervous system transmits information has long been the subject of debate. On the one hand, the all-or-none character of the nervous impulse and the demonstrated performance of motoneurons as coincidence detectors (1) led naturally first to a model of the central nervous system (2); (3) in which information was represented in terms of binary digits, quantized with respect to time as in a serially operated digital computer. On the other hand, there has been a steady accumulation of other evidence which has been adduced in favor of models (4) employing frequency modulation of trains of impulses to represent the information transmitted. We refer here not only to the long known fact that sense organs deliver trains of impulses whose frequency after adaptation is roughly proportional to the logarithm of the intensity of stimulation, but also more particularly to recent observations (5); (6) that the frequency of discharge of spontaneously active central neurons can be altered in response to signals afferent to them.
In view of these last observations and others like them, it seems realistic to consider how efficiently a typical neuronal link, or “synapse,” could be used to convey information in this way, and particularly to compare its limiting efficiency with that which could be achieved if it were used on the digital basis of the first model.
It is not to be expected that the proponents of either of these models believed them to be the whole story, nor is it our purpose in the following investigation to reopen the “analogical versus digital” question, which we believe to represent an unphysiological antithesis. The statistical nature of nervous activity must preclude anything approaching a realization in practice of the potential information capacity of either mechanism, and in our view the facts available are inadequate to justify detailed theorization at the present time. What does seem worth while at the moment is a sufficiently general discussion to determine upper limits of performance and so provide a quantitative background to lend perspective to the framing of hypotheses.
Selective information content
A signal is a physical event that, to the receiver, was not bound to happen at the time or in the way it did. As such, we may think of it as one out of a number of possible alternative events, each differing perceptibly in some respect from all the other possibilities. A given signal can therefore be considered as an indicator, selecting one out of a finite number of perceptibly distinct possibilities, and thus indicating something of the state of affairs at its point of origin. The greater the number of possible alternatives to a given signal, the greater the “amount of selective information” we say it contains. The selective information-content of a signal is in fact defined as the logarithm (base 2) of the number of alternatives, where these are all equally likely a priori. This simply represents the number of steps in a search process among the alternatives carried out in the most efficient way—by successive subdivision of the total assembly into halves, quarters, and so forth. (We shall not consider the case of unequal prior probabilities.)
Now a neuronal impulse carries information, in the sense that it indicates something of the state of affairs at its point of origin. It is able, moreover, on arriving at an axonal termination, to affect the probability of occurrence of an impulse in the axon of the cell with which it “synapses.” Thus, whatever else does or does not “cross a synapse,” it is safe to say that information does. The nature or even the existence of the synapse as a physical link is not here in question. For our purpose it will be sufficient to consider the observable time-relations which obtain between incoming and outgoing impulses in cases in which these are temporally coherent. These will enable us to estimate the upper limits to the information capacity of such synaptic links—the maximum number of “bits” carried per second—and to compare the informational efficiencies of the different modes of operation (called modulation systems by the communication engineer) which are conceivably available to model makers of the C.N.S.
In particular we shall examine the suggestion that an all-or-none binary code using pulses separated by minimal quantized time intervals would be more efficient than a system using the same elements in which the varying time of occurrence of impulses represented the information to be conveyed. This does not appear to be the case.
The selective information-content of an impulse
To determine the limiting information-content of a signal, we have to decide (a) which parameters are permissible variables, (b) how large a variation must be in order to be perceptible, or rather to be statistically significant, and hence (c) how many significantly distinct values of each parameter are possible. We ought also to know (d) the relative probabilities of the different possible combinations of parametric values, if these probabilities are unequal; but unless their differences are great the order of magnitude of the information content will not be affected. (The effect will always be a reduction of the average information-content per signal.)
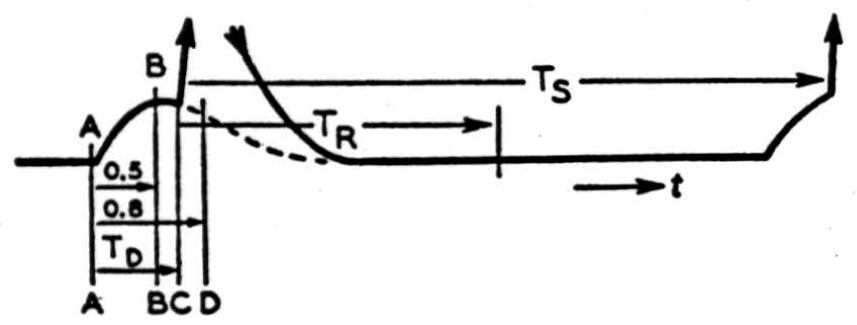
Figure 1.
The limiting selective information-capacity of a signal-carrying element will then be the product of the average information-content per signal, with the maximum mean signal-frequency allowable for the modulationsystem adopted.
Typical time-relations which have been observed in so-called synaptic transmission are summarized in Figure 1.
An afferent impulse which begins to rise at A may give rise to a spike (of about 1 msec, in duration) at any time C between B and D, 0.5 to 0.8 msec, later. The majority of spikes, however, are observed to occur after an interval, the “synaptic delay,” TD, with a standard deviation of less than 0.05 msec., and a typical mean value of the order of 0.65 msec. (7). '
No matter how high the frequency of stimulation, successive spikes are not observed to occur within time intervals Ts of less than 1 msec. Frequencies of 500 per second are not long sustained, and a reasonable upper limit for a steady response to recurrent stimuli would perhaps be 250 per second. In central auditory nerve fibers for which unfortunately no constants of monosynaptic transmission are available to us, maximum frequencies, after adaptation, of 250 to 300 c/s have been observed (8). There is thus a minimal “dead time” TR between impulses which ranges from 1 to 4 msec., according to the demands made on endurance.
Now the amplitude of a nerve impulse is relatively slowly variable, and the total amount of information conveyable by such variation would be relatively small. For our purpose we shall assume that the amplitude can have only two values, namely, zero or unity on an ad hoc scale. Thus each impulse, simply by its presence or absence during the short period over which it was expected, could provide one unit or “bit” of selective information. If, therefore, we had a system in which we “quantized” the time scale by dividing it into discrete intervals equal to the minimum necessary separation TR between impulses, the system should on the above basis be able to convey 1 /TR bits of information per second at most. Such a system we may call a time quantized binary system (2).
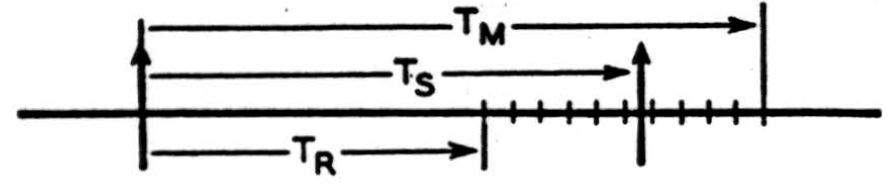
Figure 2.
There is, however, another variable parameter of our neuronal signal. The time interval between successive impulses can vary, so that any given interval represents a choice out of a certain range of possible pulse positions on the time axis. Let us denote by Ts the time interval between one pulse and its immediate predecessor (Fig. 2), and suppose that for reasons which we consider later Ts has a maximum permissible value Tu, and of course a minimum TR. The range of Ts, (TM − TR), may be thought of as subdivided into a finite number of equal intervals, of magnitude ΔT.
These intervals must not be smaller than the average fluctuations in TD (Fig. 1) if changes in Ts are to be statistically significant, and we may conveniently assume at first that they are of the order of 0.05 msec. (1). We thus think of our impulse as selecting, by its occurrence at Ts, one out of (TM - TR)/ΔT possible positions on the time axis. Calling the ratio (TM−TR)/ΔT, n, we have here log2 n bits of selective information per signal, in respect of its instant of occurrence.
Now for maximum efficiency our hypothetical system should on an average use all n possible values of Ts equally frequently. The mean value of TS will therefore at maximum efficiency be ½(TM + TR). A “pulse interval modulation” system could evidently convey in this way a maximum of
bits of information per second.
It is here that we find a criterion for the optimum value of TM. Clearly if TM is allowed to increase indefinitely, the number of bits per impulse also increases indefinitely—but only roughly as the logarithm of TM,whereas the number of impulses per second goes down roughly as the inverse of TM itself. The optimum value of Tu is that which maximizes
If we take ΔT as our unit of time, writing TM = mΔT and TR = rΔT, we have
This is maximum for a given r when
Taking a value of 1 msec, for TR and 0.05 msec, for ΔT, we find by approximate solution of (3) that at TM = 2 msec, a maximum selective information capacity of about 2.9 bits per msec, could theoretically be be attained, as against 1 bit per msec, on the binary quantized system. Under these conditions the mean frequency would be about 670 impulses per second and the average information content about 4.3 bits per impulse.
First approximations to realism
Our discussion hitherto has been mainly academic. We have seen that a communication engineer could use an element with the properties idealized in Figure 1, nearly three times as efficiently in a pulse-interval modulation system as in a binary system at the maximum possible pulse frequency. We have favored the latter as much as possible by (a) granting a maximum frequency of 1000 per second; but (b) we have not yet asked whether the precision of timing between stimulus and outgoing impulse is matched by a corresponding precision of time-resolution in possible receiving centers; (c) we have not considered the possible increase in the variance of synaptic delay due to irregularity in the pulse sequence; and (d) we have assumed all values of the modulated pulse-interval to be equally likely, irrespective of the position of its predecessor. This last assumption is valid in an estimate of limiting capacity.
In other words, our computation is probably not too unrealistic as an estimate of the maximum number of bits per msec., or even per 10 msec., which could be represented by the physical behavior of the signal. But for an estimate of the information effectively carried we must, as we saw above, consider the number of possibilities distinguishable by the receiver; and for an estimate of continuous information-capacity we must accept a lower value for the mean impulse-frequency.
Information on points (b) and (c) is scanty. It is known (Lorente de No, loc. cit., p. 422) that the period of latent addition of two converging impulses, over which their relative arrival-time may vary without appreciable effect, is of the order of 0.15 msec. This might seem to suggest that our scale unit of time ΔT should be of the same magnitude, or even twice this, since the relative delay may be of either sign. But the index of latent addition falls off very sharply over a few hundredths of a millisecond when the relative delay exceeds 0.15 msec. As a time resolving instrument, therefore, such a summation mechanism can in principle detect coincidence to much finer limits (as may be seen by imagining a constant delay of 0.15 msec, to be introduced into one signal path), so that it is not obvious that the operational value of ΔT merits much increase.
Not much more is known about the effects of irregular firing on synaptic delay. A range of 0.4 msec, is given by D. Lloyd (7) as the difference between the delay measured for a relatively refractory neuron which had just fired, and that for a relatively excitable neuron receiving summating impulses. In the case we have considered above, which is relatively least favorable to interval modulation, the interval between successive pulses might vary from 1 msec, to 2 msec, and might reasonably be expected to affect synaptic delay by perhaps 0.1 to 0.2 msec.
Let us suppose for a moment that in the worst case an imprecision ΔT of 0.3 msec, had to be accepted, and that we again tolerate a minimum pulse to pulse interval of 1 msec. The same calculation as before shows that at the optimum value of TM around 3.1 msec., an average information capacity of some 1.4 bits per msec, would be attainable, so that even under these extreme conditions a binary system would still be less efficient than the other by 40 per cent.
We must, however, make a further step toward realism by estimating the capacities for a higher value of the refractory period TR. Taking a frequency of 250 per second as reasonably attainable after adaptation (Galambos and Davis, loc. cit.) we can set TR = 4 msec, as perhaps a typical “adapted” value. We then find that when ΔT = 0.05 msec, the optimum value of TM is 6.6 msec, and the optimum mean frequency 190 per second, yielding as much as 1090 bits per second or nearly 6 bits per impulse. (At the maximum possible rate of 250 per second the corresponding capacity on a digital basis is of course only 250 bits per second.) Even if ΔT must be as large as 0.3 msec., a capacity of 620 bits/ sec. can be attained at TM = 8.6 msec, and a mean frequency of 160 per second—still 2 1/2 times the maximum capacity of the same element used in a binary system. Figure 3 shows in general how the ratio of the information capacity with interval modulation (CT) to that with binary modulation (CB) varies with the ratio TR/ΔT.
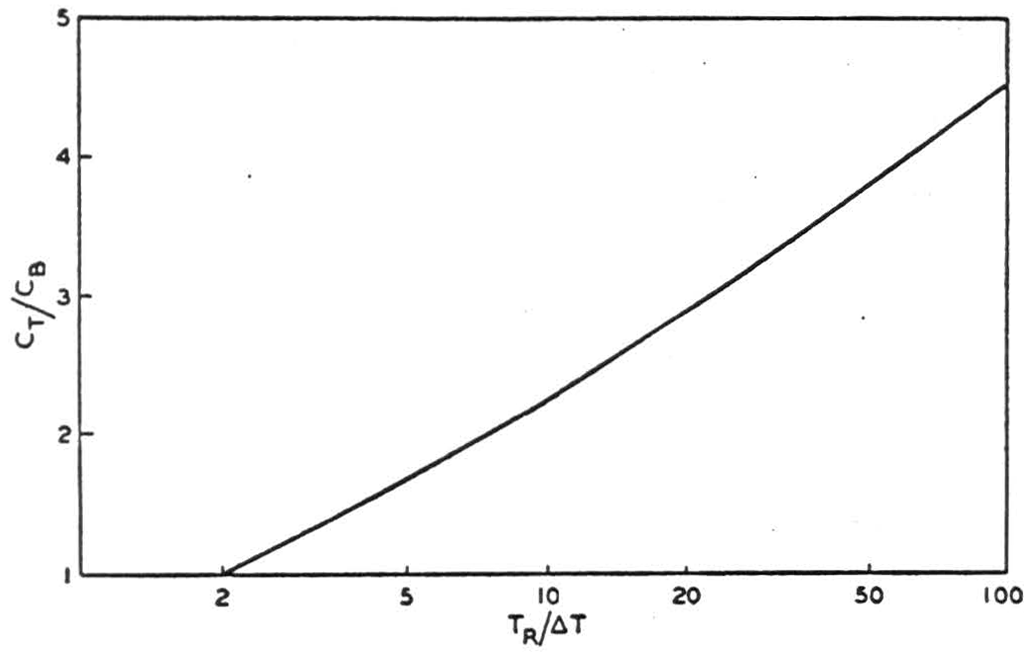
Figure 3. Relative efficiency of interval and binary modulation
Turning finally to consider normal as opposed to optimal conditions, we may take 50 impulses per second as a typical mean frequency of excitation of sensory fibers when transmitting information. Our calculation is now straightforward. A mean pulse to pulse interval of 20 msec, could correspond roughly to a minimum TM of (let us say again) 4 msec., and a maximum of 36 msec.—a range of 32 msec. Each impulse then selects one out of 32/ΔT possible positions, so that if ΔT were taken as 0.05 msec., the selective information content of each impulse would be log2 640 or about 9.3 bits per impulse, giving an information capacity of just under 500 bits per second despite the low impulse repetition frequency.
In general if a different value be taken for ΔT, say k times greater (TM and TR remaining the same), the effect is to reduce the selective information content per impulse by log2 k. Thus an increase of ΔT to 0.2 msec, allows only 7.3 bits per impulse; an increase to 0.4 msec., 6.3 bits, and so on. It should be noted, however, that these are figures for a fixed value of TM and are not the maximum figures for each value of ?*T, *which would be determined by optimizing TM as in the preceding sections.
It is of course exceedingly unlikely in practice that successive impulse positions would be statistically uncorrelated in these cases where so large a percentage change is theoretically possible in successive pulse intervals. It should be noted moreover that we have considered only one synaptic link. If a number of these were connected in series, the precision of timing would of course diminish, roughly as the square root of the number of links. Our qualitative conclusions should hold however for reasonably large multisynaptic links, since, as shown in Figure 3, the interval modulation system does not become inferior to the binary until ΔT exceeds TR.
V. Conclusions. Our discussions have here been concerned with the limiting capacity of a neuronal link as a transducer of information. We have seen that the observed time-relations between incoming and outgoing impulses indicate a precision that would justify the use of pulse interval or “frequency” modulation rather than binary all-or-none amplitude modulation in a communication system using such a transducer.
At the maximum pulse frequency normally attainable, the binary system would be inferior to the other by a factor of 2 or 3 at least. At the typical peripheral frequency of 50 per second, the theoretical factor in favor of interval modulation rises to 9 or more. Little significance is attached to the precise figures obtained, but they indicate the theoretical possibility that a maximum of between 1000 and 3000 bits per second could be transferred at a synaptic link.
It appears to the writers at least that the question is still mainly of academic interest. Its discussion must not be taken to imply a belief that either binary coding or pulse-interval coding in the communication engineer's sense are the modes of operation of the central nervous system. Much more likely is it that the statistically determined scurry of activity therein depends in one way or another on all the information-bearing parameters of an impulse—both on its presence or absence as a binary digit and on its precise timing and even its amplitude, particularly on the effective amplitude as modified by threshold control, proximity effects and the like. If cerebral activity is the stochastic process it appears to be, the informationally significant descriptive concepts when once discovered seem likely to have as much relation to the parameters defining the states of individual neurons, as concepts such as entropy and temperature have to the motions of individual gas molecules—and little more.
Perhaps the most realistic conclusion is a negative one. The thesis that the central nervous system “ought” to work on a binary basis rather than on a time-modulation basis receives no support from considerations of efficiency as far as synaptic circuits of moderate complexity are concerned. What we have found is that at least a comparable information capacity is potentially available in respect of impulse timing—up to 9 bits per impulse in the cases we considered—and it seems unlikely that the nervous system functions in such a way as to utilize none of this. It is considered equally unlikely that its actual mode of operation closely resembles either form of communication system, but this quantitative examination may perhaps serve to set rough upper limits and to moderate debate.
Literature
Lorente de Nó, R. 1939. “Transmission of Impulses through Cranial Motor Nuclei.” Jour. Neurophysiol., 2, 401-64.
McCulloch, W. S. and W. Pitts. 1943. “A Logical Calculus of the Ideas Immanent in Nervous Activity.” Bull. Math. Biophysics, 5, 115-33.
Pitts, W. and W. S. McCulloch. 1947. “How We Know Universals.” Bull. Math. Biophysics, 9, 127-47.
Lashley, K. S. 1942. “The Problem of Cerebral Organization in Vision.” *Biological Symposia,’ *VII. Lancaster, Pa.: Jacques Cattell Press.
Brookhart, J. M., G. Moruzzi, and R. S. Snider. 1950! “Spike Discharges of Single Units in the Cerebellar Cortex.” Jour. Neurophysiol., 13, 465-86.
Gernandt, B. 1950. “Midbrain Activity in Response to Vestibular Stimulation.” Acta Physiol. Scandinavica., 21, 73-81.
Lloyd, D. 1946. Fulton: Nowell's Textbook of Physiology, pp. 140-41. Philadelphia and London: W. B. Saunders Company.
Galambos, R. and H. Davis. 1943. “Response of. Single Auditory Nerve Fibers.” Jour. Neurophysiol., 6, 39-59.