MACHINES THAT THINK AND WANT1 [95]
W.S. McCulloch
Introduction
Some twenty-five years ago I left philosophy and turned toward psychology hoping to answer but two questions: First, how do we know anything about the world—either its particulars as we apprehend events or its universale as we know ideas? Second, how do we desire anything—either physically, as we want food and drink or a woman and a bed, or mentally, as we seek in music the resolution of a discord or, in mathematics the proof of a theorem? From psychology I turned to physiology for the go of the brain that does these things. Twenty ideas that came but one a year can be said in twenty minutes because they spring from traits of neurons in simple circuits.
Think of a neuron as a telegraphic relay which, tripped by a signal, emits another signal. To trip and to reset takes, say, a millisecond (1). Its signal is a briefer electrical impulse whose effect depends only on conditions where it ends, not where it begins. One signal or several at once may trip a relay, and one may prevent another from so doing (2, 3). Of the molecular events of brains these signals are the atoms. Each goes or does not go. All any neuron can signal to the next is that it was tripped, but, because it signals only if tripped, its signal implies (4) that it was tripped. Thus the signal received is an atomic proposition. It is the least event that can be true or false (5). If it is unnaturally evoked it is false, like the light you see when you press on your eyeball. How you find it false is another question (4).
Of two possible atomic events there are four cases, each shown by putting a dot into one of 4 places in an X—A happens, place dot on left; B, right; both, above; neither, below. Every next atomic avent, depending on two present atomic events, is shown as a dotted X of which there are 16, being all the functions of the calculus of propositions. The first, with no dots, shows the signal of a neuron never tripped—call it contradiction; and the last, with 4, the signal of one tripping itself every millisecond—call it tautology. Only the upper row of functions go in nets without tautology, for a dot below the X, showing the signal of a neuron neither of whose atomic propositions had come, is the signal of a neuron untripped. Give signals only two actions—one tripping, one preventing—and still nets of few neurons channel all these functions (5). Moreover, we could replace nets of neurons modified by use by changeless nets of changeless neurons (5), and these functions do not depend on modes of tripping or preventing atomic propositions (6)—hence the purview of this calculus.
To the psychologist this is most important, that such nets of neurons can compute any computable number (5).
The logical probability (7) of each of the 16 functions is the number of dots for separate signals divided by the number of possible places, which is 4. For the a priori probability that a neuron is in a particular state is ½ i.e. 2-1, and that n independent neurons are in a particular state is ½n, i.e. 2-n. One unit of information defines the state of one neuron, so n units, the state of n neurons—hence the amount of information is the logarithm of the reciprocal of the probability of the of the of the state If in a particular millisecond we are given an Ẋ, since its probability is 1/4, its amount of information is 2 units. But the frequency of realizing Ẋ from independent signals is the product of their separate frequencies. Hence, averaged through time, Ẋ will transmit no more information than its afferent neurons singly. Similar considerations apply to all functions. So n independent neurons, regardless of their functions, transmit on the average n units

Figure 1.
of information per millisecond. Moreover, n neurons can be in any one of 2n states in one millisecond and in 2nt, in t milliseconds. So, in p milliseconds one neuron can transmit as much information as p neurons in one millisecond (5). Information measures the order of an ensemble in the same sense that entropy measures its chaos (8). In Wiener's phrase, information is negative entropy; and in our X's the more the dots the greater the entropy.
Neurons can be exchanged for milliseconds, and functions of greater for those of less logical probability, but we cannot get out of the brain more information than went into it. We express much less, because a nerve of a thousand axons has 21,000 possible states—which is more than there are particles in the universe,— whereas the muscle it drives has a paltry thousand possible tensions.
On the receiving end we reject far more information. Consider the eye. Each of its hundred million rods and cones may at one moment fail to fire with much light, and at the next, fire with almost none (9). If this be by chance it may be ignored in large groups of contemporaneous impulses. We detect the agreement of these signals by their coincidence on the ganglion cells and relay only that information to the brain. Thus we pay for certainty by foregoing information that fails to agree with other information. No machine man ever made uses so many parallel channels or demands so much coincidence as his own brain, and none is so likely to go right. Similarly, our hypotheses should be so improbable logically that, ü they are instanced, they are probable empirically.
Because light falling on a rod may or may not start a signal, that signal implies —but only implies (10, 7)—the light. If a bipolar cell is tripped by the rod's signal, then the bipolar's signal implies the rod's signal, and it, in turn, the light. Similarly a signal by a ganglion cell implies the bipolar, the rods, and so the light. Thus what goes on in our brains implies—but only implies—the world given in sensation. The domain of these implications extends only backward in time. Wherefore we know only the past. These bounds are proper toxognition. If each neuron were to signal when and only when it had received one of several signals, we could proceed in the opposite direction from brain to muscle, with every step an implication. The present would imply fate as well as fact. We could then deduce our deeds from our thoughts and our thoughts from our sensations. Rather this is the nature of intention; that it falls short of implication to the extent that aught intervening thwarts us. Perforce we discern that we will from that we shall do. Such bounds are proper to conation.
Now a signal anywhere implies an event at just one past moment unless there ie a loop it may circuit (4). Once started in a circle it implies an event at any past time which is a multiple of the period of the circuit. A set of such signals, patterned after some fact, as long as its figure endures, implies a fact of that form. This form-out-of-time is an eternal idea in that temporary memory which generates objects new in our world; for it recognizes them on first acquaintance (11). But these fleeting figures people only the specious present, and when the brain rests (12) they are no more anywhere. The aged often have no other memory (13); but in young brains, use leaves a trace whereby the ways that led us to our ends become ingrained. We must make and read our record in the world. This extends the circuits through our heads beyond our bodies, perhaps through other men. Records are not signals, but may start them again in the old figure. To them as well our calculus applies, enriched by ideas, or timeless objects, attributed to some or all events (5); for all forms of memory other than reverberations are but their surrogates (4). Man-made computers store information as arrays of jots and tittles only to regenerate signals in artificial nets of relays and so recall the past. For this the right array must first be found, then recognized; and, when the information is in divers arrays, it must be reassembled, or, as we say, remembered. Thus, over all, the procedure remains regenerative—a positive feedback.
Circuits with negative feedback return a system toward an established state which is the end in and of the operation—its goal (14). Reflexes left to their own devices are thus homeostatic (15). Each, by its proper receptors, measures one parameter of the body—a temperature, pressure, position, or acceleration—and returns that parameter to its established value. Similarly, within the brain, impulses through the thalamus to the cortex, descending from its suppressor areas indirectly to the thalamus, inhibit it, and so govern the sensory input as to extract its figure from its intensity (16),(17),(18). If such circuits are sensitive enough they oscillate at their natural frequency. Their response depends on the time the returning meet the incoming signals, and at some frequency of excitation they will resonate; but another circuit, responding to the derivative of excitation, will check that resonance.
Clerk Maxwell first computed the go of the governor (fig. 2) of a steam engine (19). It had two balls hung from the top of a vertical shaft turned by the engine. When
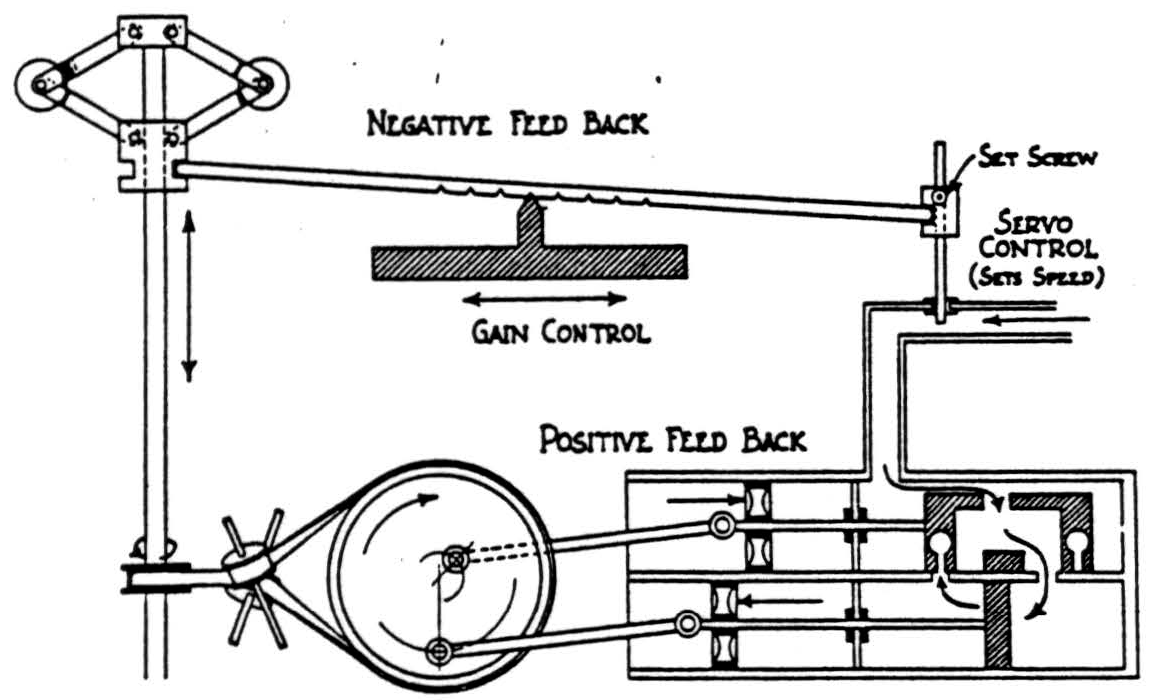
Figure 2.
speed increased they flew out, pulling up one end of a lever on a movable pivot, and so, by an adjustable link, throttled the engine. Moving the pivot changed the sensitivity, which we call the gain of the circuit; but changing the length of the link set the speed at which it was to run, regardless of load or head. Compared to the change in work the engine makes, that to set the link is negligible but its information all important, and we call this a servo-mechanism (20). The stretch reflex is one in which the length the muscle will attain is selected by the brain for its own ends. Such government by inculcation of well-chosen values of ends sought by the governed works wonderfully well.
Purposive acts cease when they reach their ends. Only negative feedback so behaves and only it can set the link of a governor to any purpose (21). By it, we enjoy appetites, which, like records that extend memories, pass out of the body through the world and returning stop the internal eddies that sent them forth. As in reflexes, the goals of appetition are disparate and consequently incommensurable. They may be as incompatible as swallowing and breathing; and we are born with inhibitory links between the arcs of such reflexes. But of appetitions the dominance is rarely innate or complete, and we note the conflict whose outcome we call choice. When two physically or psychologically necessary acts are incompatible, “God” cannot forgive us for not doing the one because we must do the other. The machine inevitably goes to hell.
Of any three circuits subserving appetition the dominance may be circular (22). I have myself encountered this in aesthetics; for, of three very similar rectangles shown in paired comparison, the first was consistently preferred to the second, the second to the third, and the third to the first, on the average and by the single subject. I discarded the data as inconsistent, whereas it bespoke consistency of a kind I had not dreamed of. We inherit from Plato a vain superstition called “the common measure of all values.” These are not magnitudes of any single kind, but divers ends of divers circuits so interconnected as to secure dominance which, like as not, is circular. Economic arguments from curves of indifference and attempts to set up one scale for the strength of drives for food, water, sex, and whatnot are fantastic ways to beget a gratuitous headache.
Negative feedbacks run through a series of affairs until they come to their ends. We have mentioned the automatic volume-control of somaesthesia (18, 16, 17). The pupillary reflex does the same for vision. An appetitive circuit can reduce whatever confronts it through a series of transformations to one so geared to our output that we cry “Aha!” We transform the Pythagorean Theorem, by legitimate steps, to the axioms and postulates which are the canonical form of such theorems. Similarly, we translate an apparition anywhere in the visual field to the center by turning our eyes in its direction. This reflex goes from the eye to the superior colliculus which, by double integration, determines the vector for the motor nuclei so as to turn the eye toward the center of the apparition. The integral decreases to zero as the eyes come to rest (5). The apparition is then in the canonical position whence to abstract its shape.
No reflex can translate a chord to a canonical pitch; but pitches so project to Heschl's gyrus that octaves span equal lengths, and the information slants upward through scores of relays in vertical columns (23). Let these be tripped only by coincidence of information with a second source of excitation—say the so-called alpha activity of cortex (24), now thought to arise from thalamic circuits (25, 26, 27, 3, 28, 29) and; as this ten-per-second wave steps up and down through the cortex, its intersection with a given stream of information will move one way and the other along the axis of pitch. The output, descending vertically, then comes down in all points corresponding to these pitches in the output. When the information contains a chord of one pitch, the circuit has performed the nervous equivalent of a series of translations in pitch-conserving chord. Had we a negative feedback to stop the alpha wave when its scansion had brought the chord to a canonical pitch, the process might end here, but there is no proof that it does.
A mathematically simpler way to secure an invariant is to perform successively on any apparition the whole group of necessary transformations, sum them termwise, and divide the sums by the number of transformations (5). We need no division if the number of transformations is finite, as in brains. In figure 3, the . circuit at the right will translate a circle to the canonical position, as at the left, and sum over the translations, as in the center, where the concave block indicates the number of signals to neurons situated at each point and transmissible over a single neuron if there is a circuit to scan the sum, appearing then in time as the variable frequency of the short lines beneath. Scanning exchanges one dimension in space for time (5), which makes it possible to house the required number of neurons in our heads. As a man's name written or spoken neither looks nor sounds like the man, so these invariants need bear no resemblance to the apparition save
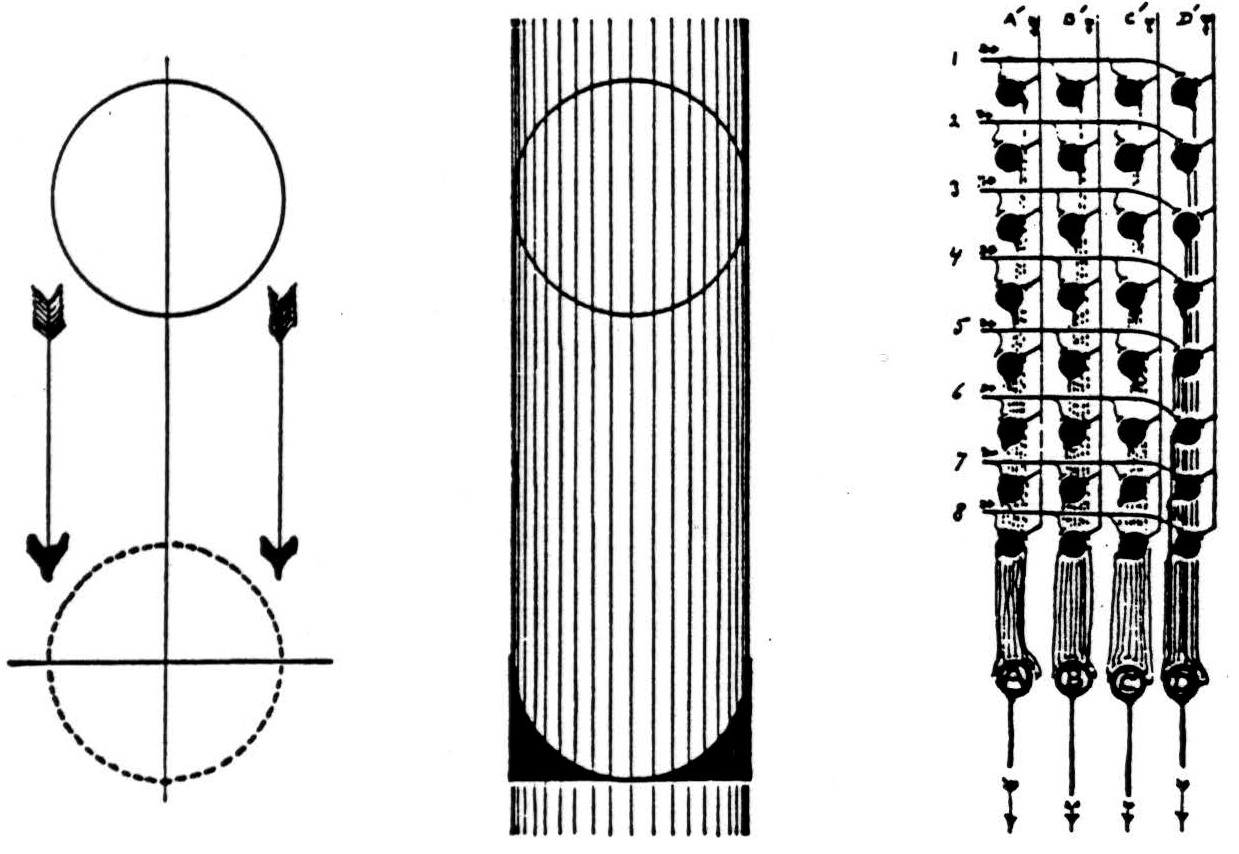
Figure 3.
a 1-1 relation according to some projective law of denotation. Hence before we look we know not what to seek in the brain.
If we did not stop the sweep but summed the vertical columns, the primary auditory cortex would relay to the secondary auditory cortex a figure corresponding to the chord and not the pitch. Now local electric stimulation in Heschl's gyrus is reported as a tone; whereas in the second auditory cortex, dreamlike experiences are induced (4). All primary receptive cortices are columnar (30), which fits this theory of ideas. So does the sweep that disappears in sleep or anesthesia, for its frequency is the greatest number of distinct perceptions per second occurring in any modality. Since a reflex (schematized in figure 4) translates visual apparitions, the primary visual cortex needs only short columns. They are imbedded in branches of its incoming fibers which then ramify widely in the horizontal plane, turning toward the surface to end on cells increasing in size and decreasing in number from below upward (31). Purely statistical considerations compel us to believe that large cells require summation from many
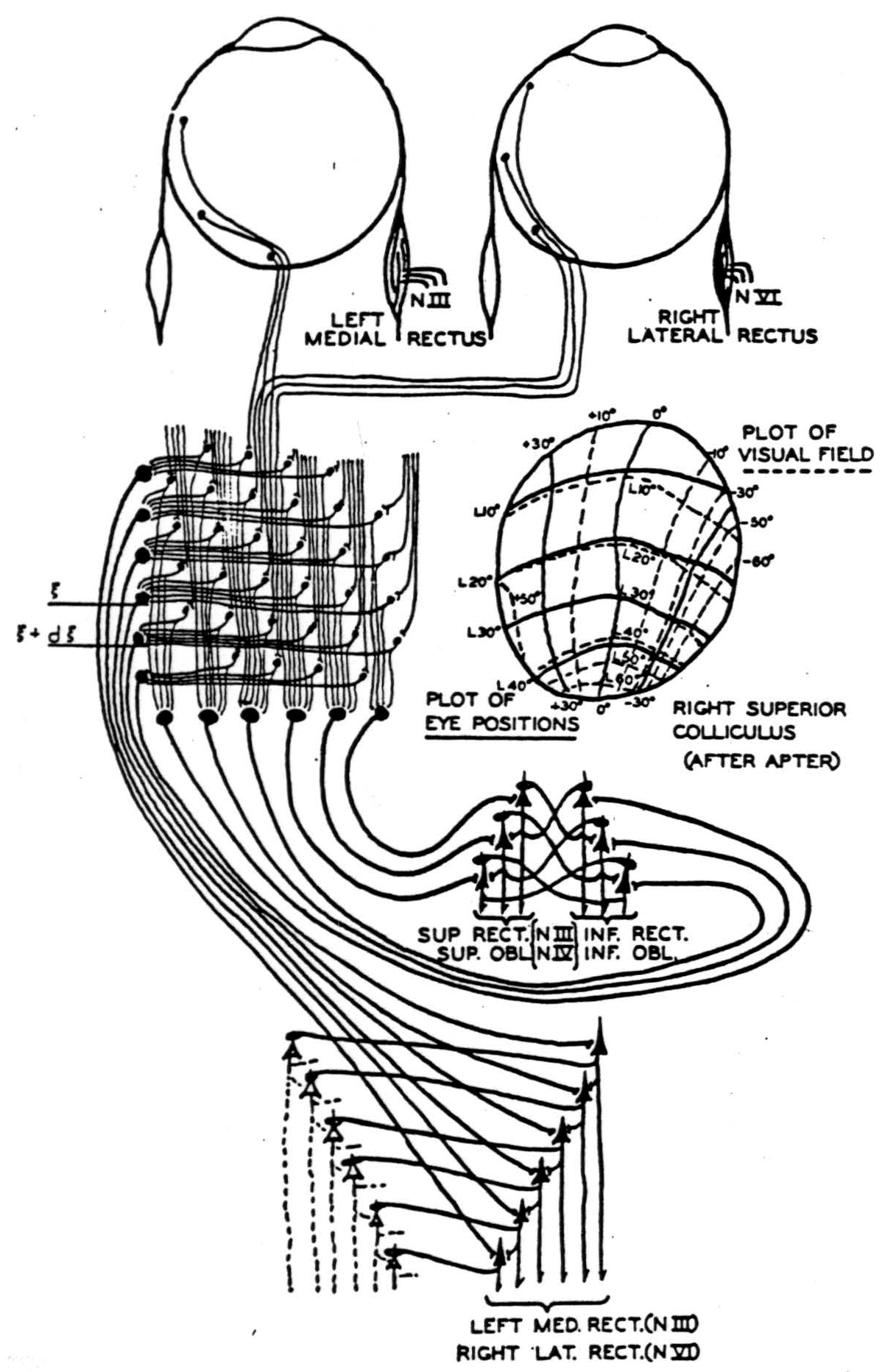
Figure 4. A simplified diagram showing occular afferente to left superior colliculus, where they are integrated antcroposteriorly and laterally and relayed to the motor nuclei of the eyes. A figure of the right auporior colliculus mapped for visual and motor response by Apter is inserted. An inhibiting synapse is indicated as a loop about the apical dendrite. The threshold of all cells is taken to be one.
This diagram is used through the courtesy of the Bulletin of Mathematical Biophysics.
endings to trip them. We would, therefore, expect the higher cells to respond to excitation over large areas, but not over small ones. A plane of excitation stepping up and down in such a cortex determines an output that runs through a group of contractions and dilatations of a figure in its input (5).
Now, the comers of an observed square tend to fill in the angles, producing an excitation like the figure on the left in figure 5. These transforms are dominated by the diagonals. A pinhead spot of strychnine anywhere in the primary visual cortex, area 17, fires cells there in unison (32). Their axons project at random to points in the secondary visual cortex (33), area 18, as I have indicated by scattering 18
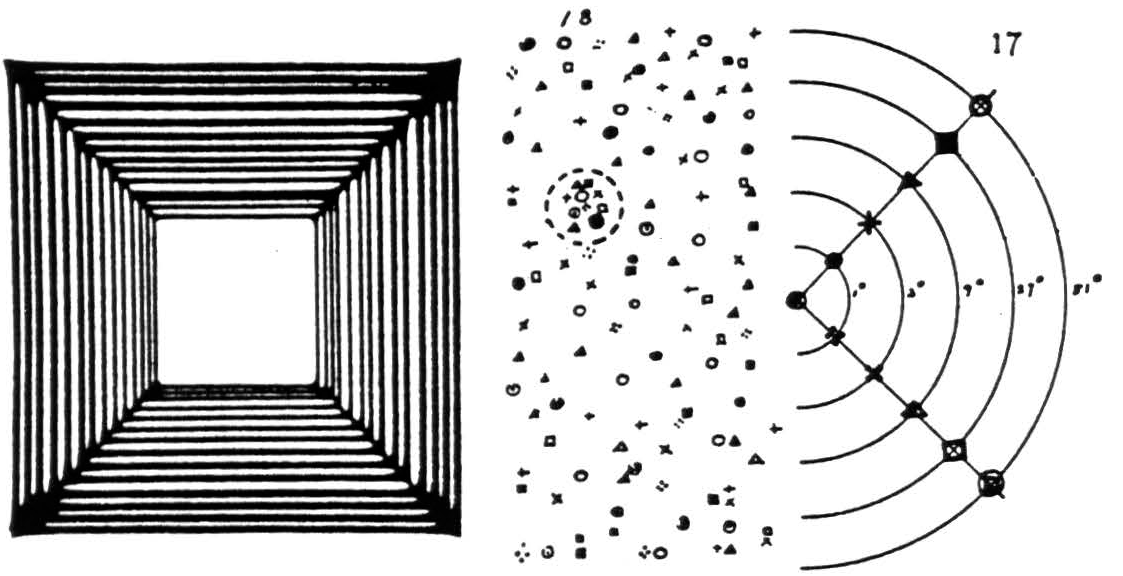
Figure 5.
replicas of each of the 11 signs placed along the diagonal lines in 17. Sheerly by chance there will arise in 18 some one small precinct, say that enclosed in the circle, to which the majority of these points project, and excitation will be maximal there. As the brain, going on coincidence, ignores or converts to inhibition (6) what falls short of summation, activity of the circled area in 18 implies the diagonals in the output of 17 and so a square regardless of size. Stimulation in area 17 yields but a vague ball of light fixed in the visual field (34); whereas, in 18, such stimulation yields a well-defined form (34) of no particular size but fixed in space, for the eyes turn thither.
The action of circuits that average over groups is little affected by perturbation of input, of threshold, or even of synapsis if connections are only to cells in proper neighborhoods (5)—a statistical order we may hope from our genes. Except possibly in the visual cortex, the horizontal connections in the gray matter need only be undisturbed for a few millimeters, for the bulk of synapsis is vertical (32, 35), and recent notable experiments on the parietal cortex showed that a 2 mm. grid of incisions through its whole thickness produced no loss of somaesthesia (36). The visual cortex may have a radial structure to be injured by such gridding; but even large holes poked through it give little or no change in the place of maximal excitation in area 18, and although scotomata can be mapped in the visual field of a man so injured, he still sees forms which for him cross the scotomata, even as they do the blind spot of a normal eye. This continuity of perceptions is not given by physical or chemical fields (37), which can only corrupt information in an organ which is a mosaic of discrete units each capable of two discrete states. Per contra, it is a consequence of the statistical nature of the process of averaging over a group of transformations which could be equally well achieved were the particular relays physically far asunder. In vision, opposite sides of the vertical line through the fovea project each to the other hemisphere with no corresponding discontinuity of perceptual properties (38).
Closed paths probably mediate our predictions. Man-made devices start a shell toward that place in the air where the plane will be when the shell arrives and explodes. In these devices, series of events in time are autocorrelated to produce invariants, like kinematic routes, most likely to be run by things that have run some part of them. Such circuits tend to reverberate in us. Optokinetic nystagmus (39), which attempts to fix gaze on things in their passage in one direction, persists when they cease to move and it attributes to them a reverse motion without change of position. This is the only known predictive circuit we may assign to a particular part of the brain and even for this there are too many equally good hypotheses. Every scientific hypothesis is a prediction. We. know only the past and little of that. Even if we are right in our superstition (40) that the previous state of the world does determine its subsequent state, any forecast we make may still go wrong—and a hypothesis forecasts the outcome of innumerable experiments. None can be proved true, any can be proved false. We must predict in order to live in a world where a false step means death. Here are errors at once inevitable and inexcusable, and the faith of any man who takes a single step is but an ignorance of ignorance concealed by universale extrapolated beyond fact.
Had we run down the fortunetelling circuits there would still be a gap in physiology which elsewhere dovetails neatly into psychology. We are ignorant of those alterations in our nets which underlie learning. The least hypothesis is that if impulses of one neuron, C, just insufficient to trip a second, R, come, concurrently with those from another, U, which can trip R, then, thereafter, C alone shall be able to trip R (41, 42). This gain in grip of C on R exemplifies the law of growth with use we now apply to other cells. Surely neurons are not immutable mummies under our microscope but are living beings, competing one with another for foot space on succeeding cells. The two axonal terminations that have been studied change with use. Myoneuronal junctions (43) and vagal endings in the ganglia in the frog's ventricle (44), on excess of stimulation, are wrecked but recover promptly and after more profound stimulation may reconstitute themselves among the useless fragments of their former state.
All protoplasm shows hysteresis (45), but that whereby anything becomes the symbol for something else—the conditional stimulus—is first found in the flat-worm (46), the lowliest beast with a truly synaptic net (46). It therefore behooves us to look to the synapse for the crucial change (43, 44). Mere change with use is not enough to substantiate the law of effect (47), which must depend on inverse feedback. Therefore, our second hypothesis is that those combinations of cells whose activity was concurrent and which were last used when we came to our goals and the activity to its end become associated. The process of learning so conceived parallels item for item the magnetizing of a bar of iron. Had we the mathematics for either, it might do for both; for both are stochastic processes in which from chaos order evolves, each step fixing to some extent what was heretofore left to chance. The theoretical difficulty is that into the relations of pairs, there enter the relations of trios and into those of trios, those of foursomes and so on to infinity (48). Such problems have not in the past proved insoluble. While I am waiting for the answer, I intend to seek the most transparent flatworms with the fewest neurons, teach them (47) and attempt to discern in the synaptic nets (46) under the microscope the difference between the scholar and the ignoramus.
Footnotes
References
Lloyd, D. P. C. In Howell's Textbook of Physiology, 15th ed., John F. Fulton, ed. Philadelphia: W. B. Saunders Co., 1946.
Lloyd, D. P. C. Facilitation and inhibition of spinal motoneurons. J. Neurophysiol., 1946, 9:421-438.
Lloyd, D. P. C. Integrative patterns of excitation and inhibition in two-neuron reflex arcs. J. Neurophysiol., 1946,9:439—444.
McCulloch, W. S. Finality and Form—Fifteenth James Arthur Lecture, New York Academy of Science, May 2, 1946, at press, Springfield, I1L: Charles Thomas.
McCulloch, W. S., and W. Pitts. How we know universale. Bull. Math. Biophyt., 1947, 9:127-147.
Brooks, C. McC., and J. C. Eccles. An electrical hypothesis of central inhibition. Nature, 1947,159:760-764.
Wittgenstein, Ludwig. Tractalus Logico-Philosophicus. London: Paul, 1922.
Wiener, N. Cybernetics. New York: John Wiley & Sons, 1948.
Hecht, Selig. Theory of visual intensity discrimination. J. Neurophysiol., 1935, 18: 767-789.
Whitehead, A. N., and B. Russell. Prindpia Mathematica. Cambridge, London, 19101913. Vol. 3.
Whitehead, A. N. Principles of Natural Knowledge. Cambridge, London, 1919.
Blake, H., W. R. Gerard, and N. Kleitman. Factors influencing brain potentials during sleep. J. Neurophysiol., 1939, 2:48-60.
Kraepun, E. Psychiatrie, 17th ed. Leipzig: J. A. Barth, 1904. Vol. 2, p. 482.
Black, H. S. Stabilized feed-back amplifier. Elec. Eng., 1934, 53:114-120.
Cannon, W. B. Organization for physiological homeostasis. Physiol. Reviews, 1929, 9: 399-431.
Dusser de Barenne, J. G., and W. S. McCulloch. Sensorimotor cortex, nucleus caudatus and thalamus opticus. J. Neurophysiol., 1938, 1:364-377.
Gellhorn, E. Effect of afferent impulses on cortical suppressor areas. J. Neurophysiol., 1947, 10:125-132.
Barker, S. H., and E. Gellhorn. Influence of suppressor areas on afferent impulses. J. Neurophysiol., 1947,10:133-138.
Maxwell, C. On Governors. Proc. Royal Soe., 1867-1868, 16:279-283.
McColl, H. Servo-Mechanisms. New York: Van Nostrand, 1945.
Rosenslueth; A., N. Wiener, and J. Bigelow. Behavior, purpose and teleology. Philosophy of Science, 1943,10:18-24.
McCulloch, W. S. A heterarchy of values determined by the topology of nervous nets. Bull, of Math. Biophyeiol., 1945, 7, 89-93.
Bailey, P., G. Von Bonin, H. W. Garel, AND W. S. McCulloch. Functional organization of temporal lobe of monkey (Macaca mulatta) and chimpanzee (Pan satyrus). J. Neurophysiol., 1943, 6:121-128.
Beroer, H. Ueber das Elektroenkephalogramm des Menschen. Arch. J. Psychiat., 1929, 87:527-570.
Bishop, G. The interpretation of cortical potentials. Cold Spring Harbor Symposia on Quan. Biol., Cold Spring Harbor, 1946,4:305-319.
Dempsey, W., and R. S. Morison. Electrical activity of thalamocortical relay system. Amer. J. Physiol., 1943,138:283-296.
Lewy, F. H., and G. D. Gammon. Influence of sensory systems on spontaneous activity of cerebral cortex. J. Neurophysiol., 1940,3:388-395.
Morison, R., and D. L. Bassett. Electrical activity of thalamus and basal ganglia in decorticate cats. J. Neurophysiol., 1945,8:309-314.
Morison, R., and E. W. Deupset. Mechanism of thalamocortical augmentation and repetition. Am. J. Physiol., 1943,138:42,297-308.
von Bonin, G., and P. Bailey. The Neocortex of Macaca Mulatto. Urbana, Ill.: University of Illinois Press, 1947.
Ramon y Cajax, S. Histologie du systéme nerveux. Paris: A. Maloine, 1909-1911.
Dusser de Barenne, J. G., and W. S. McCulloch. Functional boundaries in the sensorimotor cortex of the monkey. Proc. Soc. Exp. Biol, and Med., 1936, 35: 329-331.
Von Bonin, G., H. W. Garol, and W. S. McCulloch. The functional organization of the occipital lobe. Biol. Symposia, 1942, 7.
Penpield, W., and T. C. Erickson. Epilepsy and Cerebral Localization. Springfield, Ill.: Thomas, 1941.
Lorente de Nó, R. Chapter in John F. Fulton, Physiology of the Nervous System. New York, London, and Toronto: Oxford Press, 1943.
Sperry, R W. Cerebral regulation of motor coordination in monkeys following multiple transection of sensorimotor cortex. J. Neurophysiol., 1947, 10: 275-294.
Köhler, TV. Gestalt Psychology. New York: H. Liveright, 1929.
Helmholtz, H. L. Ferdinand von. Treatise on Physiological Optics. Translated from the 3d German ed. James P. C. Southall, ed. Rochester, New York: The Optical Society of America, 1924.
Borries, C. Reflektorischer Nystagmus. Monatsschrift für Ohrenheilkunde, 1923, LVII: 547-570.
Hume, David. Treatise on Human Nature, Being an Attempt to Introduce the Experimental Method of Reasoning into Moral Subjects. New York: E. P. Dutton & Co., 1937.
Shurrager, P. S., and Elmer J. Culler. Conditioning in the spinal dog. J. of Exp. Psychol., 1940,26:133-159.
Shurraoer, P. S., and H. C. Shurraoer Rate of learning measured at a single synapse. J. of Exp. Psychol., 1946,36:347-354.
Carey, E. J. Experimental pleomorphism of motor nerve slates as mode of functional protoplasmic movement. Anal. Rec., 1941, 81:393-413.
Fedorow, B. G. Essai de l'ltude intravitale des cellules nerveuses et des connexions interneuronales dans le systime nerveux autonome. Madrid Universidad, Laboratorio de Investigaciones Biologicas, Trabajos, 1935, 30:403-434.
Flaio, J. V. Viscosity changes in axoplasm under stimulation. J. Neurophysiol., 1947, 10: 211-221.
Moore, A. R. Individual in Simpler Form. Eugene, Ore.: University of Oregon, 1945. Chap. 108.
Thorndike, E. L. Animal Intelligence. New York: Macmillan, p. 244, 1911.
Wiener, N. On the Theory of Dense Oases. Communicated to the Macy Conference on Teleological Mechanisms, 1948. Unpublished.
Dempsey, E. W., and R. S. Morison. Production of rhythmically recurrent cortical potentials after localized thalamic stimulation. Amer. J. Physiol., 1942,135:293-300.
Hovey, H. B. Nature of apparent geotropism of young rats. Physiological Zoology, 1928, 1:550-560.
For further research:
Wordcloud: Activity, Apparition, Area, Atomic, Brain, Cells, Change, Circuits, Cortex, Dot, Ends, Events, Excitation, Eye, Feedback, Figure, Frequency, Functions, Implies, Impulses, Information, Inhibition, Light, McCulloch, Millisecond, Nature, Nets, Neurons, Neurophysiol, Number, Particular, Past, Physiology, Pitch, Probability, Psychology, Reflex, Relay, Signal, State, Step, Stimulation, Transformations, Translate, Trip, Turn, Vertical, Visual, York
Keywords: Neurons, Machine, Circuits, Brain, Cognition, Looms, Pitch, Inhibition, Impulses
Google Books: http://asclinks.live/lk5m
Google Scholar: http://asclinks.live/22bw
Jstor: http://asclinks.live/wrvr