THE STATISTICAL ORGANIZATION OF NERVOUS ACTIVITY12 [80]
W.S. McCulloch and W. Pitts
Introduction
This is not a review of neurophysiology but a synopsis of some theories which may lead to an understanding of the mental aspects of nervous activity, namely ideas and purposes. The highway to ideas lies through statistical conceptions from their logical foundation in Boolean algebra through modem methods of constructing invariants by averaging over groups of transformations. Purposive behavior depends upon how output affects input which, in turn, depends upon a nervous system whose organization can be treated statistically. This is instanced in one reflex. Known details of other mechanisms are in current publications. The theory is extremely atomistic. The ultimate units of nervous activity are impulses which, being all-or-none signals, submit to the Boolean algebra of propositions and hence to statistical treatment. A field-theory does not now exist and may never cope with the inherent complexities. It has been shown to be unnecessary.
Figure 1 shows a neuron, and labels the dendrites, cell-body and axon. Proper irritation of the cell starts off a signal, a ring of negative voltage, which then travels from the body along the axon and its branches at a speed between one foot and three hundred feet per second, depending upon the thickness of the axon. The thicker axons are also longer, so that the total time of transit is more nearly the same from the beginning to end of any axon than if all were of one diameter. We ahall treat this time as if it were constant, and therefore negligible. The end of an axon is either in a muscle or gland, or else forms a small knob on another neuron, as in Figure 2. These knobs are called synapses. Signals arriving at synapses irritate the recipient neuron locally for about two-tenths of a millisecond. If signals arrive within that time on enough of its synapses, they combine to start off a signal half a millisecond later along the axon of the recipient neuron. The amount of irritation required for
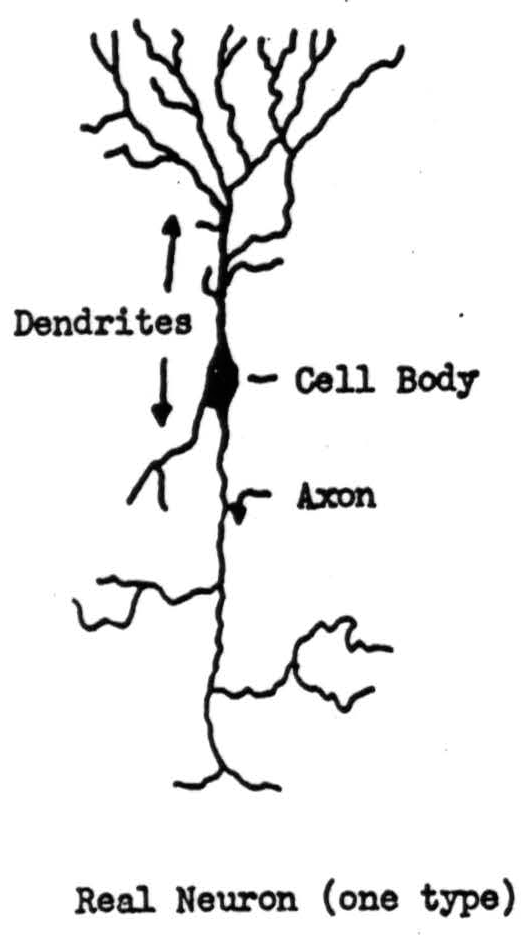
Figure 1.
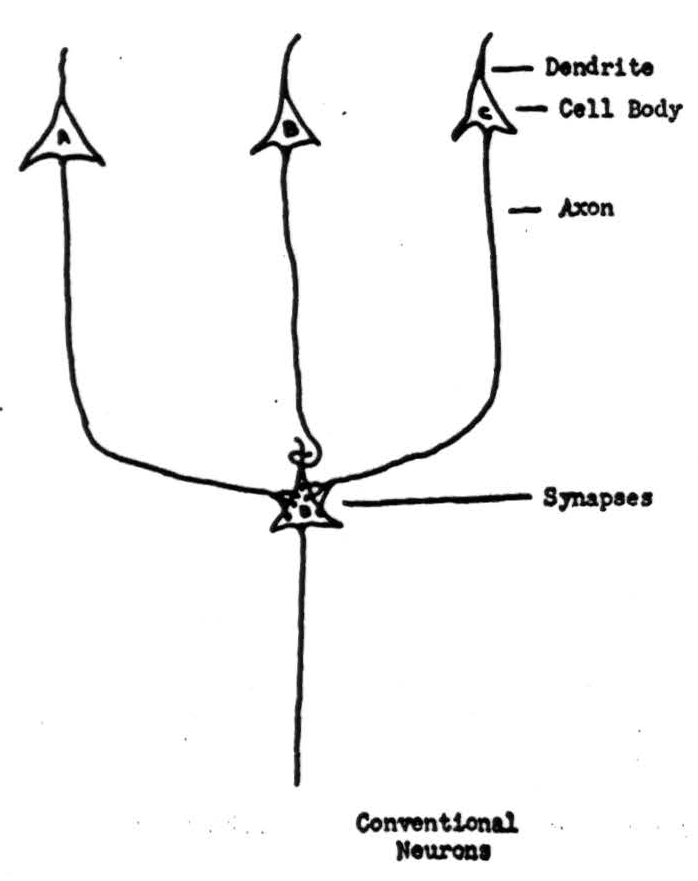
Figure 2.
This is called the threshold of the neuron and the delay the synaptic delay. After transmitting one signal, a neuron will not transmit another for about eight-tenths of a millisecond: it is said to be refractory. It is obvious from this that no two successive signals along the same axon can combine their irritation at the terminal synapse. Although the anatomy is not known, impulses arriving somewhere in the vicinity of a neuron, either directly or by way of sub-threshold irritation of intermediary neurons, do prevent the neuron in question from responding to otherwise adequate irritation. We draw such an inhibitory ending as a loop around a dendrite, as in Figure 2. Neurons are unlike ordinary electric circuits in that the energy sustaining the signal is always sup• plied locally; that is why its final size is not affected by events at its origin or along its course. Neurons have other properties which we shall ignore in the present sketch.
Let time flow equally in measured lapses, say a millisecond apiece, and number them beginning with anyone that is convenient. A given neuron cannot transmit two signals in a single lapse: it must have either one on it or none. For every such lapse, there is, therefore one proposition, say SA(t) for neuron A, such that knowledge of its truth or falsity describes the neuron completely—namely, SA(t) asserts that there is a signal on A at L Further, since neurone influence one another only by signals, all the significant relations within a nervous net can be expressed as propositional relations which only involve truth-values. This is to say that nervous activity can be described in the calculus of propositions as follows. If, for two propositions p and q, we use the notations:
∼ p = 'p is false,' ‘not p’
p + q = ‘either p or q or both’
p · q — ‘both p and q’
p ⊃ q = ‘if p then q', ‘p implies q’
p = q = ‘p if and only if q',
then possible relations between the actions of neurons in Figure 2 will include the cases:
Simultaneous summation from both A and C is necessary to to excite D:
SD(t+ 1) ≡ SA(t)-Sc(t).
Either A or C is alone capable of exciting D:
SD(t + 1) ≡ SA(t) + Sc(t).
A can excite D unless B inhibits it:
SD(t + 1) ≡ SA(t)-∼SB(t).
In the whole nervous net, we shall have an equivalence of this kind defining the conditions of excitation for each neuron in the net. Provided the net is free of circular paths—that is, if it is never possible to follow down the axon of a neuron and its successors in such a way as to return to the starting point—then these equivalences may be substituted into one another so as to obtain, for each output-neuron, a set of necessary and sufficient conditions of excitation, in the form prescribed by this calculus, in terms of the signals coming into the system as input from senseorgans. If we are allowed extra delay between input and output, we can construct a net to make the output any desired logical function of the input, provided only it satisfy the condition that it is false when all its atomic components asserting the occurrence of signals in the input are false. For if no signals ever enter the net, none can emerge. If spontaneously active neurons are admitted, this restriction also vanishes.
If neurons successively excite one another in a circle, a signal, once started can circulate through the net indefinitely. Among other things, such circuits introduce the universal and existential operators of logic applied to time past. They constitute a memory of a kind, whereby, in principle, signals delivered once to a net may cause it to behave differently to certain inputs forever after. The actual durability of learning requires more stable devices than this, amounting to a change in the connections of the net: but this may not come formally to anything very different. To make marks and read them later also brings consequences formally similar to circulating activity in the net.
Besides these microscopic properties, the ten billion neurons in the brain show regularities in the large which are properly statistical, and are necessary for a nervous system to survive and reproduce.
One kind extracts the important universale out of the excessive particularity of their exemplars. An animal must recognize visible objects irrespective of his distance from them and his perspective—that is, independent of their absolute size or position in the visual field. The latter invariance he secures by a reflex which snaps the eyes to the “center of brightness” and the image therewith to a standard place. This is one general kind of mechanism. A second secures the size-invariance of shapes: the nervous system may actually form all the possible magnifications and constrictions of the image, either simultaneously at different places or successively at one place, calculate an important parameter for each size, and add them. Such a sum would have been the same, by definition, if we had started with the same shape in a different size. Enough invariant sums of this kind may be computed to enable the system to recognize the form as well as it needs to. Since, in a finite net, the number of such transformations is finite, these sums are really averages over groups of transformations.3
‘Mechanisms differ from one another in the oaloulation of parameters to be averaged. Thus, in effect, the reflex that oenters gate on objects to be recognised, by moving the eye so rapidly as to flush the visual cortex with “ons” and “offs”, assigns there the value zero to all translations except the last.
Another statistical principle of organization occurs wherever the nervous system, built on all-or-none principles, has to deal with the important variables in the physical world that are continuous along one or several dimensions. Light varies continuously in intensity, hue, and shade; sound, in loudness and pitch; and so on. The nervous system represents these magnitudes as averages of many kinds. It averages over time when a sense-receptor emits a series of impulses whose frequency measures the intensity of the continuous variable stimulating it or when a muscle fiber in tetanus adds increments of tension evoked bysignals along the innervating axon during some time past. It likewise averages in space when a higher grade of a sensory variable stimulates more receptors or more motor axons excite more fibers in a muscle. This is one reason for the enormous reduplication of parallel paths in the nervous system. The result of all this averaging is a very fair approximation to a continuous dynamical control-system for gaging the application of physical force to move matter in the light of continuous information about the consequences.
These matters are well illustrated in the simple case of the stretchreflex. With some simplification, the mechanism is diagrammed in Figure 3. Receptors in the muscle send signals into the spinal cord at a frequency ρ which is some monotonic function f(L) of the length of the muscle. These signals are reduplicated in branches of the sensory axons carrying them to converge on the motor cells of the ventral horn, which innervate the same muscle. The motor neuron will transmit a signal whenever the number of afferent signals coinciding on it within a short interval exceeds the threshold h. We shall take this interval as the unit of time. If afferent impulses are statistically independent and asynchronous, the probability-distribution of the total number arriving per unit time will tend either to the Gaussian or the Poisson distribution, depending upon the magnitude of p. In the former case, if N be the average number of different axons afferent to one motor neuron, the mean will be Nρ and the variance Nρ( 1 − ρ) so that the average number of signals per unit time delivered to the muscle along a motor axon will be
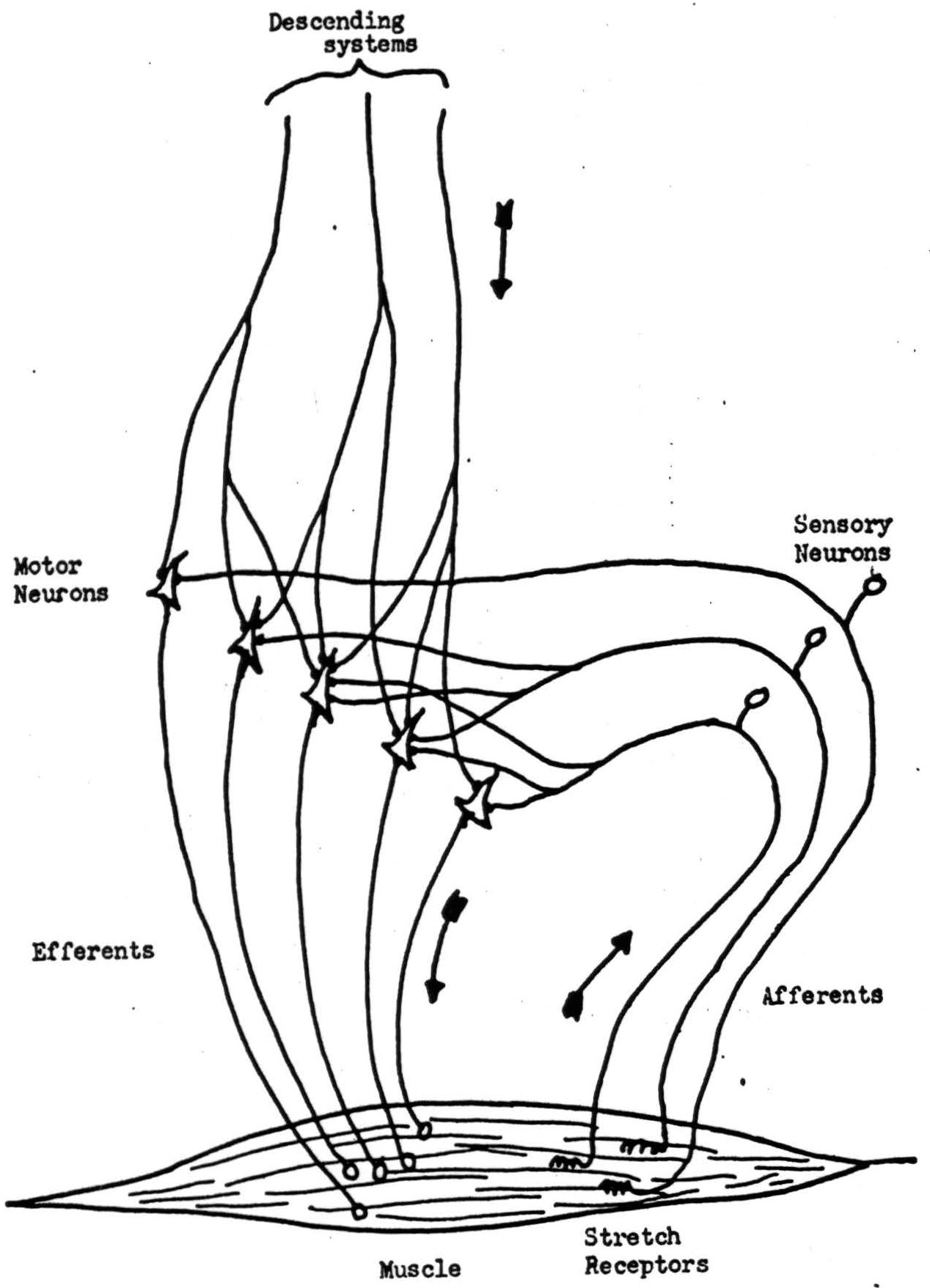
Figure 3.
in which h′ = h/N, the relative threshold. E(ρ) is sigmoid, monotonic, and varies from zero to unity as p does, provided that h′ < 1.4 We see that the inflection point of E(ρ) is reached as ρ reaches the relative threshold h′and that its slope at that point is proportional to the square root of N. This mean frequency E(ρ), delivered over the axons innervating the muscle, will develop a tension given by a certain monotonic function T = T(E), which then tends to reduce the length of the muscle. This familiar process, whereby a change in the output causes a change of opposite sign in the input, sets equilibrium length L and a tension T which just holds that length against the external load. It also returns the muscle to that length if it be perturbed from without in any way.
It is evident that the equilibrium length sought by the reflex under given circumstances can be varied at will by controlling the value of the central threshold h′. Formally, this is exactly the effect wrought by additional signals descending from higher nervous structures to intervene in the stretch-reflex arc. The engineer would say that the signals from higher structures control the gain around the loop of the stretch-reflex. Quite generally, this is the plan of sub- and super-ordination prevailing in the nervous system. No higher structure alone can move muscles: it can only control the “central amplification” of the elementary spinal reflex arc. In monkeys, to cut off all the afferents from a limb acutely paralyzes it as completely as if the motor nerve had been severed.
Three or four principal circuits send parallel descending tracts to control the spinal cord in this way. Some of them proceed from their own sensory afferents and, in turn have their own gains controlled by super-ordinate systems. Thus the labyrinths inform the vestibulospinal circuit which direction is down, whereupon it amplifies the stretchreflex in the anti-gravity muscles accordingly. Similar circuits control the velocity of movement, to keep it smooth and in constant relation to moving physical objects. Others support the body at even temperature, the blood pressure constant, and the respiration sufficient to hold the carbon dioxide and oxygen tensions at proper values. Many of them are regularly periodic, like those of walking, breathing, and sleeping.
There are circuits that pass from the central nervous system through effectors into the world about us to procure the necessities of life: and, of them, some, making use of symbols, keep us adjusted to the complication of society. When two are incompatible, choice is insured either by one inhibiting the other or by a requirement of summation from the rejected to the preferred. Since, of three such circuits, the first may dominate the second, the second the third, and the third the first, values need have no common measure. When these circuits are built into us by the usual processes of growth, they operate so automatically that we are scarcely aware of them. Experience of choice usually arises at the moment we are forced to make a novel decision.
At present, we do not know how our nets are changed by such decision. We try many things and finally succeed; the successful mode of action most commonly becomes the preferred: but whether this is due to growth of neurons or changes in threshold is obscure. Heredity cannot fix the thresholds and connections of so many neurons. It can only lay down the general plan and leave particulars to chance. Experience brings order into this chaos and in doing so, gives us a memory, unlike a written record. It is better conceived as the establishment of a connection, which, once made, works henceforth so that the new is always built upon the old. This gradual ordering of the nervous system is like permanent magnetization in an originally unmagnetic bar of steel. Apart from learning, a mathematical account of nervous systems whose connections are random in detail is part of the complex and incomplete realm of statistical mechanics that deals with change of state. Even so, numerous calculations of quantities measured in experimental electrophysiology have been made, and there is reason to expect more in the near future.
We can summarize our conclusions as follows:
The actions of neurons and their mutual relations can be described by the calculus of propositions subscripted for time.
The nervous system as a whole is ordered and operated on statistical principles. Thereby it adjusts the all-or-none laws governing its elements to a physical world of continuous variation.
It detects universals.
It conserves its own level of activity, the condition of the body it inhabits, and its relation to the physical world by activity in closed paths such that a change in its output causes a change of opposite sign in its input.
It chooses between ends.
It alters its structure by experience.
Finally, the mathematical treatment of its activity presents numerous problems in the theory of probability and stochastic processes.
Bibliography
Adrian, E. D., “General Principles of Nervous Activity”, Brain, 70, 1, 1-18 (1947).
Bell, Sir Charles, “On the Nervous Circle, etc.”, Read before the Royal Society, February 16, 1826.
Boole, G., An Investigation of the Laws of Thought. 1854, London. Reprinted: The Laws of Thought, Open Court Publishing Co., Chicago and London, 1940.
Brooks, C. Me., and Eccles, J. C., “Electrical Hypothesis of Central Inhibition”, Nature, 159, 760-764 (1947).
Lloyd, D., “Activity in neurons of the bulbospinal correlation system”, Journal of Neurophysiology, 4, 1, 113-137 (1941). .
Lloyd, D., “The spinal mechanism of the pyramidal system in cats”, Journal of Neurophysiology, 4, 7, 525-547 (1941).
Lloyd, D., “Facilitation and inhibition of spinal motoneurons”, Journal of Neurophysiology, 9, 6, 421-438 (1946).
Lloyd, D., “Integrative pattern of excitation in two-neuron reflex arcs”, Journal of Neurophysiology, 9, 6, 439-445 (1946).
Magendie, T., “Mfimoire sur Quelques Dicouvertes Ricentes Relatives aux Factions du Systeme Nerveux”. Lu a la seance publique de l'Acadamie des Sciences, Paris, 1823.
Maxwell, Clark, “On Governors”, Proceedings of the Royal Society, 100, (1868).
McCulloch, W. S., and Pitts, W., “A logical calculus of the ideas immanent in nervous activity”, Bulletin of Mathematical Biophysics, 7, 89-93 (1943).
McCulloch, W. S., “The functional organization of the cerebral cortex”, Physiological Reviews, 4, 3, 390-407 (1944).
McCulloch, W. S., “A heterarchy of values determined by the topology of nervous nets”, Bulletin of Mathematical Biophysics, 7, 89-93 (1945).
McCulloch, W. 8., “Finality and form in nervous activity”, Fifteenth Annual James Arthur Lecture at the American Museum of Natural History, New York, May 1946.
McCulloch, W. S., “Machines that know and want”, American Psychological Society, Detroit, 1947.
Pitts, W. and McCulloch, W. S., “How we know universale”, Bulletin of Mathematical Biophysics, 9, 127-147 (1947).
McCulloch, W. S., “Modes of functional organization of the cerebral cortex”, Federation Proceedings of the American Societies far Experimental Biology, 6, 2 (1947).
McCulloch, W. S., and Lettvin, J. Y., “Somatic functions of the central nervous system”, Annual Review of Physiology. In Press.
Lorente de Nó, R., Journal für Psychologie und Neurologie, 45: H.6, 381 (1934).
Lorente de Nó, R., Journal für Psychologie und Neurologie, 45: H.2 u.3, 113 (1934).
Weyl, H., The Theory of Groups and Quantum Mechanics, Methuen &; Co., Ltd., London, 1931.