A STATISTICAL CONSEQUENCE OF THE LOGICAL CALCULUS OF NERVOUS NETS¹ [52]

H.D. Landahl, W.S. McCulloch and W. Pitts

A formal method is derived for converting logical relations among the actions of neurons in a net into statistical relations among the frequencies of their impulses.

Consider the neuron c_n upon which c₁, …, c_p have excitatory, and c_p+1, …, c_p+q inhibitory synapses. Let δ be the period of latent addition, so that c_n is excited at the time t if and only if the number of impulses along c₁, …, c_p which have concurred within an interval of duration δ about t−1 exceeds θ_n and none has occurred within δ along any of c_p+1, …, c_p+q. Suppose that the sequences of impulses along c₁, …, c_p are statistically independent, and let ν_i be the mean frequency of impulses along c_i. Then the mean proportion of time that exactly r excitatory impulses arrive upon c_n within an interval of duration δ is given by

\mathop \Sigma \limits_{i{{\kern 1pt} _{r = 1{\kern 1pt} r - 1}} + 1}^{i{{\kern 1pt} _r} = p} ...\mathop \Sigma \limits_{i{{\kern 1pt} _2} = i1 + 1}^{i{{\kern 1pt} _2} = p} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \mathop \Sigma \limits_{i{{\kern 1pt} _1} = 1}^{i{{\kern 1pt} _1} = p} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \mathop \Pi \limits_{j = 1}^{j = r} {\mkern 1mu} {\mkern 1mu} {\delta ^r}{v_{{i_j}}}.{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (1)

Consequently, the mean proportion of time Κ that the number of impulses concurring upon c_n within δ exceeds θ_n is obtained by summing (1) from r = θ_n to r = p. The intervals of duration δ within which impulses from any of c_p+1, …, c_p+q occur are intervals when c_n is inexcitable. The mean proportion of time when this is not the case is given by

$\;\mathop {II}\limits_{k = p + 1}^{k = p + q} \,\,(1 - \delta \;{v_k}).\,\,\,\,\,\,\,\,(2)$

The frequency ν_n is then the product of (2) by Λ, or

{v_n} = {\delta ^{ - 1}}\mathop \Pi \limits_{k = p + 1}^{k = p + q} (1 - \delta \,{v_k})\mathop \Sigma \limits_{r = {\theta _n}}^{r = p} \,\,\mathop \Sigma \limits_{{i_{r = 1\,r - 1}} + 1}^{{i_r} = p} ...\mathop \Sigma \limits_{i{\,_{2 = i + 1}}}^{i{\,_2} = p} \,\,\,\,\mathop \Sigma \limits_{i{\,_1} = 1}^{i{\,_1} = p} \,\,\,\mathop \Pi \limits_{j = 1}^{j = r} \,\,{\delta ^r}{v_{{i_j}}}.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)

If we compare equation (3) with expression (1) of the preceding paper(1), whose notation we shall use, and apply a straightforward inductive argument, we obtain the following

Theorem.

Let 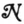be a net of order zero, or, more generally, one for which

N_i(z) = S_i [i = 1, … , s]

is a solution wherein the S_i fulfill the conditions of Theorem X of the preceding paper. Let ν_j be the mean frequency of impulses in c_j, and let the expression A_i be generated out of S_i by the following rules:

Replace each N of Sᵢ by ‘δ ν’ with the same subscript.
Replace every v by ‘ + ’, every · by ‘ × ’ and every ∾ by ‘1—’.
Replace the operators (z_i) and (Ez_i $\mathop {II}\limits_{{z^1} = 0}^{{z^2} = {z^1}}$ $\mathop \Sigma \limits_{{z^1} = 0}^{{z^2} = {z^1}}$ wherever they occur.
Replace every occurrence of a predicate C_mn by a symbol for the function f_mn (t) which is defined for all natural numbers t as unity when t = m (mod n), and otherwise zero.

Then the frequencies of impulses in the c_i are given in terms of those of the peripheral afferents by the equations

$\delta {\rm{ }}{\nu _i} = {A_i}[i = 1, \; \ldots ,\; s].{\rm{ (4)}}$

The correspondence expressed by this theorem is exactly that of Boole between the algebra of logic and that of probability. It connects the logical calculus of the preceding paper with previous treatments of the activity of nervous nets in mathematical biophysics and with quantitatively measurable psychological phenomena. For these phenomena we can construct hypothetical nets by the powerful methods of the preceding calculus. The theorem then enables us to determine specific predictions from the quantitative characters of the stimulus to those of the response. These predictions can be compared with observations and, if necessary, the nets be altered until the consequent predictions are verified.

But this procedure leads to error whenever the assumptions leading to equation (3) are not fulfilled. This will be the case if the frequencies are too great, but the limit is many times the maximum observed. When the frequencies are too small, the statistical treatment, though valid, is of little help, but we may here conveniently use the logical calculus directly. The same obtains in microscopic physiological analysis. The most important exceptions are those which arise from physiological factors that synchronize activities and thus restrict the domain of the validity of the assumption of statistical independences required in the derivation of equation (3).

Footnote

Literature

McCulloch, Warren S. and Walter Pitts. 1943. “A Logical Calculus of the Ideas Immanent in Nervous Activity.” Bull. Math. Biophysics, 5, 115-133.

For further research:

Wordcloud: Activity, Along, Biophysics, Calculus, Consequent, Delta, Duration, Equation, Excitatory, Expression, Following, Frequencies, Fulfill, Given, Impulses, Interval, Kern, Limits, Logical, Mathop, Mkern, Mu, Nervous, Nets, Number, Observed, Obtain, Occur, Paper, Phenomena, Pi, Pitts, Preceding, Predictions, Proportion, Quantitative, Relations, Replace, Sigma, Statistical, Theorem, Zero

Keywords: Impulses, Relations, Science, Theorem, Nets, Neurons, Method

Google Books: http://asclinks.live/0pdr

Google Scholar: http://asclinks.live/leqn

Jstor: http://asclinks.live/9ayp

1 Reprinted from Bulletin of Mathematical Biophysics, 5 : 135-137, 1943. ↩

A STATISTICAL CONSEQUENCE OF THE LOGICAL CALCULUS OF NERVOUS NETS1 [52]

Theorem.

Footnote

Literature

A STATISTICAL CONSEQUENCE OF THE LOGICAL CALCULUS OF NERVOUS NETS¹ [52]