A LOGICAL CALCULUS OF THE IDEAS IMMANENT IN NERVOUS ACTIVITY[^*] [51]

W.S. McCulloch and W. Pitts

Abstract

Because of the “all-or-none” character of nervous activity, neural events and the relations among them can be treated by means of propositional logic. It is found that the behavior of every net can be described in these terms, with the addition of more complicated logical means for nets containing circles; and that for any logical expression satisfying certain conditions, one can find a net behaving in the fashion it describes. It is shown that many particular choices among possible neurophysiological assumptions are equivalent, in the sense that for every net behaving under one assumption, there exists another net which behaves under the other and gives the same results, although perhaps not in the same time. Various applications of the calculus are discussed.

Introduction

Theoretical neurophysiology rests on certain cardinal assumptions. The nervous system is a net of neurons, each having a soma and an axon. Their adjunctions, or synapses, are always between the axon of one neuron and the soma of another. At any instant a neuron has some threshold, which excitation must exceed to initiate an impulse. This, except for the fact and the time of its occurrence, is determined by the neuron, not by the excitation. From the point of excitation the impulse is propagated to all parts of the neuron. The velocity along the axon varies directly with its diameter, from less than one meter per second in thin axons, which are usually short, to more than 150 meters per second in thick axons, which are usually long. The time for axonal conduction is consequently of little importance in determining the time of arrival of impulses at points unequally remote from the same source. Excitation across synapses occurs predominantly from axonal terminations to somata. It is still a moot point whether this depends upon the irreciprocity of individual synapses or merely upon prevalent anatomical configurations. To suppose the latter requires no hypothesis ad hoc and explains known exceptions, but any assumption as to cause is compatible with the calculus to come. No case is known in which excitation through a single synapse has elicited a nervous impulse in any neuron, whereas any neuron may be excited by impulses arriving at a sufficient number of neighboring synapses within the period of latent addition, which lasts less than one-quarter of a millisecond. Observed temporal summation of impulses at greater intervals is impossible for single neurons and empirically depends upon structural properties of the net. Between the arrival of impulses upon a neuron and its own propagated impulse, there is a synaptic delay of more than half a millisecond. During the first part of the nervous impulse, the neuron is absolutely refractory to any stimulation. Thereafter its excitability returns rapidly, in some cases reaching a value above normal, from which it sinks again to a subnormal value, whence it returns slowly to normal. Frequent activity augments this subnormality. Such specificity as is possessed by nervous impulses depends solely upon their time and place and not on any other specificity of nervous energies. Of late only inhibition has been seriously adduced to contravene this thesis. Inhibition is the termination or prevention of the activity of one group of neurons by concurrent or antecedent activity of a second group. Until recently, this could be explained on the supposition that previous activity of neurons of the second group might so raise the thresholds of internuncial neurons that they could no longer be excited by neurons of the first group. In contrast, the impulses of the first group must sum with the impulses of these internuncials to excite the now inhibited neurons. Today, some inhibitions have been shown to consume less than one millisecond. This excludes internuncials and requires synapses through which impulses inhibit that neuron which is being stimulated by impulses through other synapses. As yet experiment has not shown whether the refractoriness is relative or absolute. We will assume the latter and demonstrate that the difference is immaterial to our argument. Either variety of refractoriness can be accounted for in either of two ways. The “inhibitory synapse” may be of such a kind as to produce a substance which raises the threshold of the neuron, or it may be so placed that the local disturbance produced by its excitation opposes the alteration induced by the otherwise excitatory synapses. Inasmuch as position is already known to have such effects in the case of electrical stimulation, the first hypothesis is to be excluded unless and until it be substantiated, for the second involves no new hypothesis. We have, then, two explanations of inhibition based on the same general premises, differing only in the assumed nervous nets and, consequently, in the time required for inhibition. Hereafter we shall refer to such nervous nets as equivalent in the extended sense. Since we are concerned with properties of nets which are invariant under equivalence, we may make the physical assumptions which are most convenient for the calculus.

Many years ago, one of us, by considerations impertinent to this argument, was led to conceive of the response of any neuron as factually equivalent to a proposition which proposed its adequate stimulus. He, therefore, attempted to record the behavior of complicated nets in the notation of the symbolic logic of propositions. The “all-or-none” law of nervous activity is sufficient to ensure that the activity of any neuron may be represented as a proposition. Physiological relations existing among nervous activities correspond, of course, to relations among the propositions, and the utility of the representation depends upon the identity of these relations with those of the logic of propositions. To each reaction of any neuron, there is a corresponding assertion of a simple proposition. This, in turn, implies either some other simple proposition or the disjunction or the conjunction, with or without negation, of similar propositions, according to the configuration of the synapses upon and the threshold of the neuron in question. Two difficulties appeared. The first concerns facilitation and extinction, in which antecedent activity temporarily alters responsiveness to subsequent stimulation of one and the same part of the net. The second concerns learning, in which activities concurrent at some previous time have altered the net permanently so that a stimulus which would previously have been inadequate is now adequate. But for nets undergoing both alterations, we can substitute equivalent fictitious nets composed of neurons whose connections and thresholds are unaltered. But one point must be made clear: neither of us conceives the formal equivalence to be a factual explanation. Per contra!—we regard facilitation and extinction as dependent upon continuous changes in threshold related to electrical and chemical variables, such as after-potentials and ionic concentrations, and learning as an enduring change which can survive sleep, anesthesia, convulsions, and coma. The importance of the formal equivalence lies in this: that the alterations actually underlying facilitation, extinction, and learning in no way affect the conclusions which follow from the formal treatment of the activity of nervous nets, and the relations of the corresponding propositions remain those of the logic of propositions.

The nervous system contains many circular paths, whose activity so regenerates the excitation of any participant neuron that reference to time past becomes indefinite. However, it still implies that afferent activity has realized one of a certain class of configurations over time. Precise specification of these implications by means of recursive functions, and determination of those that can be embodied in the activity of nervous nets, completes the theory.

The Theory: Nets Without Circles

We shall make the following physical assumptions for our calculus.

The activity of the neuron is an “all-or-none” process.
A certain fixed number of synapses must be excited within the period of latent addition in order to excite a neuron at any time, and this number is independent of previous activity and position on the neuron.
The only significant delay within the nervous system is synaptic delay.
The activity of any inhibitory synapse absolutely prevents excitation of the neuron at that time.
The structure of the net does not change with time.

To present the theory, the most appropriate symbolism is that of Language II of R. Carnap (1), augmented with various notations drawn from B. Russell and A. N. Whitehead (2), including the Principia conventions for dots. Typographical necessity, however, will compel us to use the upright ‘E’ for the existential operator instead of the inverted and an arrow (‘→’) for implication instead of the horseshoe. We shall also use the Carnap syntactical notations but print them in boldface rather than German type, and we shall introduce a functor S, whose value for a property P is the property which holds of a number when P holds of its predecessor; it is defined by ‘S (P) (t). P(Kx) . t = x)’; the brackets around its argument will often be omitted, in which case this is understood to be the nearest predicate-expression [Pr] on the right. Moreover, we shall write S²Pr for S (S(Pr)), etc.

The neurons of a given net 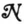IF1 may be assigned designations ‘c₁’, ‘c₂’, ..., ‘c_n.’ This done, we shall denote the property of a number that a neuron c_i fires at a time which is that number of synaptic delays from the origin of time, by ‘N’ with the numeral i as subscript, so that N_i(t)asserts that c_i fires at the time t. N_i is called the action of C_i. We shall sometimes regard the subscripted numeral of ‘N’ as if it belonged to the object language and were in a place for a functoral argument, so that it might be replaced by a number-variable [z] and quantified ; this enables us to abbreviate long but finite disjunctions and conjunctions by the use of an operator. We shall employ this locution quite generally for sequences of Pr; it may be secured formally by an obvious disjunctive definition. The predicates ‘N₁’, ‘N₂’, ... , comprise the syntactical class .’

Let us define the peripheral afferents of 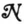IF1 as the neurons of 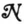IF1 with no axons synapsing upon them. Let N₁, ... , N_p denote the actions of such neurons and N_p+1, N_p+2, ..., N_n those of the rest. Then a solution of 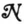IF1 will be a class of sentences of the form S_i: N_p+1 (z₁). Pr_i (N₁, N₂, ..., N_p, z₁), where Pr_i contains no free variable save z₁ and no descriptive symbols save the N in the argument [Arg], and possibly some constant sentences [sa]; and such that each S_i is true of 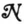IF1 . Conversely, given a Pr₁ (¹p¹ ₁, ¹p¹ ₂, ..., ¹p¹_p, z₁, s), containing no free variable save those in its Arg, we shall say that it is realizable in the narrow sense if there exists a net 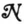IF1 and a series of N_i in it such that N₁(z₁) .≡. Pr₁(N₁, N₂, ... , z₁, sa₁) is true of it, where sa₁ has the form N(0). We shall call it realizable in the extended sense, or simply realizable if for some n Sⁿ(Pr₁) (p₁, ..., p_p, z₁, s) is realizable in the above sense. c_pi is here the realizing neuron. We shall say of two laws of nervous excitation which are such that every S which is realizable in either sense upon one supposition is also realizable, perhaps by a different net, upon the other, that they are equivalent assumptions, in that sense.

The following theorems about realizability all refer to the extended sense. In some cases, sharper theorems about narrow realizability can be obtained. Still, in addition to greater complication in statement this were of little practical value since our present neurophysiological knowledge determines the law of excitation only to extended equivalence, and the more precise theorems differ according to which possible assumption we make. Our less precise theorems, however, are invariant under equivalence and are still sufficient for all purposes in which the exact time for impulses to pass through the whole net is not crucial.

Our central problems may now be stated exactly: first, to find an effective method of obtaining a set of computable S constituting a solution of any given net, and second, to characterize the class of realizable S in an effective fashion. Materially stated, the problems are to calculate the behavior of any net and to find a net which will behave in a specified way when such a net exists.

A net will be called cyclic if it contains a circle: i.e., if there exists a chain c_i, c_i+1, ..., c_p of neurons on it, each member of the chain synapsing upon the next, with the same beginning and end. If a set of its neurons c₁, c₂, ..., c_p is such that its removal from 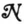IF1 leaves it without circles, and no smaller class of neurons has this property, the set is called a cyclic set, and its cardinality is the order 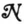IF1 . In an important sense, as we shall see, the order of a net is an index of the complexity of its behavior. In particular, nets of zero order have especially simple properties ; we shall discuss them first.

Let us define a temporal propositional expression (a TPE), designating a temporal propositional function (TPF) by the following recursion:

A ¹p¹[z₁] is a TPE, where p₁ is a predicate variable.
If S₁ and S₂ are TPE containing the same free individual variable, so are SS₁, S₁vS₂, S₁.S₂ and S_i. ∾ S₂.
Nothing else is a TPE.

Theorem I.

Every net of order 0 can be solved in terms of temporal propositional expressions.

Let c_i be any neuron of 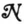IF1 with a threshold θ_i > 0, and let c_i1, C_i2, ..., c_ip have respectively n_i1, n_i2, ..., n_ip excitatory synapses upon it. Let c_j1, c_j2, ..., c_jq have inhibitory synapses upon it. Let be κ_i the set of the subclasses of {n_i1, n_i2, ..., n_ip} such that the sum of their members exceeds θ_i. We shall then be able to write, in accordance with the assumptions mentioned above,

N_{i} (Z_{1}) . \equiv . S {\prod_{m \subset 1}^{q} \infty N_{j m} (z_{1}) . \underset{α ε κ_{i}}{Σ} \underset{s ε α}{Π} N_{i n} (z_{1})} (1)

where the ‘Σ’ and ‘Π’ are syntactical symbols for disjunctions and conjunctions, which are finite in each case. Since an expression of this form can be written for each c_i which is not a peripheral afferent, we can, by substituting the corresponding expression in (1) for each N_jm or N_in, whose neuron is not a peripheral afferent, and repeating the process on the result, ultimately come to an expression for N_i in terms solely of peripherally afferent N, since 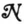IF1 is without circles. Moreover, this expression will be a TPE since obviously (1) is, and it follows immediately from the definition that the result of substituting a TPE for a constituent p(z) in a TPE is also one.

Theorem II.

Every TPE is realizable by a net of order zero.

The functor S obviously commutes with disjunction, conjunction, and negation. It is obvious that the result of substituting any S_i, realizable in the narrow sense (i.n.s.), for the p(z) in a realizable expression S₁, is itself realizable i.n.s. ; one constructs the realizing net by replacing the peripheral afferents in the net for S_i by the realizing neurons in the nets for the S_i. The one neuron net realizes p_i(z₁) i.n.s., and Figure 1-a shows a net that realizes Sp₁(z₁) and hence SS₂, i.n.s., if S₂ can be realized i.n.s. Now if S₂ and S₃ are realizable, then S^m S₂ and S^m S₃ are realizable i.n.s., for suitable m and n. Hence so are S^m+n S₂, and Sⁿ S₃. Now the nets of Figures lb, c, and d respectively realize S(p₁(z₁) v *p₂(z₁)), S(p₁(z₁). p₂(z₁)), and S(p₁(z₁).∾ p₂(z₁)) i.n.s. Hence S^m+n+1 (S₁ * v *S**₂), S^m+n+1 (S₁ . S₂), and S^m+n+1 (S₁. ∾ S₂) are realizable i.n.s. Therefore S₁ v S₂ S₁ . S₂ S₁ . ∾ S₂, are realizable if S₁ and S₂ are. By complete induction, all TPE are realizable. In this way, all nets may be regarded as built out of the fundamental elements of Figures 1a, b, c, d, precisely as the temporal propositional expressions are generated out of the operations of precession, disjunction, conjunction, and conjoined negation. In particular, corresponding to any description of state or distribution of the values true and false for the actions of all the neurons of a net save that which makes them all false, a single neuron is constructible whose firing is a necessary and sufficient condition for the validity of that description. Moreover, there is always an indefinite number of topologically different nets realizing any TPE.

Theorem III.

Let there be given a complex sentence S_x built up in any manner out of elementary sentences of the form p(Z₁ − zz) where zz is any numeral, by any of the propositional connections: negation, disjunction, conjunction, implication, and equivalence. Then S₁ is a TPE and only if it is false when its constituent p(z − zz) are all assumed false—i.e., replaced by false sentences — or that the last line in its truth-table contains an ‘F,’—or there is no term in its Hilbert disjunctive normal form composed exclusively of negated terms.

These latter three conditions are of course, equivalent (3). We see by induction that the first of them is necessary since p(z₁ − zz) becomes false when it is replaced by a false sentence, and S₁ v S₂ S₁. S₂, and S₁ ∾ S₂, are all false if both their constituents are. We see that the last condition is sufficient by remarking that a disjunction is a TPE when its constituents are and that any term.

S₁ . S₂. . . .S_m.∾S_m+1.∾. . . .∾S_n

can be written as

(S₁ . S₂. . . .S_m).∾(S_m+1 v S_m+2 v . . . . v S_n),

which is clearly a TPE.

The method of the last theorems does, in fact, provide a very convenient and workable procedure for constructing nervous nets to order, for those cases where there is no reference to events indefinitely far in the past in the specification of the conditions. By way of example, we may consider the possibility of heat produced by a transient cooling.

If a cold object is held to the skin for a moment and removed, a sensation of heat will be felt; if it is applied for a longer time, the sensation will be only of cold, with no preliminary warmth, however transient. It is known that one cutaneous receptor is affected by heat, and another by cold. If we let N₁ and N₂ be the actions of the respective receptors and N₃ and N₄ of neurons whose activity implies a sensation of heat and cold, our requirements may be written as

N₃(t) :≡: N₁(t−1) .v. N₂(t−3) . ∾ N₂(t−2)

N₄(t) .≡. N₂(t−2) . N₂(t−1)

where we suppose for simplicity that the required persistence in the sensation of cold is, say, two synaptic delays, compared with one for that of heat. These conditions clearly fall under Theorem III. A net may consequently be constructed to realize them by the method of Theorem II. We begin by writing them in a fashion which exhibits them as built out of their constituents by the operations realized in Figures la, b, c, d: i.e., in the form

N₃(t) .≡. S{N₁(t)* v ***S[(SN₂(t)) . ∾ N₂(t)]}

N₄(t) .≡. S{[SN₂(t)] . N₂(t)}.

First, we construct a net for the function enclosed in the greatest number of brackets and proceed outward; in this case, we run a net of the form shown in Figure 1a from c₂ to some neuron c_a, say, so that.

N_a(t) .≡. SN₂(t).

Next, introduce two nets of the forms 1c and 1d, both running from c_a and c₂ and ending respectively at c₄ and say c_b. Then

N₄(t) .≡. S[N_a(t) . N2(t)] .≡. S[(SN₂(t)) . N₂(t)].

N_b(t) .≡. S[N_a(t) . ∾ N2(t)] .≡. S[(SN₂(t)) . ∾ N₂(t)].

Finally, run a net of the form 1b from c₁ and c_b to c₃, and derive

N₃(t) .≡. S[N₁(t)* v ***N_b(t)]

.≡. S{N₁(t)* v ***S[(SN₂(t)] . ∾ N₂(t)}.

These expressions for N₃(t) and N₄(t) are the ones desired; and the realizing net in toto is shown in Figure 1e.

This illusion makes very clear the dependence of the correspondence between perception and the “external world” upon the specific structural properties of the intervening nervous net. The same illusion, of course, could also have been produced under various other assumptions about the behavior of the cutaneous receptors, with correspondingly different nets.

We shall now consider some theorems of equivalence: i.e., theorems which demonstrate the essential identity, save for time, of various alternative laws of nervous excitation. Let us first discuss the case of relative inhibition. By this we mean the supposition that the firing of an inhibitory synapse does not absolutely prevent the firing of the neuron, but merely raises its threshold, so that a greater number of excitatory synapses must fire concurrently to fire it than would otherwise be needed. We may suppose, losing no generality, that the increase in threshold is unity for the firing of each such synapse; we then have the theorem:

Theorem IV.

Relative and absolute inhibition are equivalent in the extended sense.

We may write out a law of nervous excitation after the fashion of (1), but employing the assumption of relative inhibition instead; inspection then shows that this expression is a TPE. An example of the replacement of relative inhibition by absolute is given by Figure 1f. The reverse replacement is even easier; we give the inhibitory axons afferent to c_i any sufficiently large number of inhibitory synapses apiece.

Second, we consider the case of extinction. We may write this in the form of a variation in the threshold θ_i; after the neuron c_i has fired; to the nearest integer — and only to this approximation is the variation in threshold significant in natural forms of excitation — this may be written as a sequence θ_i + b_j for j synaptic delays after firing, where b_j = 0 for j large enough, say j = M or greater. We may then state

Theorem V.

Extinction is equivalent to absolute inhibition.

For, assuming relative inhibition to hold for the moment, we need merely run M circuits 𝒯₁, 𝒯₂, … 𝒯_M containing respectively 1, 2 , …, M neurons, such that the firing of each link in any is sufficient to fire the next, from the neuron c_i back to it, where the end of the circuit 𝒯_i has just b_j inhibitory synapses upon c_i. It is evident that this will produce the desired results. The reverse substitution may be accomplished by the diagram of Figure 1g. From the transitivity of replacement, we infer the theorem. To this group of theorems also belongs the well-known.

Theorem VI.

Facilitation and temporal summation may be replaced by spatial summation.

This is obvious: one need merely introduce a suitable sequence of delaying chains, of increasing numbers of synapses, between the exciting cell and the neuron whereon temporal summation is desired to hold. The assumption of spatial summation will then give the required results. See, e.g., Figure 1h. This procedure had application in showing that the observed temporal summation in gross nets does not imply such a mechanism in the interaction of individual neurons.

The phenomena of learning, which are of a character persisting over most physiological changes in nervous activity, seem to require the possibility of permanent alterations in the structure of nets. The simplest such alteration is the formation of new synapses or equivalent local depressions of threshold. We suppose that some axonal terminations cannot at first excite the succeeding neuron, but if at any time the neuron fires, and the axonal terminations are simultaneously excited, they become synapses of the ordinary kind, henceforth capable of exciting the neuron. The loss of an inhibitory synapse gives an entirely equivalent result. We shall then have

Theorem VII.

Alterable synapses can be replaced by circles.

This is accomplished by the method of Figure 1i. It is also to be remarked that a neuron which becomes and remains spontaneously active can likewise be replaced by a circle, which is set into activity by a peripheral afferent when the activity commences, and inhibited by one when it ceases.

The Theory: Nets with Circles.

The treatment of nets which do not satisfy our previous assumption of freedom from circles is very much more difficult than that case. This is largely a consequence of the possibility that activity may be set up in a circuit and continue reverberating around it for an indefinite period of time, so that the realizable Pr may involve reference to past events of an indefinite degree of remoteness. Consider such a net 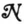IF1 , say of order p, and let c₁, c₂ , …, c_p be a cyclic set of neurons of 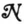IF1 . It is first of all clear from the definition that every N₃ of 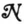IF1 can be expressed as a TPE, of N₂, N₂, …, N_p and the absolute afferents; the solution of 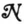IF1 involves then only the determination of expressions for the cyclic set. This done, we shall derive a set of expressions [A] :

N_i(z₁) .≡. Pr_i[Sⁿ⁺¹ N₁(z₁), Sⁿ⁺² N₂(z₁), …, S^n+p N_p(z₁)], (2)

where Pr_i also involves peripheral afferents. Now if n is the least common multiple of the n_ij, we shall, by substituting their equivalents according to (2) in (3) for the N_j, and repeating this process often enough on the result, obtain S of the form

N_i(z₁) .≡. Pr_i[Sⁿ N₁(z₁), Sⁿ N₂(z₁), …, Sⁿ N_p(z₁)]. (3)

These expressions may be written in the Hilbert disjunctive normal form as

N_{i} (Z_{1}) . \equiv . \underset{\binom{a ε κ}{β ε κ}}{Σ} S_{a} \underset{j ε κ}{Π} S^{n} N_{j} (z_{1}) \underset{j ε β}{Π} \infty S^{n} N_{j} (z_{1}), f o r s u i t a b l e κ (4)

where S_a is a TPE of the absolute afferents of 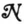IF1 . There exist some 2^p different sentences formed out of the p N_i by conjoining to the conjunction of some set of them the conjunction of the negations of the rest. Denumerating these by X₁(z₁), X₂(z₁), …, X_2*p*(z₁), we may, by use of the expressions (4), arrive at an equipollent set of equations of the form

X_{i} (z_{1}) . \equiv . \sum_{j = 1}^{2 P} {Pr}_{i j} (z_{1}) . S^{n} X_{j} (z_{1}) . (5)

Now we import the subscripted numerals i,j into the object language: i.e., define Pr₁ and Pr₂ such that Pr₁ (zz₁,z₁).≡.X_i(z₁) and Pr₂(zz₁, zz₂, z₁) .≡. Pr_ij(Z₁) are provable whenever zz₁ and zz₂ denote i and j respectively.

Then we may rewrite (5) as

(z₁) zz_p : Pr₁(z₁, z₃)

.≡. (Ez₂)zz_p . Pr₂ (z₁, z₂, z₃ − zz_*n*) . Pr₁, (z₂, z₃ − zz_n) (6)

where zz_n denotes n and zz_p denotes 2^p. By repeated substitution, we arrive at an expression

(z₁)zz_p: Pr₁ (z₁, zz_n zz₂) .≡. (Ez₂)zz_p (Ez₃)zz_p…(Ez_n)zz_p . Pr₂(z₁, z₂, zz_n(zz₂ − l)) . Pr₂(z₂, z₃, zz_n(zz₂ − 1)). . . . (7)

Pr₂(z_n-1, z_*n*, 0).Pr₁(z_n, 0), for any numeral zz₂ which denotes s.

This is easily shown by induction to be equipollent to

(z₁)zz_p: Pr₁(z₁, z_n zz₂) :≡: (Ef) (z₂)zz₂ − 1 f(z₂, zz_n) ≦ zzp . f (zz_n zz₂) = z₁ . Pr₂(f(zz_n, (z₂+1)), f(zz_n zz₃)) . Pr₁(f(0), 0) (8)

and since this is the case for all zz₂, it is also true that

(z₄) (z₁)zz_p : Pr₁(z₁, z₄) :≡: (Ef) (z₂)(z₄ − 1) . f(z₂) ≦ zz_p . f(z₄) = z₁ f (z₄) = (z₁) . Pr₂[f(z₂+1), f(z₂), z₂]. Pr₁[f(res(z₄, zz_n)), res(z₄, zz_n)], (9)

where zz_n denotes n, res (r,s) is the residue of r mod s, and zz_p denotes 2^p. This may be written in a less exact way as

N_i(t) .≡. (Eϕ) (x)t−1. ϕ(x) ≦ 2^p . ϕ(t) = i . P [ϕ(x + 1), ϕ(x) . N _ϕ(0) (0)],

where x and t are also assumed divisible by n, and Pr₂ denotes P. From the preceding remarks, we shall have

Theorem VIII.

The expression (9) for neurons of the cyclic set of a net 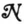IF1 together with certain TPE expressing the actions of other neurons in terms of them, constitute a solution of IF1 .

Consider now the question of the realizability of a set S_i. A first necessary condition, demonstrable by an easy induction, is that

\begin{matrix} (z_{2}) z_{1} . p_{1} (z_{2}) \equiv p_{2} (z_{2}) . \to . S_{i} \equiv S_{i} {\begin{array}{l} p_{1} \\ p_{2} \end{array}} (10) \end{matrix}

should be true, with similar statements for the other free p in S_i: i.e., no nervous net can take account of future peripheral afferents. Any S_i satisfying this requirement can be replaced by an equipollent S of the form

(Ef) (z₂) z₁ (z₃) zz_p : fε Pr_mi

: f(z₁, z₂, z₃) = 1 . = . p_x4(z₂) (11)

where zz_p denotes p, by defining

\underset{m i}{Pr} = \overset{Λ}{f} [(z_{1}) (z_{2}) (z_{1}) (z_{3}) z z_{p} : . f (z_{1}, z_{2}, z_{3}) = 0. v . f (z_{1}, z_{2}, z_{3}) = 1 : f (z_{1}, z_{2}, z_{3}) = 1. \equiv . p_{z 2} (z_{2}) : \to : S_{i}] .

Consider now these series of classes α_i, for which

N_i(t) :≡: (Eϕ) (x)t(m)q : ϕεα_i : N_m(x) .≡. ϕ(t, x, m) = 1 . [ = q + 1, …, M (12)

holds for some net. These will be called prehensible classes. Let us define the Boolean ring generated by a class of classes κ as the aggregate of the classes which can be formed from members of κ by repeated application of the logical operations ; i.e., we put

ℜ (κ) = p^{'} \overset{Λ}{λ} [(α, β) : α ε κ \to α ε λ : α, β ε λ . \to . - α, α . β, α v β ε λ] .

We shall also define

\begin{array}{l} \overset{―}{ℜ} (κ) . = . ℜ (κ) - ι^{'} p^{'} -^{″} κ, \\ ℜ_{e} (κ) = p^{'} \overset{Λ}{λ} [(α, β) : α ε κ \to α ε λ . \to . - α, α . β, α v β, S α ε λ] \\ {\overset{―}{ℜ}}_{e} (κ) = ℜ_{e} (κ) - ι^{'} p^{'} -^{″} κ, \end{array}

and

σ (ψ, t) = \overset{Λ}{ϕ} [(m) . ϕ (t + 1, t, m) = ψ (m)] .

The class ℛ_e(κ) is formed from κ in analogy with ℛ(κ), but by repeated application not only of the logical operations but also of that which replaces a class of properties P ε α by S(P)ε S “α. We shall then have the

LEMMA

Pr₁ (p₁, p₂,…, p_m, z₁) is a TPE if and only if

\begin{array}{l} (z_{1}) (p_{1}, . . ., p_{m}) (E p_{m + 1}) : p_{m + 1} ε {\bar{ℜ}}_{e} ({p_{1}, p_{2}, . . ., p_{m}}) \\ p_{m + 1} (z_{1}) \equiv \underset{1}{Pr} (p_{1}, p_{2}, . . ., p_{m}, z_{1}) (13) \end{array}

is true; and it is a TPE not involving ‘S’ if and only if this holds when ‘ℛ̅_e’ is replaced by ‘ℛ̅,’ and we then obtain

Theorem IX.

A series of classes α₁ , α₂, … α_s is a series of prehensible classes if and only if

\begin{array}{l} (E m) (E n) (p) n (i) (ψ) : . (x) m ψ (x) = 0 v ψ (x) = 1 : (E β) \\ (E y) m . ψ (y) = 0. β ε ℜ [\overset{Λ}{γ} ((E i) . γ = α_{i})) . v . (x) m . \\ ψ (x) = 0. β ε \overset{―}{ℜ} [\overset{Λ}{γ} ((E i) . γ = α_{i})] : (t) (ϕ) : ϕ ε a_{i} . (14) \\ σ (ϕ, n t + p) . \to . (E f) . f ε β . (w) m (x) t - 1. \\ ϕ (n (t + 1) + p, n x + p, w) = f (n t + p, n x + p, w) . \end{array}

The proof here follows directly from the lemma. The condition is necessary, since every net for which an expression of the form (4) can be written obviously verifies it, the ψ's being the characteristic functions of the S_a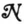β $\mathop {II}\limits_{i\varepsilon a}$ Pr_i $\mathop {II}\limits_{j\varepsilon \beta a}$ Pr_j, where Pr_k denotes α_k for all k. Conversely, we may write an expression of the form (4) for a net IF1 fulfilling prehensible classes satisfying (14) by putting for the Pr_a Pr denoting the ψ's, and a Pr, written in the analogue for classes of the disjunctive normal form, and denoting the a corresponding to that ψ, conjoined to it. Since every S of the form (4) is clearly realizable, we have the theorem.

It is of some interest to consider the extent to which we can, by knowledge of the present, determine the whole past of various special nets: i.e., when we may construct a net, the firing of the cyclic set of whose neurons requires the peripheral afferents to have had a set of past values specified by given functions ϕ_i. In this case, the classes α_i of the last theorem reduced to unit classes; and the condition may be transformed into

\begin{array}{l} (E m, n) (p) n (i, ψ) (E j) : . (x) m : ψ (x) = 0. v . ψ (x) = 1 : \\ ϕ_{i} ε σ (ψ, n t + p) : \to : (w) m (x) t - 1. ϕ_{i} (n (t + 1) \\ + p, n x + p, w) = ϕ_{i} (n t + p, n x + p, w) : . \\ (u, v) (w) m . ϕ_{i} (n (u + 1) + p, n u + p, w) \\ = ϕ_{i} (n (v + 1) + p, n v + p, w) . \end{array}

On account of limitations of space, we have presented the above argument very sketchily; we propose to expand it and certain of its implications in a further publication.

The condition of the last theorem is fairly simple in principle, though not in detail; its application to practical cases would, however, require the exploration of some 2²ⁿ classes of functions, namely the members of ℛ({α₁, …, α_s}). Since each of these is a possible β of Theorem IX, this result cannot be sharpened. But we may obtain a sufficient condition for the realizability of an S, which is very easily applicable and probably covers most practical purposes. This is given by

Theorem X.

Let us define a set K of S by the following recursion:

Any TPE and any TPE whose arguments have been replaced by members of K belong to K;
If Pr₁ is a member of K, then (z₂)z₁ . Pr₁(z₂), (Ez₂)z₁ . Pr₁(z₂), and C_mn(z₁) . s belong to it, where C_mn denotes the property of being congruent to m modulo n, m < n.
The set Κ has no further members

Then every member of Κ is realizable.

For, if Pr₁(z₁) is realizable, nervous nets for which

N_i(z₁) .≡. Pr₁(z₁) . SN_i(z₁)

N_i(z₁) .≡. Pr₁(z₁) v SN_i(z₁)

are the expressions of equation (4), realize (z₂)z₁. Pr₁(z₂) and (E z₂)z₁ . Pr₁(z₂) respectively; and a simple circuit, c₁, c₂ … c_n, of n links, each sufficient to excite the next, gives an expression

N_m(z₁) .≡. N₁(0) . C_mn

for the last form. By induction, we derive the theorem.

One more thing is to be remarked in conclusion. It is easily shown: first, that every net, if furnished with a tape, scanners connected to afferents, and suitable efferents to perform the necessary motor-operations, can compute only such numbers as can a Turing machine; second, that each of the latter numbers can be computed by such a net; and that nets with circles can be computed by such a net; and that nets with circles can compute, without scanners and a tape, some of the numbers the machine can, but no others, and not all of them. This is of interest as affording a psychological justification of the Turing definition of computability and its equivalents, Church's λ — definability, and Kleene's primitive recursiveness: If any number can be computed by an organism, it is computable by these definitions, and conversely.

Consequences

Causality, which requires description of states and a law of necessary connection relating them, has appeared in several forms in several sciences, but never, except in statistics, has it been as irreciprocal as in this theory. Specification for any one time of afferent stimulation and of the activity of all constituent neurons, each an “all-or-none” affair, determines the state. Specification of the nervous net provides the law of necessary connection whereby one can compute from the description of any state that of the succeeding state, but the inclusion of disjunctive relations prevents complete determination of the one before. Moreover, the regenerative activity of constituent circles renders reference indefinite as to time past. Thus our knowledge of the world, including ourselves, is incomplete.

As to space and indefinite as to time. This ignorance, implicit in all our brains, is the counterpart of the abstraction which renders our knowledge useful. The role of brains in determining the epistemic relations of our theories to our observations and of these to the facts is all too clear, for it is apparent that every idea and every sensation is realized by activity within that net and by no such activity are the actual afferents fully determined.

There is no theory we may hold and no observation we can make that will retain so much as its old defective reference to the facts if the net be altered. Tinitus, paraesthesias, hallucinations, delusions, confusions, and disorientations intervene. Thus empiry confirms that if our nets are undefined, our facts are undefined, and to the “real,” we can attribute not so much as one quality or “form.” With determination of the net, the unknowable object of knowledge, the “thing in itself,” ceases to be unknowable.

To psychology, however, defined, specification of the net would contribute all that could be achieved in that field — even if the analysis were pushed to ultimate psychic units or “psychons,” for a psychon can be no less than the activity of a single neuron. Since that activity is inherently propositional, all psychic events have an intentional, or “semiotic,” character. The “all-or-none” law of these activities and the conformity of their relations to those of the logic of propositions ensure that the relations of psychons are those of the two-valued logic of propositions. Thus in psychology, introspective, behavioristic, or physiological, the fundamental relations are those of two-valued logic.

Expression for the Figures

In the figure, the neuron c_i is always marked with the numeral i upon the body of the cell, and the corresponding action is denoted by ‘N’ with i as subscript, as in the text.

Figure 1a N₂(t) .≡. N₁(t − 1)

Figure 1b N₃(t) .≡. N₁(t − 1) v N₂(t − 1)

Figure 1c N₃(t) .≡. N₁(t − 1) . N₂(t − 1)

Figure 1d N₃(t) .≡. N₁(t − 1) . ∾ N₂(t − 1)

Figure 1e N₃(t) :≡: N₁(t − 1) .**v** . N₂(t − 3) . ∾ N₂(t − 2)

N₄(t) :≡: N₂(t − 2) . N₂(t − 1)

Figure 1f N₄(t) :≡: ∾N₁(t − 1) . N₂(t − 1) v N₃(t − 1) . v . N₁(t − 1). N₂(t − 1) . N₃(t − 1)

N₄(t) :≡: ∾N₁(t − 2) . N₂(t − 2) v N₃(t − 2) . v . N₁(t − 2). N₂(t − 2) . N₃(t − 2)

Figure 1g N₃(t) .≡. N₂(t − 2) . ∾ N₁(t − 3)

Figure 1h N₂(t) .≡. N₁(t − 1) . N₁(t − 2)

Figure 1i N₃(t) :≡: N₂(t − 1) .v. N₁(t − 1).(Ex)t − 1 . N₁(x) . N₂(x)

Hence arise, constructional solutions of holistic problems involving the differentiated continuum of sense awareness and the normative, perfective, and resolvent properties of perception and execution. From the irreciprocity of causalit,y it follows that even if the net be known, though we may predict future from present activities, we can deduce neither afferent from central, nor central from efferent, nor past from present activities — conclusions which are reinforced by the contradictory testimony of eye-witnesses, by the difficulty of diagnosing differentially the organically diseased, the hysteric and the malingerer, and by comparing one's own memories or recollections with his contemporaneous records. Moreover, systems which so respond to the difference between afferents to a regenerative net and certain activity within that net as to reduce the difference exhibit purposive behavior; and organisms are known to possess many such systems, subserving homeostasis, appetition, and attention. Thus both the formal and the final aspects of that activity, which we are wont to call mental, are rigorously deducible from present neurophysiology. The psychiatrist may take comfort from the obvious conclusion concerning causality —that, for prognosis, history is never necessary. He can take little from the equally valid conclusion that his observables are explicable only in terms of nervous activities, which, until recently, have been beyond his ken. The crux of this ignorance is that inference from any sample of overt behavior to nervous nets is not unique, whereas, of imaginable nets, only one in fact exists, and may, at any moment, exhibit some unpredictable activity. Certainly, for the psychiatrist it is more to the point that in such systems, “Mind” no longer “goes more ghostly than a ghost.” Instead, diseased mentality can be understood without loss of scope or rigor in the scientific terms of neurophysiology. For neurology, the theory sharpens the distinction between nets necessary or merely sufficient for given activities and so clarifies the relations of disturbed structure to disturbed function. In its own domain, the difference between equivalent nets and nets equivalent in the narrow sense indicates the appropriate use and importance of temporal studies of nervous activity: and to mathematical biophysics, the theory contributes a tool for rigorous symbolic treatment of known nets and an easy method of constructing hypothetical nets of required properties.

Footnote

[^]: Reprinted from Bulletin of Mathematical Biophysics, Volume 5, 1943.

Literature

Carnap, R. 1938. The Logical Syntax of Language. New York: Harcourt, Brace and Company.

Russell, B., and Whitehead, A. N. 1925. Principa Mathematica. Cambridge: Cambridge University Press.

Hilbert, D., und Ackermann, W. 1927. Grundüge der Theoretischen Logik. Berlin: J. Springer.