THE UTILITY OF ANASTOMOTIC NETS12 [157]
W.S. McCulloch
##
Where many rivers make a common plain each branches into several channels that join branches of adjacent streams and, as this continues toward thfe sea, waters from all sources are so mixed that each of its many mouths spews some from every source.
The early Greek physicians likened our venous system to such a net, calling it ANASTOMOTIC. You have only to look at the back of your hand to see how apt the term.
We are, since the time of Harvey, inclined to speak similarly of arteries and to think the only reason for anastomosis is to insure circulation when one vessel is occluded. But Hippocrates and Empedocles held a cardio-centric theory of love and knowledge, last seriously defended thirty years ago by the neurosurgeon Dandy who insisted that consciousness resided in the left anterior cerebral artery. To the fathers of medicine knowledge consisted in an intimate mixture of the knower and the known, and the final mixing of all these mixtures in the heart. The nerves were only reins to govern muscles, and the brain was phlegm to cool the blood. Consequently, to them mixing was as Important as the preservation of communication. Except for things like hormones, we have transferred these functions from vessels to nerves and from heart to brain. Here we look for the anastomotic nets of nervous tissues, to preserve continuity and combine signals from all parts of the body. Today we know little about the nature of the signals and less about how they are combined. They are transmitted as trains of discrete impulses
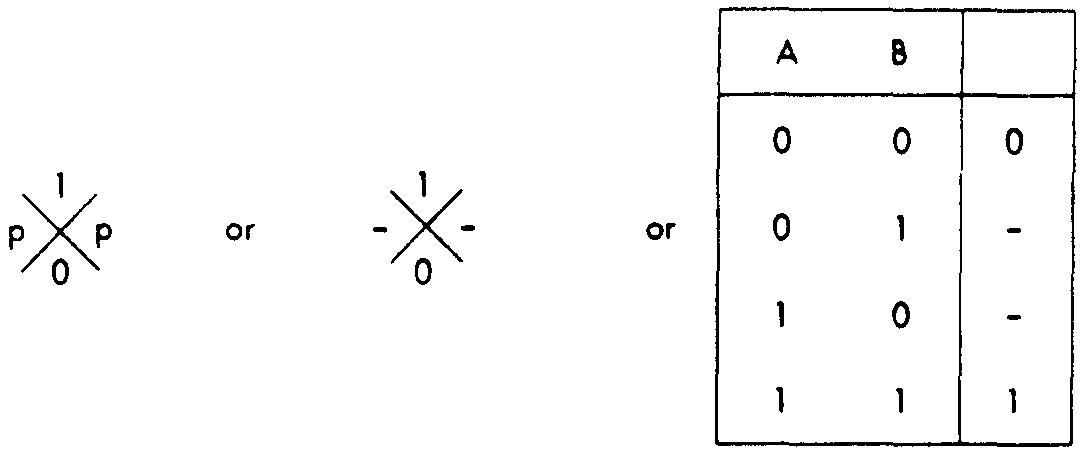
Figure 1.
propagated along the neuron's output fiber called its axon. This axon ends as branches on or near other neurons. These may excite or inhibit it. Moreover, they interact short of a recipient neuron so that impulses of one source may prevent those of another from reaching that neuron. The connections are numerous; nearly a quarter of a million axons may play upon a single large neuron.
I am not sure whether the mathematics exist or can be soon invented for an adequate quasi-continuous theory of these complexities. We have, therefore, begun by discovering the sort of logic required to handle the problem. It is probabilistic logic in von Neumann's sense, for the function, not merely the argument, is only probable. With six, or fewer, arguments we have found it most transparently represented by Venn's diagrams that embody the truth tables of the function computed by a neuron, with 1 for true, p for probably true, and 0 for false (Fig. 1).
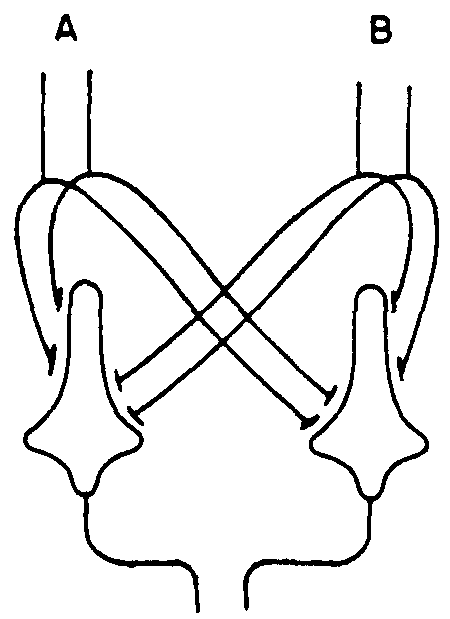
Figure 2.
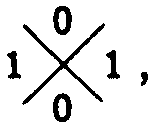
Moreover, when more than one axon transmits the same argument or function to one neuron, the logic has to have more than one truth value and is most obviously represented in bundles of parallel line representing the axons of the formal neurons (Fig. 2). Let me remark in passing that, although neurons are threshold components, we are not limited to threshold logic and can realistically schematize the computation of the exclusive or,
by the cells of the superior olive (Fig. 3). And we can construct diagrams of connections such that, in the functional Venn diagram of that neuron, the successive ones appear in any sequence we desire as its threshold decreases (Fig. 4). With these tools my collaborators will show, first, the zero error reliability in computation despite limited perturbation of threshold, signal strength or even connection and, second, with more general models something in computation resembling the information-theoretic rate of communication theory, treating all perturbations as if they were lumped on the axon. It remains for me only to speak of the other great utility of anastomotic nets—which arises not from their reliability but from their flexibility.

Figure 3.

Figure 4.
A net of 3 neurons with 2 inputs each with thresholds modulated by input from the net can be made to compute 15 of the 16 possible logical functions of two arguments and 4 neurons with 3 inputs each, 253 logical functions of 3 arguments. The number increases rapidly with the number of inputs per neuron (Fig. 5).
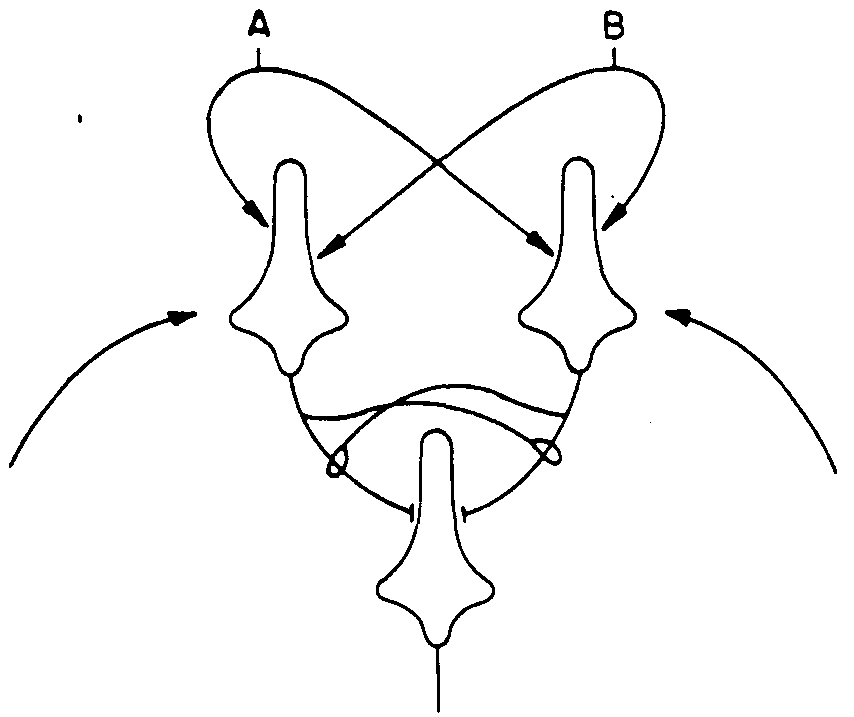
Figure 5.
The paper immediately following, by Blum, Onesto, and Verbeek, and the paper by Cowan and Winograd whose abstract appears on p. 377, are both extensions of this introductory paper by Professor McCulloch and describe work which was inspired by him.
Footnotes
For further research:
Wordcloud: Anastomotic, Appear, Arguments, Artery, Axon, Brain, Branches, Combine, Communication, Computation, Connections, Continues, Diagrams, Fig, Figure, Function, Grant, Heart, Impulses, Inc, Inputs, Knowledge, Limited, Logic, Mixing, Mixture, Moreover, Nerves, Net, Neuron, Number, Paper, Perturbation, Preserve, Probably, Reliability, Represented, Signals, Source, Speak, Systems, Theory, Threshold, Transmits, True, Truth, Utility, Venn, Vessel, Work
Keywords: Nets, Neuron, Knowledge, Love, Physicians, Streams, Tissues, Harvey, Truth, System
Google Books: http://asclinks.live/rbw3
Google Scholar: http://asclinks.live/7pak
Jstor: http://asclinks.live/6qtq