WHAT IS A NUMBER, THAT A MAN MAY KNOW IT, AND A MAN, THAT HE MAY KNOW A NUMBER?12 [153]
W.S. McCulloch
Introduction
Gentlemen: I am very sensible of the honor you have conferred upon me by inviting me to read this lecture. I am only distressed, fearing you may have done so under a misapprehension; for, though my interest always was to reduce epistemology to an experimental science, the bulk of my publications has been concerned with the physics and chemistry of the brain and body of beasts. For my interest in the functional organization of the nervous system that knowledge was as necessary as it was insufficient in all problems of communication in men and machines. I had begun to fear that the tradition of experimental epistemology I had inherited through Dusser de Barenne from Rudolph Magnus would die with me, but if you read What the Frog's Eye tells the Frog's Brain, written by Jerome Y. Lettvin, which appeared in the Proceedings of the Institute of Radio Engineers, November 1959, you will realize that the tradition will go on after I am gone. The inquiry into the physiological substrate of knowledge is here to stay until it is solved thoroughly; that is, until we have a satisfactory explanation of how we know what we know, stated in terms of the physics and chemistry, the anatomy and physiology, of the biological system. At the moment my age feeds on my youth—and both are unknown to you. It is not because I have reached what Oliver Wendell Holmes would call our anecdotage—but because all impersonal questions arise from personal reasons and are best understood from their histories—that I would begin with my youth.
I come of a family which, whether it be a corporeal or incorporeal hereditimentum, produces, with few notable exceptions, professional men and women—lawyers, doctors, engineers, and theologians. My older brother was a chemical engineer. I was destined for the ministry. Among my teen-age acquaintances were Henry Sloan Coffin, Harry Emerson Fosdick, H.K.W. Kumm, Hecker—of the Church of All Nations—sundry Episcopalian theologians, and that great Quaker philosopher, Rufus Jones.
In the fall of 1917 I entered Haverford College with two strings to my bow—facility in Latin and a sure foundation in mathematics. I “honored” in the latter and was seduced by it. That winter Rufus Jones call me in. “Warren,” said he, “what is Thee going to be?” and I said, “I don't know.” “And what is Thee going to do?” And again I said, “I have no idea; but there is one question I would like to answer. What is a number, that a man may know it, and a man, that he may know a number?” He smiled and said, “Friend, Thee will be busy as long as Thee lives.” I have been, and that is what we are about.
That spring I joined the Naval Reserve, and for about a year of active duty, worked on problems of submarine listening, marlinspike seamanship, and semaphore, ending at Yale in the Officers’ Training School, where my real function was to teach celestial navigation. I stayed there, majoring in philosophy, minoring in psychology, until I graduated and went to Columbia, took my M.A. in psychology, working on experimental aesthetics, and then to its medical school, for the sole purpose of understanding the physiology of the nervous system, at which I have labored ever since.
It was in 1919 that I began to labor chiefly on logic, and by 1923 I had attempted to manufacture a logic of transitive verbs. In 1928 I was in neurology at Bellevue Hospital and in 1930 at Rockland State Hospital for the Insane, but my purpose never changed. It was then that I encountered Eilhard von Domarus, the great philosophic student of psychiatry, from whom I learned to understand the logical difficulties of true cases of schizophrenia and the development of psychopathia—not merely clinically, as he had learned them of Berger, Birnbaum, Bumke, Hoche, Westphal, Kahn, and others—but as he understood them from his friendship with Bertrand Russell, Heidegger, Whitehead, and Horthrop—under the last of whom he wrote his great unpublished thesis, The Logical Structure of Mind—An Inquiry into the Philosophical Foundations of Psychology and Psychiatry. It is to him and to our mutual friend, Charles Holden Prescott, that I am chiefly indebted for my understanding of paranoia vera and of the possibility of making the scientific method applicable to systems of many degrees of freedom. From Rockland I went back to Yale's Laboratory of Neurophysiology to work with the erstwhile psychiatrist, Dusser de Barenne, on experimental epistemology; and only after his death, when I had finished the last job on strychnine neuronography to which he had laid his hand, did I go to Illinois as a Professor of Psychiatry, always pursuing the same theme, especially with Walter Pitts. I was there 11 years working physiology in terms of anatomy, physics, and chemistry until, in 1952, I went to the Research Laboratory of Electronics of the Massachusetts Institute of Technology to work on the circuit theory of brains. Granted that I have never relinquished my interest in empiricism and am chiefly interested in the condition of water in living systems—witness the work of my collaborator, Berendsen, on nuclear magnetic resonance—it is with my ideas concerning number and logic, before 1917 and after 1952, that we are now concerned.
II
This lecture might be called, In Quest of the Logos or, more appropriately, perverting St. Bonaventura's famous title, An Itinerary to Man. Its proper preface is that St. Augustine says that it was a pagan philosopher—a Neoplatonist—who wrote, “In the beginning was the Logos, without the Logos was not anything made that was made....” So begins our Christian Theology. It rests on four principles. The first is the Eternal Verities. Listen to the thunder of that Saint, in about A.D. 500, “7 and 3 are 10; 7 and 3 have always been 10; 7 and 3 at no time and in no way have ever been anything but 10, 7 and 3 will always be 10; I said that these indestructible truths of arithmetic are common to all who reason.” An Eternal Verity, any corner stone of theology, is a statement that is true regardless of the time and place of its utterance. Each he calls an Idea in the Mind of God, which we can understand but can never comprehend. His examples are drawn chiefly from arithmetic, geometry, and logic, but he includes what we would now call the Laws of Nature, according to which God created the world. Yet he did not think all men equally gifted, persistent, or perceptive to grasp their ultimate consequences, and he was fully aware of the pitfalls along the way. The history of western science would have been no shock to his Theology. That it took a Galileo, a Newton, and an Einstein to eventually lead us to a tensor invariant, as it did, fits well with his theory of knowledge and of truth. He would expect most men to understand ratio and proportion, but few to suspect the categorical implications of a supposition that simultaneity was not defined for systems moving with respect to one another. There is one passage that I can only understand by supposing that he knew well why the existence of horn angles had compelled Euclid's shift to Eudoxus’ definition of ratio (I think it's in the fifth book) for things may be infinite with respect to one another and thence have no ratio. Be that as it may, we come next to authority.
Among the scholastic philosophers it is always in a suspect position. There are always questions of the corruption of the text; there are always questions of interpretations or of translations from older forms, or older meanings of the words, even of grammatical constructions. And who were the authorities? Plato, of course, and many a Neoplatonist and, later, Aristotle, known chiefly through the Arabs. Which others are accepted depends chiefly on the date, the school, and the question at issue. But the rules of right reason were fixed. One established first his logic—a realistic logic—despite nominalistic criticism such as Peter Abelard's, despite the Academicians invoking Aristotle's accusation of Plato that “he multiplied his worlds,” a conclusion at variance with modern logical decisions and sometimes at variance with the Church. After logic, came being—ontology if you will, for being is a matter of definition, without which one never knows about what he speaks. To this, the apparent great exception is Thomas Aquinas who takes existence as primary. This gives mere fact priority over the Verities and tends to make his logic, although realistic, a consequence of epistemology; that is to put fact ahead of reason and truth after it. Perhaps for this reason, although Roman law is clearly Stoic, he quotes Cicero more often than any other authority. His “God, in whom we live and move and have our being,” is the existent. Therefore He alone knows us as we know ourselves. Consciousness, being an agreement of witnesses, becomes conscience, for while we may fool others, we cannot fool God; one ought to act as God knows him. The result is good ethics, but little contribution to science. His conception fits the Roman requirement of the agreement of witnesses required by Law, as at the trial of Christ—and today in forensic medicine—but not the scientist's requirement, who, in the moment of discovery is the only one who knows the very thing he knows and has to wait until God agrees with him.
From that saint's day on, the battle rages between the Platonists and the Aristotelians. But the fourth principle in Theology begins to take first place—witness Roger Bacon. One has the Eternal Verities (logic, mathematics, and to a less extent, the Laws of Nature). One has the Authorities whom one tests against the Verities by reason—and there, in the old sense, ended the “experiment.” In the new sense one had to look again at Nature for its Laws, for they also are Ideas in the Mind of the Creator. Of Roger Bacon's outstanding knowledge of mathematics and logic there can be no doubt, but his observations are such that one suspects he had invented some sort of telescope and microscope. Natural Law began to grow. Duns Scotus was its last scholastic defender, and the last to insist on realistic logic, without which there is no science of the world. His subtle philosophy makes full use of Aristotle's logic and shows well its limitation. Deductions lead from rules and cases to facts—the conclusions. Inductions lead toward truth, with less assurance, from cases and facts, toward rules as generalizations, valid for bound causes, not for accidents. Abductions, the Apagoge of Aristotle, lead from rules and facts to the hypothesis that the fact is a case under the rule. This is the breeding place of scientific ideas to be tested by experiment. To these we shall return later; for, nudged by Chaos, they are sufficient to account for intuition or insight, or invention. There is no other road toward truth. Through this period the emphasis had shifted from the Eternal Verities of mathematics and logic to the Laws of Nature.
Hard on the heels of Duns Scotus trod William of Ockham, greatest of nominalists. He quotes Entia non sint multiplicanda praeter necessitatem against the multiplicity of entities necessary for Duns’ subtleties. He demands that there be no collusion of arguments from the stern realities of logic with the stubbornnesses of fact. His intent is to reach deductive conclusions with certainty, but he suspected that the syllogism is a strait jacket. Of course he recognized that, and I quote him, “man thinks in two kinds of terms: one, the natural terms, shared with beasts; the other, the conventional terms (the logicals) enjoyed by man alone.” By Ockham, logic, and eventually mathematics, are uprooted from empirical science. To ensure that nothing shall be in the conclusion that is not in the premise bars two roads that lead to the truth of the world and reduces the third road to the vacuous truth of circuitous tautology.
‘δ αύròs λóyos.’
It is clear on reading him that he only sharpened a distinction between the real classes and classes of real things, but it took hold of a world that was becoming empirical in an uncritical sense. It began to look on logic as a sterile fugling with mere words and numbers, whereas truth was to be sought from experiment among palpable things. Science in this sense was born. Logic decayed. Law usurped the throne of Theology, and eventually Science began to usurp the throne of Law. Not even the intellect of Leibnitz could lee-bow the tide. Locke confused the ideas of Newton with mere common notions. Berkeley, misunderstanding the notions of objectivity for an excess of subjectivity, committed the unpardonable sin of making God a deus ex machina, who, by perennial awareness, kept the world together where and when we had no consciousness of things.
David Hume revolted. Left with only a succession of perceptions, not a perception of succession, causality itself for him could be only “a habit of the mind.” Compare this with Duns Scotus’ following proposition reposing in the soul: “Whatever occurs as in a great many things from some cause which is not free, is the natural effect of that cause.” Clearly Hume lacked the necessary realistic logic; and his notions awoke Kant from his dogmatic slumbers—but only to invent a philosophy of science that takes epistemology as primary, makes ontology secondary, and ends with a logic in which the thing itself is unknown, and perception itself embodies a synthetic a priori. Doubtless his synthetic a priori has been the guiding star of the best voyages on the sea of “stimulus-equivalence.” But more than once it has misguided us in the field of physics—perhaps most obviously when we ran head-on into antimatter, which Leibnitz’ ontology and realistic logic might have taught us to expect.
What is much worse than this is the long neglect of Hume's great gift to mathematics. At the age of 23 he had already shown that only in logic and arithmetic can we argue through any number of steps, for only here have we the proper test. “For when a number hath a unit answering to an unit of the other we pronounce them equal.”
Bertrand Russell was the first to thank Hume properly, and so to give us the usable definition, not merely of equal numbers, but of number: “A number is the class of all of those classes that can be put into one-to-one correspondence to it.” Thus 7 is the class of all those classes that can be put into one-to-one correspondence with the days of the week, which are 7. Some mathematicians may question whether or not this is an adequate definition of all that the mind of man has devised and calls number; but it suffices for my purpose, for what in 1917 I wanted to know was how it could be defined so that a man might know it. Clearly, one cannot comprehend all the classes that can be put into one-to-one correspondence with the days of the week, but man understands the definition, for he knows the rule of procedure by which to determine it on any occasion. Duns Scotus has proved this to be sufficient for a realistic logic. But please note this: The numbers from 1 through 6 are perceptibles; others, only countables. Experiments on many beasts have often shown this: 1 through 6 are probably natural terms that we share with the beasts. In this sense they are natural numbers. All larger integers are arrived at by counting or putting pebbles in pots or cutting notches in sticks, each of which is—to use Ockham's phrase—a conventional term, a way of doing things that has grown out of our ways of getting together, our communications, our logos, tricks for setting things into one-to-one correspondence.
We have now reached this point in the argument. First, we have a definition of number which is logically useful. Second, it depends upon the perception of small whole numbers. Third, it depends upon a symbolic process of putting things into one-to-one correspondence in a conventional manner. Such then is the answer to the first half of the question. The second is much more difficult. We know what a number is that a man may know it, but what is a man that he may know a number?
III
Please remember that we are not now concerned with the physics and chemistry, the anatomy and physiology, of man. They are my daily business. They do not contribute to the logic of our problem. Despite Ramon Lull's combinatorial analysis of logic and all of his followers, including Leibnitz with his universal characteristic and his persistent effort to build logical computing machines, from the death of William of Ockham logic decayed. There were, of course, teachers of logic. The forms of the syllogism and the logic of classes were taught, and we shall use some of their devices, but there was a general recognition of their inadequacy to the problems in hand. Russell says it was Jevons—and Feibleman, that it was DeMorgan—who said, “The logic of Aristotle is inadequate, for it does not show that if a horse is an animal then the head of the horse is the head of an animal.” To which Russell replies,—“Fortunate Aristotle, for if a horse were a clam or a hydra it would not be so.” The difficulty is that they had no knowledge of the logic of relations, and almost none of the logic of propositions. These logics really began in the latter part of the last century with Charles Pierce as their great pioneer. As with most pioneers, many of the trails he blazed were not followed for a score of years. For example, he discovered the amphecks—that is, ⌝not both … and …⌜ and⌝neither … nor ⌜, which Sheffer rediscovered and are called by his name for them, “stroke functions.” It was Pierce who broke the ice with his logic of relatives, from which springs the pitiful beginnings of our logic of relations of two and more than two arguments. So completely had the traditional Aristotelian logic been lost that Pierce remarks that when he wrote the Century Dictionary he was so confused concerning abduction, or Apagoge, and induction that he wrote nonsense. Thus Aristotelian logic, like the skeleton of Tom Paine, was lost to us from the world it had engendered. Pierce had to go back to Duns Scotus to start again the realistic logic of science. Pragmatism took hold, despite its misinterpretation by William James. The world was ripe for it. Frege, Peano, Whitehead, Russell, Wittgenstein, followed by a host of lesser lights, but sparked by many a strange character like Schroeder, Sheffer, Gödel, and company, gave us a working logic of propositions. By the time I had sunk my teeth into these questions, the Polish school was well on its way to glory. In 1923 I gave up the attempt to write a logic of transitive verbs and began to see what I could do with the logic of propositions. My object, as a psychologist, was to invent a kind of least psychic event, or “psychon,” that would have the following properties. First, it was to be so simple an event that it either happened or else it did not happen. Second, it was to happen only if its bound cause had happened—shades of Duns Scotus!—that is, it was to imply its temporal antecedent. Third, it was to propose this to subsequent psychons. Fourth, these were to be compounded to produce the equivalents of more complicated propositions concerning their antecedents.
In 1929 it dawned on me that these events might be regarded as the all-or-none impulses of neurons, combined by convergence upon the next neuron to yield complexes of propositional events. During the nineteen-thirties, first under influences from F.H. Pike, C.H. Prescott, and Eilhard von Domarus, and later, Northrop, Dusser de Barenne, and a host of my friends in neurophysiology, I began to try to formulate a proper calculus for these events by subscripting symbols for propositions in some sort of calculus of propositions (connected by implications) with the time of occurrence of the impulse in each neuron. My then difficulties were five fold: 1) There was at that time no workable notion of inhibition, which had entered neurophysiology from clerical orders to desist. 2) There was a confusion concerning reflexes, which—thanks to Sir Charles Sherrington—had lost their definition as inverse, or negative feedback. 3) There was my own confusion of material implication with strict implication. 4) There was my attempt to keep a weather eye open to known so-called field effects when I should have stuck to synaptic transmission proper except for storms like epileptic fits. Finally, 5) there was my ignorance of modulo mathematics that prevented me from understanding regenerative loops and, hence, memory. But neurophysiology moved ahead and, when I went to Chicago I met Walter Pitts, then in his teens, who promptly set me right in matters of theory. It is to him that I am principally indebted for all subsequent success. He remains my best adviser and sharpest critic. You shall never publish this until it passes through his hands. In 1943 he, and I, wrote a paper entitled A Logical Calculus of the Ideas Immanent in Nervous Activity. Thanks to Rashevsky's defense of logical and mathematical ideas in biology, it was published in his journal [Bulletin of Mathematical Biophysics] where, so far as biology is concerned, it might have remained unknown; but John von Neumann picked it up and used it in teaching the theory of computing machines. I will summarize briefly its logical importance. Turing had produced a deductive machine that could compute any computable number, although it had only a finite number of parts which could be in only a finite number of states and although it could only move a finite number of steps forward or backward, look at one spot on its tape at a time and make, or erase, 1 or else 0. What Pitts and I had shown was that neurons that could be excited or inhibited, given a proper net, could extract any configuration of signals in its input. Because the form of the entire argument was strictly logical, and because Godel had arithmetized logic, we had proved, in substance, the equivalence of all general Turing machines—man-made or begotten.
But we had done more than this, thanks to Pitts’ modulo mathematics. In looking into circuits composed of closed paths of neurons wherein signals could reverberate we had set up a theory of memory—to which every other form of memory is but a surrogate requiring reactivation of a trace. Now a memory is a temporal invariant. Given an event at one time, and its regeneration of later dates, one knows that there was an event that was of the given kind. The logician says, “there was some x such that x was a ψ. In the symbols of the principia mathematica, (∃x)(ψx). Given this and negation, for which inhibition suffices, we can have ∼(∃x)(∼ψx), or, if you will, (x)(ψx). Hence we have the lower-predicate calculus with equality, which has recently been proved to be a sufficient logical framework for all of mathematics. Our next joint paper showed that the ψ's were not restricted to temporal invariants but, by reflexes and other devices, could be extended to any universal, and its recognition, by nets of neurons. That was published in Rashevsky's journal in 1947. It is entitled How We Know Universal. Our idea is basically simple and completely general, because any object, or universal, is an invariant under some groups of transformations and, consequently, the net need only compute a sufficient number of averages a., each an Nth of the sum for all transforms T belonging to the group G, of the value assigned by the corresponding functional fi, to every transform T, as a figure of excitation ϕ in the space and time of some mosaic of neurons. That is,
The next difficulty was to cope with the so-called value anomaly. Plato had supposed that there was a common measure of all values. And in the article entitled, A Heterarchy of Values Determined by the Topology of Nervous Nets, (1945) I have shown that a system of six neurons is sufficiently complex to suffer no such “summum bonum.” All of these things you will find summarized in my J.A. Thompson lecture of 2 May 1946, “Finality and Form in Nervous Activity” (shelved by the publisher until 1952), including a prospectus of things to come—all written with Pitts’ help. About this time he had begun to look into the problem of randomly connected nets. And, I assure you, what we proposed were constructions that were proof against minor perturbations of stimuli, thresholds, and connections. Others have published, chiefly by his inspiration, much of less moment on this score, but because we could not make the necessary measurements he has let it lie fallow. Once only did he present it—at an early and unpublished Conference on Cybernetics, sponsored by the Josiah Macy, Jr., Foundation. That was enough to start John von Neumann on a new tack. He published it under the title, Toward a Probabilistic Logic. By this he did not mean a logic in which only the arguments were probable, but a logic in which the function itself was only probable. He had decided for obvious reasons to embody his logic in a net of formal neurons that sometimes misbehaved, and to construct of them a device that was as reliable as was required in modern digital computers. Unfortunately, he made three assumptions, any one of which was sufficient to have precluded a reasonable solution. He was unhappy about it because it required neurons far more reliable than he could expect in human brains. The piquant assumptions were: First, that failures were absolute—not depending upon the strength of signals nor on the thresholds of neurons. Second, that his computing neurons had but two inputs apiece. Third, that each computed the same single Sheffer stroke function. Let me take up these constraints one at a time, beginning with the first alone, namely, when failures are absolute. Working with me, Leo Verbeek, from the Netherlands, has shown that the probability of failure of a neural net can be made as low as the error probability of one neuron (the output neuron) and that this can be reduced by a multiplicity of output neurons in parallel. Second, I have proved that nets of neurons with two inputs to each neuron when failures depend upon perturbations of threshold, stimulus strength or connection—cannot compute any significant function without error—only tautology and contradiction without error. And last, but not least, by insisting on using but a single function, von Neuman had thrown away the great logical redundancy of the system, with which he might have bought reliability. With neurons of 2 inputs each, this amounts to 162; with 3 inputs each, to 2563, etc.—being of the form (22δ)δ where δ is the number of inputs per neuron.
There were two other problems that distressed him. He knew that caffeine and alcohol changed the threshold of all neurons in the same direction so much that every neuron computed some wrong function of its input. Yet one had essentially the same output for the same input. The classic example is the respiratory mechanism, for respiration is preserved under surgical anesthesia where thresholds of all neurons are sky high. Of course, no net of neurons can work when the output neuron's threshold is so high that it cannot be excited or so low that it fires continuously. The first is coma, and the second, convulsion; but between these limits our circuits do work. These circuits he called circuits logically stable under common shift of thresholds. They can be made of formal neurons, even with only two inputs, to work over a single step of threshold, using only excitation and inhibition on the output cell; but this is only a fraction of the range. Associated, unobtrusively, with this problem is this: that of the 16 possible logical functions of neurons with two inputs, two functions cannot be calculated by anyone neuron. They are the exclusion “or,” “A or else B” and “both or else neither”—the “if and only if’ of logic. Both limitations point to a third possibility in the interactions of neurons and both are easily explained if impulses from one source can gate those from another so as to prevent their reaching the output neuron. Two physiological data pointed to the same possibility. The first was described earliest by Matthews, and later by Renshaw. It is the inhibition of a reflex by afferent impulses over an adjacent dorsal root. The second is the direct inhibition described by David Lloyd, wherein there is no time for intervening neurons to get into the sequence of events. We have located this interaction of afferents, measured its strength, and know that strychnine has its convulsive effects by preventing it. This is good physiology, as well as logically desirable.
My collaborator, Manuel Blum, of Venezuela, now has a nice proof that excitation and inhibition on the cell plus inhibitory interaction of afferents are necessary and sufficient for con-structing neurons that will compute their logical functions in any required sequence as the threshold falls or rises. With them it is always possible to construct nets that are logically stable all the way from coma to convulsion under common shift of threshold.
The last of von Neumann's problems was proposed to the American Psychiatry Association in March, 1955. It is this. The eye is only two logical functions deep. Granted that it has controlling signals from the brain to tell it what it has to compute, what sort of elements are neurons that it can compute so many different functions in a depth of 2 neurons (that is, in the bipolars and the ganglion cells). Certainly, said he, neurons are much cleverer than flipflops or the Eccles-Jordan components of our digital computers. The answer to this is that real neurons fill the bill. With formal neurons of 2 inputs each and controlling signals to the first rank only, the output can be made to be any one of 15 of the possible 16 logical functions. Eugene Prange, of the Air Force Cambridge Research Center, has just shown that with neurons of 3 inputs each and controlling signals to all 4 neurons, the net can be made to compute 253 out of 256 possible functions.
IV
Gentlemen, I would not have you think that we are near a full solution of our problems. Jack Cowan, of Edinburgh, has recently joined us and shown that for von Neumann's constructions of reliable circuits we require Post's complete multiple-truth-value logic, for which Boole's calculus is inadequate. Prange has evolved a theory of incomplete mapping that allows us to use “don't-care” conditions as well as assertion and negation. This yields elegant estimations of tolerable segregated errors in circuits with neurons of large numbers of inputs. Captain Robert J. Scott, of the United States Air Force, has begun the computation of minimal nets to sequence the functions computed by neurons as thresholds shift. Many of our friends are building artificial neurons for use in industry and in research, thus exposing to experiment many unsuspected properties of their relations in the time domain. There is now underway a whole tribe of men working on artificial intelligence—machines that induce, or learn—machines that abduce, or make hypotheses. In England alone, there are Ross Ashby, MacKay, Gabor, Andrews, Uttley, Graham Russel, Beurle, and several others—of whom I could not fail to mention Gordon Pask and Stafford Beer. In France, the work centers around Schuetzenberger. The Americans are too numerous to mention.
I may say that there is a whole computing machinery group, followers of Turing, who build the great deductive machines. There is Angyon, the cyberneticist of Hungary, now of California, who had reduced Pavlovian conditioning to a four-bit problem, embodied in his artificial tortoise. Selfridge, of the Lincoln Laboratory, M.I.T.—with his Pandemonium and his Sloppy—is building abductive machinery. Each is but one example of many. We know how to instrument these solutions and to build them in hardware when we will.
But the problem of insight, or intuition, or invention—call it what you will—we do not understand, although many of us are having a go at it. I will not here name names, for most of us will fail miserably and be happily forgotten. Tarski thinks that what we lack is a fertile calculus of relations of more than two relata. I am inclined to agree with him, and if I were now the age I was in 1917, that is the problem I would tackle. Too bad—I'm too old. I may live to see the youngsters do it. But even if we never achieve so great a step ahead of our old schoolmaster we have come far enough to define a number so realistically that a man may know it, and a man so logically that he may know a number. This was all I promised. I have done more, by indicating how he may do it without error, even though his component neurons misbehave.
That process of insight by which a child learns at least one logical particle, neither or not both, when it is given only —and one must be so learned—is still a little beyond us. It may perhaps have to wait for a potent logic of triadic relations, but I now doubt it. This is what we feared lay at the core of the theoretical difficulty in mechanical translation, but last summer Victor Yngve, of the Research Laboratory of Electronics, M.I.T., showed that a small finite machine with a small temporary memory could read and parse English from left to right. In other languages the direction may be reversed, and there may be minor problems that depend on the parenthetical structure of the tongue. But unless the parenthetical structures are, as in mathematics, complicated repeatedly at both ends, the machine can handle even sentences that are infinite—like “This is the house that Jack build.” So I'm hopeful that with the help of Chaos similar simple machines may account for insight or intuition—which is more than I proposed to include in this text. I have done so perhaps not too well but at such speed as to spare some minutes to make perfectly clear to non-Aristotelian logicians that extremely non-Aristotelian logic invented by von Neumann and brought to fruition by me and my coadjutors.
My success arose from the necessity of teaching logic to neurologists, psychiatrists, and psychologist. In his letter to a German princess, Euler used circles on the page to convey inclusions and intersections of classes. This works for three classes. Venn, concerned with four or five, invented his famous diagrams in which closed curves must each bisect all of the areas produced by previous closed curves. This goes well, even for five, by Venn's trick; six is tough; seven, well-nigh unintelligible, even when one finds out how to do it.
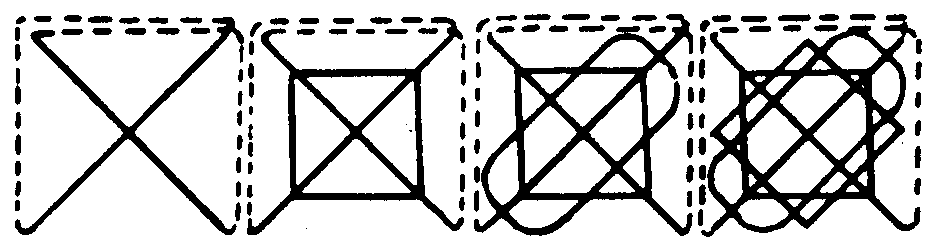
Oliver Selfridge and Marvin Minsky (also of Lincoln laboratory), at my behest, invented a method of construction that can be continued to infinity and remain transparent at a glance. So they formed a simple set of icons wherewith to inspect their contents to the limit of our finite intuitions. The calculus of relations degenerates into the calculus of classes if one is only interested in the one relation of inclusion in classes. This, in turn, degenerates into the calculus of propositions if one is only interested in the class of true, or else false, propositions, or statements in the realistic case. Now this calculus can always be reduced to the relations of propositions by pairs. Thanks to Wittgenstein we habitually handled these relations as truth tables to compute their logical values. These tables, if places are defined, can be reduced to jots for true and blanks for false. Thus, every logical particle, represented by its truth table, can be made to appear as jots and blanks in two intersecting circles.
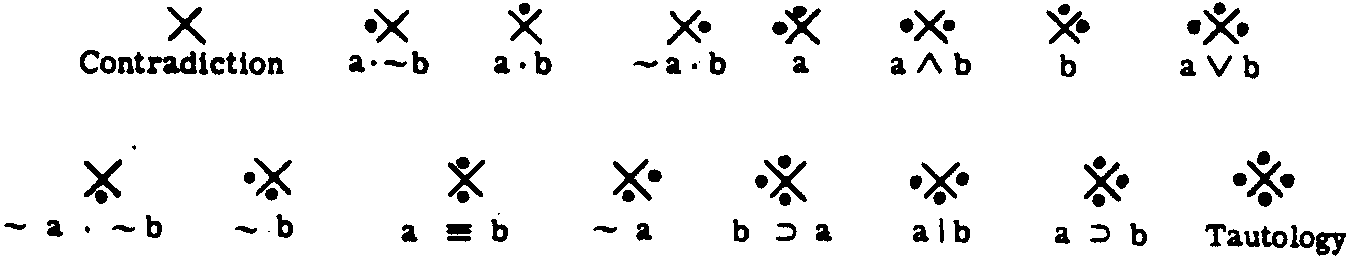
The common area jotted means both; a jot in the left alone means the left argument alone is true; in the right, the right argument alone is true; and below, neither is true. Expediency simplifies two circles to a mere chi or X. Each of the logical relations of two arguments, and there are 16 of them, can then be represented by jots above, below, to right, and to left, beginning with no jots and then with one, two, and three, to end with four. These symbols, which I call Venn functions, can then be used to operate upon each other, exactly as the truth tables do, for they picture these tables.
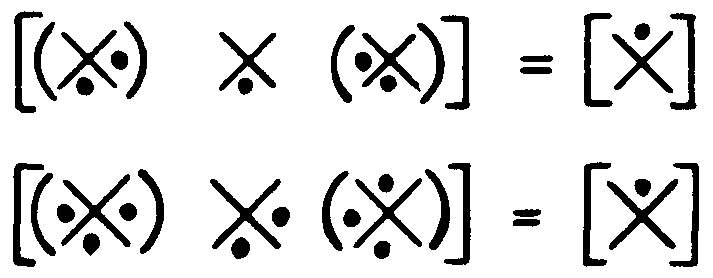
A twelve-year-old boy who is bright learns the laws in a few minutes, and he and his friends start playing jots and X's. A psychiatrist learns them in a few days, but only if he has to pay twenty-five dollars per hour for this psychotherapy. Next, since here we are generating probabilistic logic—not the logic of probabilities—we must infect these functions with the probability of a jot instead of a certain jot or a certain blank. We symbolize this by placing 1 for certain jots, 0 for certain blanks, and p for the probability of a jot in that place. These probabilistic Venn functions operate upon each other as those with jots and blanks, for true and false, utilizing products, instead of only 1x1 = 1 and 1x0 = 0 and 0 x 0 = 0 we get 1, p, p2, p3, 0, etc., and compute the truth tables of our complex propositions. This gives us a truly probabilistic logic, for it is the function, not merely the argument, that is infected by chance and is merely probable. This is the tool with which I attack the problem von Neumann had set us.
A tool is a handy thing—and each has its special purpose. All purpose tools are generally like an icebox with which to drive nails—hopelessly inefficient. But the discovery of a good tool often leads to the invention of others, provided we have insight into the operations to be performed. We have. Logicians may only be interested in tautology—an X with 4 jots—and contradiction—an X with none. But these are tautologically true or false. Realistic logic is interested in significant propositions — that is, in those that are true, or false, according to whether what they assert is, or is not, the case. Nothing but tautology and contradiction can be computed certainly with any p's in every Venn function, so long as one makes them of two and only two arguments. This restriction disappears as soon as one considers Venn functions of more than two arguments in complex propositions. When we have functions of three arguments, Euler's three circles replace the two of conventional logic; but the rules of operations with jots and blanks—or with 1, p, 0—carry over directly, and we have a thoroughly probabilistic logic of three arguments. Then Venn, and Minsky- Selfridge, diagrams enable us to extend these rules to 4, 5, 6, 7, etc. to infinitely many arguments. The rules of calculation remain unaltered, and the whole can be programmed simply into any digital computer. There is nothing in all of this to prevent us from extending the formulations to include multiple-truth-valued logics.
In the Research Laboratory of Electronics we report quarterly progress on our problems. In closing I will read to you my carefully considered statement written nearly a year ago, so that you may hear how one words this for the modern logician working with digital computers, familiar with their logic and the art of programming their activity—for this is now no difficult trick. (I omit only the example and footnote.)
ON PROBABILISTIC LOGIC
[From Quarterly Progress Report, 15 April 1959. Research Laboratory of Electronics, M.I.T.]
Any logical statement of the finite calculus of propositions can be expressed as follows: Subscript the symbol for the δ primitive propositions Aj, with j taking the ascending powers of 2 from 2° to 2δ−-1; written in binary numbers. Thus: A1, A10, A100 and so forth. Construct a V table with spaces S1 subscripted with the integers i, in binary form, from 0 to 2δ-1. Each i is the sum at one and only one selection of j's and so identifies its space as the concurrence of those arguments ranging from S0 for ‘None’ to S2δ-1 for ‘All’. Thus A1 and A100 are in S101 and A10 is not, for which we write A1∈S101 and A100∉S101. In the logical text first replace Aj by Vh with a 1 in S1 if Aj∈Si and with a 0 if Aj∉Si, which makes Vh the truth-table of Aj with T = 1, F = 0. Repeated applications of a single rule serve to reduce symbols for probabilistic functions of any δ Aj to a single table of probabilities, and similarly any uncertain functions of these, etc., to a single Vr with the same subscripts Sr. as the Vh, for the Aj.
This rule reads: Replace the symbol for a function by Vk In which the k of Sk are again the integers in binary form but refer to the h of Vh, and the P'k; of Vk betoken the likelihood of a 1 in Sk. Construct V~r ~and insert in Sr the likelihood P"r of a 1 in Sr computed thus:
Trivial—isn't it?
Gentlemen—you now know what I think a number is that a man may know it and a man that he may know a number, even when his neurons misbehave. I think you will realize that while I have presented you not with a mere logic of probabilities but with a probabilistic logic—a thing which Aristotle never dreamed, yet the whole structure rests solidly on his shoulders—for he is the Atlas who supports the heaven of logic on his Herculean shoulders. In his own words, “Nature will not stand being badly administered.”
Goodby for the Nonce.