AGATHE TYCHE, OF NERVOUS NETS: THE LUCKY RECKONERS [144]
W.S. McCulloch
Introduction
Venn diagrams, with a jot in every space for all cases in which given logical functions are true, picture their truth tables. These symbols serve as arguments in similar expressions that use similar symbols for functions of functions. When jots appear fortuitously with given probabilities or frequencies, the Venn diagram can be written with 1’s for fixed jots, 0’s for fixed absence, and p’s for fortuitous jots. Any function is realizable by many synaptic diagrams of formal neurons of specified threshold, and the fortuitous jots of their symbols can be made to signify a perturbation of threshold in an appropriate synaptic diagram.
Nets of these neurons with common Inputs embody hierarchies of functions, each of which can be reduced to input-output functions pictured in their truth tables. The rules of reduction are simple, even for fortuitous jots, and thus formalize probabilistic logic. Minimal nets of neurons are sufficiently redundant to stabilize the logical input-output function despite common shifts of threshold sufficient to alter the function computed by every neuron, and to assure reliable performance of nets of unreliable neurons. Both types of nets are flexible as to the functions they can compute when controlled by imposed changes of threshold.
The neurons, the variations of their thresholds, their excitations and inhibitions are realistic; and there remains sufficient redundancy for statistical control of growth to produce the synapsis of these stable, reliable and flexible nets.
NEUROPHYSIOLOGISTS are indebted to John von Neumann for his studies of components and connections in accounting for the steadiness and the flexibility of behavior. In speaking to the American Psychiatric Association (1) he stressed the utility and the inadequacy of known mechanisms for stabilizing nervous activity, namely, (a) the threshold of nonlinear components, (b) the negative feedback of reflexive mechanisms, (c) the internal switching to counteract changes - “ultrastablllty” (2) - , and (d) the redundancy of code and or channel. He suggested that the flexibility might depend upon local shifts of thresholds or incoming signals to components that are more appropriate to computers than any yet invented. His Theory of Games (3) has initiated studies that may disclose several kinds of stability and has indicated where to look for logical stability under common shift of threshold. His “Toward a Probabilistic Logic” (4) states the problem of securing reliable performance from unreliable components, but his solution requires better relays than he could expect in brains. These, his interests, put the questions we propose to answer. His satisfaction with our mechanisms for realizing existential and universal quantification in nets of relays (5, 6) limits our task to the finite calculus of propositions. Its performance has been facilitated by avoiding the opacity of the familiar symbols of logic and the misleading suggestions of multiplication and addition modulo two of the facile Boolean notation for an algebra that is really substitutive, (7, 8, 9). Our symbols have proved useful In teaching symbolic logic In psychological and neurological contexts (10). Familiarity with them undoubtedly contributed to the invention of the circuits whose redundancy permits solution of our problems.
The finite calculus of propositions can be written at great length by repetitions of a stroke signifying the incompatibility of Its two arguments, the traditional five symbols, ‘∼’ for ‘not’; ‘⋅’ for ‘both’; ‘V’ for ‘or’; ‘⊃’ for ‘implies’; and ’≡’ for ‘if and only if’, shorten the text but require conventions and rearrangements in order to avoid ambiguities. Economy requires one symbol for each of the sixteen logical functions of two propositions. The only necessary convention is then one of position or punctuation.
Since the logical probability and the truth value of a propositional function are determined by its truth table, each symbol should picture its table. When the place in the table is given, any jot serves for “true” and a blank for “false”. When the four places in the binary table are indicated by ’×’ it is convenient to let the place to the left show that the first proposition alone is the case; to the right, the second; above, both; and below, neither. Every function is then pictured by jots for all of those cases in which the function is true. Thus we write 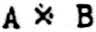 for contradiction;
for contradiction; 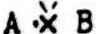 for A · ∼ B;
for A · ∼ B;  for A · B;
for A · B; 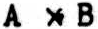 for B · ∼ A;
for B · ∼ A; 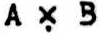 for ∼ A · ∼ B;
for ∼ A · ∼ B;  for A · (Bv ∼ B);
for A · (Bv ∼ B); 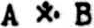 for (Av ∼ A) · B;
for (Av ∼ A) · B;  for ∼ A · (Bv ∼ B);
for ∼ A · (Bv ∼ B); 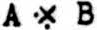 for (AV ∼ A) · ∼ B;
for (AV ∼ A) · ∼ B;  for (A · ∼ B) v (∼ A · B);
for (A · ∼ B) v (∼ A · B);  for A ≡ B;
for A ≡ B; 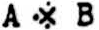 for B ⊃ A;
for B ⊃ A;  for A v B;
for A v B; 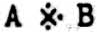 for A ⊃ B;
for A ⊃ B; 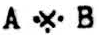 for ∼(A · B); and
for ∼(A · B); and 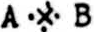 for tautology. The × or chi, may be regarded as an elliptical form of Venn’s diagram for the classes of events of which the propositions A and B are severally and jointly true and false; for in fig. 1, the chi remains when the dotted lines are emitted. Similar symbols can therefore be made from Venn symbols, for functions of more than two arguments. Each additional line must divide every pre-existing area into two parts. Hence, for the number of arguments δ there are 2δ spaces for jots and 22δ symbols for functions. (See Fig. 1.)
for tautology. The × or chi, may be regarded as an elliptical form of Venn’s diagram for the classes of events of which the propositions A and B are severally and jointly true and false; for in fig. 1, the chi remains when the dotted lines are emitted. Similar symbols can therefore be made from Venn symbols, for functions of more than two arguments. Each additional line must divide every pre-existing area into two parts. Hence, for the number of arguments δ there are 2δ spaces for jots and 22δ symbols for functions. (See Fig. 1.)
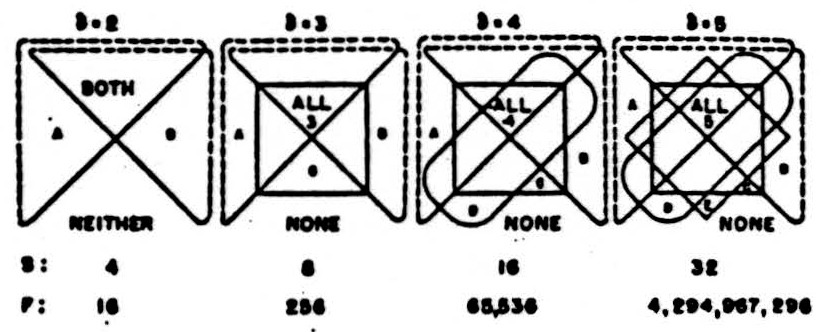
Figure 1. Venn figures with spaces for all intersections of δ classes. S is the number of spaces; F, the number of functions.
Formulas composed of our chiastan symbols are transparent when the first proposition Is represented by a letter to the left of the × and the second to the right. When these spaces are occupied by expressions for logical variables, the formula is that or a propositional function; when they are occupied by expressions for propositions, of a proposition; consequently the formula can occupy the position of an argument in another formula.
Two distinct propositions, A and B, are independent when the truth value of either does not logically affect the truth value of the other. A formula with only one × whose spaces are occupied by expressions for two independent propositions can never have an × with no jots or four jots. The truth value of any other proposition is contingent upon the truth values of its arguments. Let us call such a proposition “a significant proposition of the first rank.”
A formula of the second rank is made by inserting into the spaces for the arguments of its × two formulas of the first rank; for example, 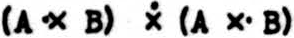 . When the two propositions of the first rank are composed of the same pair of propositions in the same order, the resulting formula of the second rank can always be equated to a formula of the first rank by putting jots into the × for the corresponding formula of the first rank according to the following rules of reduction:
. When the two propositions of the first rank are composed of the same pair of propositions in the same order, the resulting formula of the second rank can always be equated to a formula of the first rank by putting jots into the × for the corresponding formula of the first rank according to the following rules of reduction:
write the equation in the form (…x1…) x2 (…x3…) = (…x4…); wherein the xj are chiastan symbols:
If x2 has a jot on its left, put a jot into x4 in every space where there is a jot in x1 and no corresponding jot in x3. Thus,
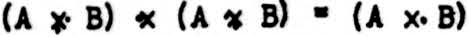
If x2 has a jot on its right, put a jot into x4 in every space where there is a jot in x3 and no corresponding jot in x1. Thus,
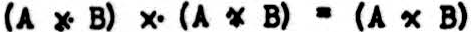
If x2 has a jot above, put a jot into x4 in every space where there is a jot in both x1 and x3. Thus,
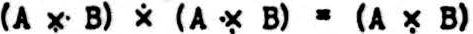
If x2 has a jot below, put a jot into x4 in every space that is empty in both x1 and x3. Thus,
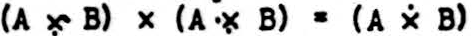
If there is more than one jot in x2 apply the foregoing rules seriatim until all jots on x2 have been used. Put no other jots into x4.
By repetition of the construction we can produce formulas for functions of the third and higher ranks and reduce them step by step to the first rank, thus discovering their truth values.
Since no other formulas are used In this article, the letters A and B are omitted, and positions, left and right, replace parentheses.
In formulas of the first rank the chance addition or omission of a jot produces an erroneous formula and will cause an error only in that case for which the jot is added or omitted, which is one out of the four logically equiprobable cases. With the symbols proposed for functions of three arguments, the error will occur in only one of the eight cases, and, in general, for functions of δ arguments. In one of 2δ cases. If Pδ is the probability of the erroneous jot and P the probability of error produced, P = 2δ p. In empirical examples the relative frequency of the case In question as a matter of fact replaces the logical probability.
In formulas for the second rank there are three ×’s. If we relax the requirement of independence of the arguments, A and B, there are then 163 possible formulas each of which reduces to a formula of the first rank. Thus the redundancy, R, of these formulas of the second rank is 163/16 = 162. For functions of δ arguments. R = (22δ)δ.
To exploit this redundancy so as to increase the reliability of inferences from unreliable symbols, let us realize the formulas in nets of what von Neumann called neurons (3). Each formal neuron is a relay which on receipt of all-or-none signals either emits an all-or-none signal or else does not emit one which it would otherwise have emitted. Signals approaching a neuron from two sources either do not interact, or, as we have shown,(11, 12) those from one source prevent some or all of those from the other source from reaching the recipient neuron. The diagrams of the nets of fig. 2 are merely suggested by the anatomy of the nervous system. They are to be interpreted as follows.
A line terminating upon a neuron shows that it excites it with a value +1 for each termination. A line forming a loop at the top of the neuron shows that it Inhibits it with a value or excitation or -1 for each loop. A line forming a loop around a line approaching a neuron shows that it prevents excitation or inhibition from reaching the neuron through that line.
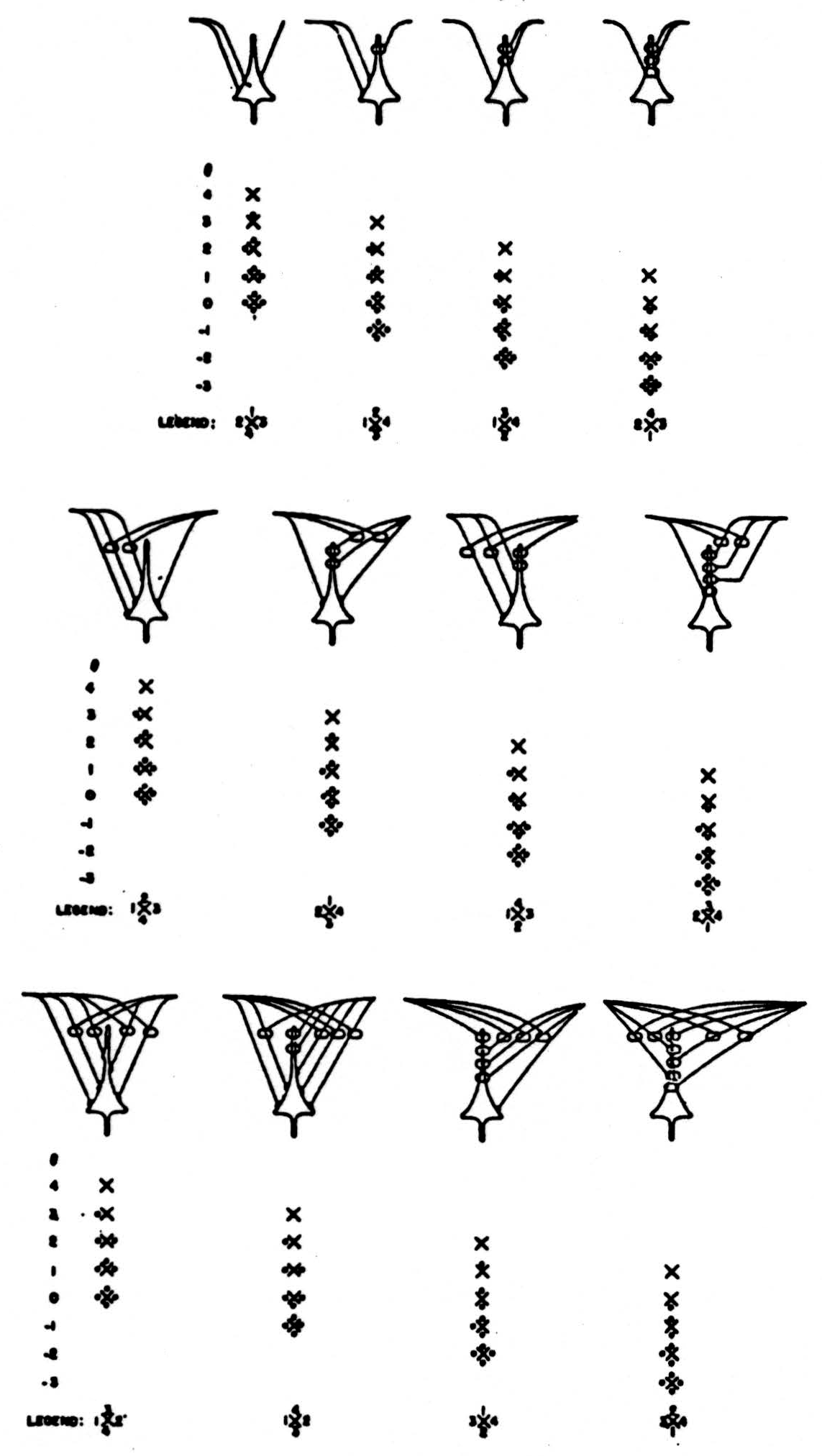
Figure 2. Synaptic diagrams for  appearing before
appearing before  .
.
Each neuron has on any occasion a threshold, θ, measured in steps of excitation, and it emits a signal when the excitation it receives is equal to or greater than θ. The output of the neuron is thus some function of its input, and which function it is depends upon both its local connections and the threshold of the neuron, these functions can be symbolized by ×’s and jots beginning with none and adding one at a time as θ decreases until all four have appeared in the sequence noted in the legend for its diagram in fig. 2. These are the simplest diagrams fulfilling the requirement. All simpler diagrams are degenerate, since they either fail to add one jot or else add more than one jot for some step in θ. Because all 24 sequences (of which only 12 left-handed are drawn) are thus realized, we can interpret the accidental gain or loss of a jot or jots in an intended × as a change on the threshold of an appropriate neuron.
Any formula of the second rank Is realized by a net of three neurons each of whose thresholds is specified; for example, see fig. 3. The formula can be reduced to one of the first rank whose × pictures the relation of the output of the net to the input of the net.
When all thresholds shift up or down together, so that each neuron is represented by one more, or one less, jot in its × but the reduced formula is unaltered, the net is called “logically stable.”
The redundancy of formulas of the second rank provides us with many examples or pairs of formulas and even triples of formulas that reduce to the same formula of the first rank and that can be made from one another by common addition or omission of one jot in each ×, and the diagrams of fig. 2 enable us to realize them all in several ways: For example, there are 32 triples of formulas and 64 logically stable nets for every reduced formula with a single jot. Even nets of degenerate diagrams enjoy some logical stability; for example  goes to
goes to  .
.
If such nets are embodied in our brains they answer von Neumann’s repeated question of how it is possible to think and to speak correctly after taking enough absinthe or alcohol to alter the threshold of every neuron. The limits are clearly convulsion and coma, for no formula is significant or its net stable under a shift of θ that compels the output neuron to compute tautology or contradiction. The net of fig. 3 is logically stable over the whole range between these limits. Let the causes and probabilities of such shifts be what they may, those that occur simultaneously throughout these nets create no errors.
Logically stable nets differ greatly from one another in the number of errors they produce when thresholds shift independently in their neurons and the most reliable make some errors; for example, the net of fig. 4.

Figure 3. A logically stable net for 
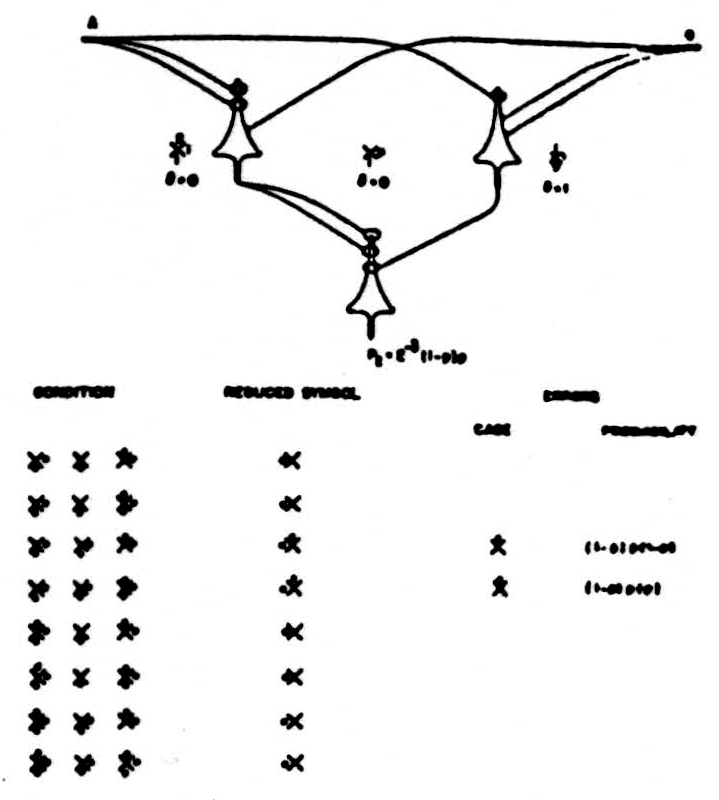
Figure 4. A best stable net for 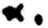
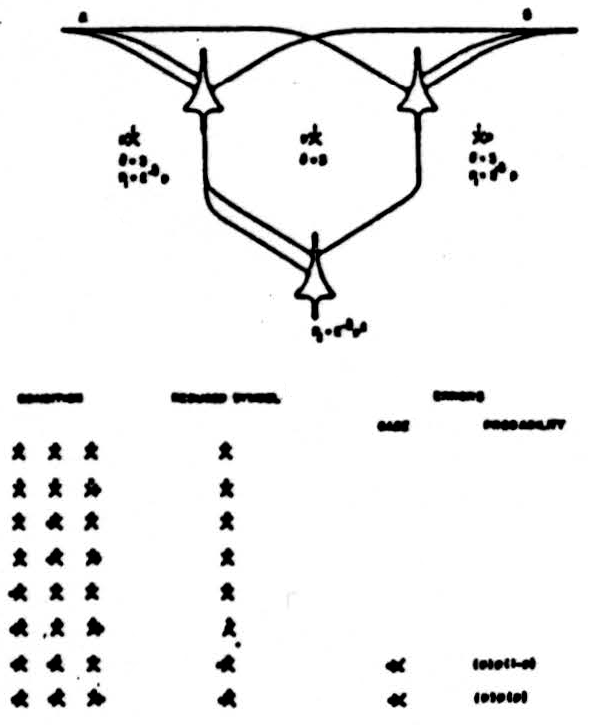
Figure 5. A best unstable net for 
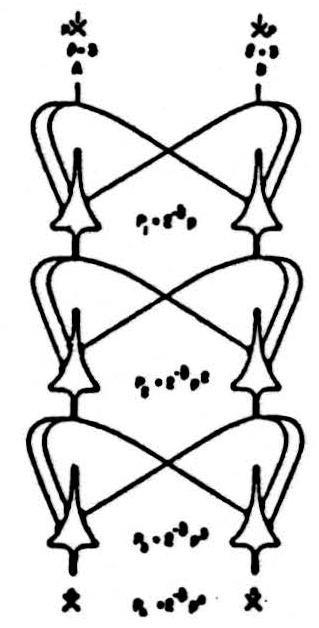
Figure 6. Unstable improvement net for  .
.
To Include Independent shifts, let our chiastan symbols be modified by replacing a jot with 1 when the jot is never omitted and with p when that jot occurs with a probability p, and examine the errors extensively as in fig. 4. Here we see that the frequency of the erroneous formulas is p(1−p), and the actual error is a deficit of a jot at the left in the reduced formula in each faulty state of the net, i,e., in one case each. Hence we may write for the best of stable nets P2 ≠ 2-2 p(1−p). The factors p and (1−p) are to be expected in the errors produced by any net which is logically stable, for the errors are zero when p = 0 or p = 1. No stable net is more reliable.
No designer of a computing machine would specify a neuron that was wrong more than half of the time; for he would regard it as some other neuron wrong less than half of the time; but in these more useful of logically stable circuits, it makes no difference which way he regards it, for they are symmetrical in p and 1 − p. At p = 1/2, the frequency of error is maximal and is P2 = 2-2 1/2(1 − 1/2) = 1/16, which is twice as reliable as its component neurons for which P1= 2-2 1/2 = 1/8.
Among logically unstable circuits the most reliable can be constructed to secure fewer errors than the stable whenever p < 1/2. The best are like that of fig. 5. The errors here are concentrated In the two least frequent states and in only one of the four cases. Hence P2 = 2-2 p2.
Further improvement requires the construction of nets to repeat the improvement of the first net and, for economy, the number of neurons should be a minimum. For functions of δ arguments each neuron has inputs from δ neurons. Hence the width of any rank is δ, except the last, or output, neuron. If n be the number of ranks, then the number of neurons, N, is δ(n−1) + 1.
Figure 6 shows how to construct one of the best possible nets for the unstable ways of securing improvement with two output neurons as inputs for the next rank. The formulas are selected to exclude common errors in the output neurons on any occasion. In these, the best of unstable nets, the errors of the output neurons are Pn = 2-δpn.
[Whether we are Interested in shifts of threshold or in noisy signals, it is proper to ask what improvement is to be expected when two or three extra jots appear in the symbols. With our nondegenerate diagrams for neurons a second extra jot appears only if the first has appeared, and a third only if the second. If the probability p of an extra jot is kept constant, the probability of two extra jots is p2 and of three is p3. Examination of the net in fig. 6 shows that P2 < P1, If p + p2 + p3 < 0.15 or p < 0.13. To match Gaussian noise the log of successive p’s should decrease as (Δθ)2, or 1, p, p4, p9 giving P2 < P1 for p < 0.25. The remaining errors are always so scattered as to preclude further improvement in any subsequent rank.]
When common shifts of θ are to be expected, or all we know is 0 < p < 1, a greater improvement is obtained by alternating stable and unstable nets as in fig. 7, selected to exclude common errors in its output neurons. For n even Pn = 2−δ pn/2 (1−p)n/2 and the expected error is
which is less than with any other compositions of δ = 2 nondegenerate diagrams.
When δ = 3, the redundancy,
There are

Figure 7. Alternating improvement net for ẋ.
None of these nets increases reliability in successive ranks under von Neumann's condition that neurons fire or fall with probability p regardless of input; but they are more interesting neurons. They are also more realistic. In the best controlled experiments the record of a single unit, be it cell body or axon, always indicates firing and falling to fire at near threshold values of constant excitation, whether it is excited transynaptically or by current locally applied. At present, we do not know how much of the observed flutter of threshold is due to activity of other afferent impulses and how much is intrinsic fluctuation at the trigger point. We have not yet a reasonable guess as to its magnitude in neurons in situ, and for excised nerve we have only two estimates of the range: one, about 2 per cent; and the other, 7 per cent (14, 15). Our own measurements on a single node of Ranvier would indicate a range of 10 per cent. To discover regularities of nervous activity we have naturally avoided stimulation near threshold. Now we must measure the intrinsic jitter, for this determines both the necessity or improving circuits and the maximum number of afferent terminals that can be discriminated. Eventually we will have to take into account the temporal course of excitation and previous response, for every impulse leaves a wake of changing threshold along its course.
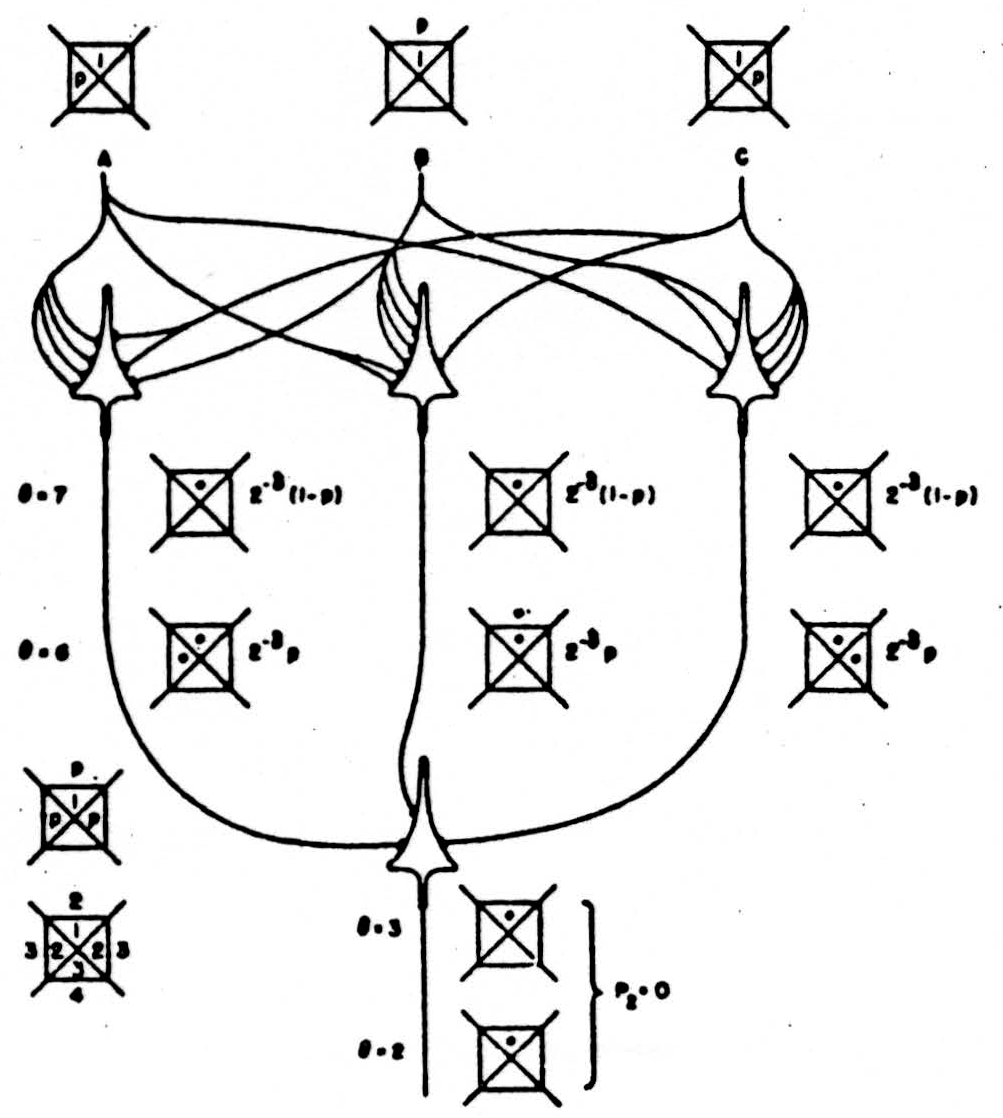
Figure 8. Input δ = 3, output degenerate δ = 3 neuron for ẋ.
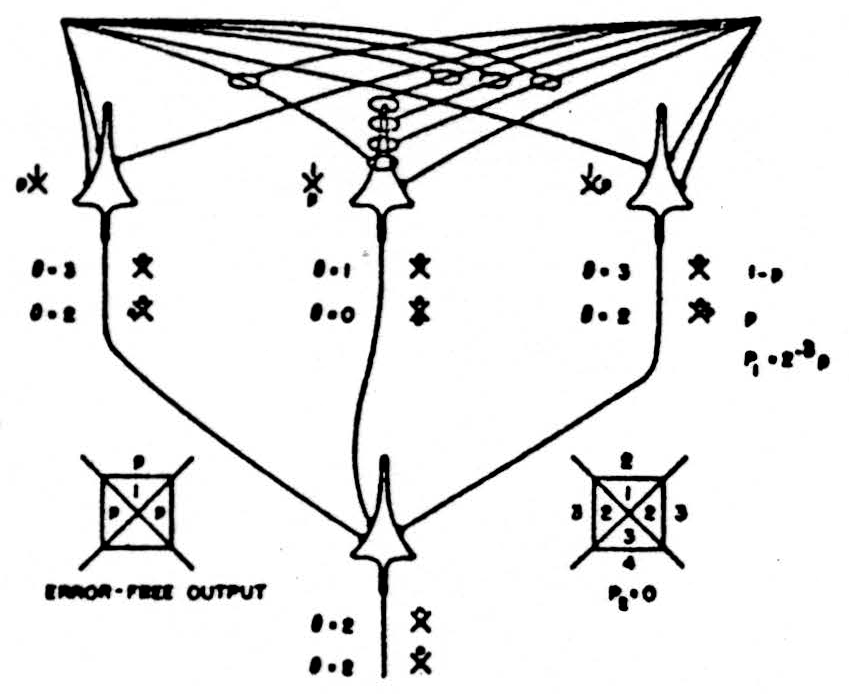
Figure 9. Input δ = 2, output degenerate δ = 3 neuron for  .
.

Figure 10. Flexible net, always unstable.
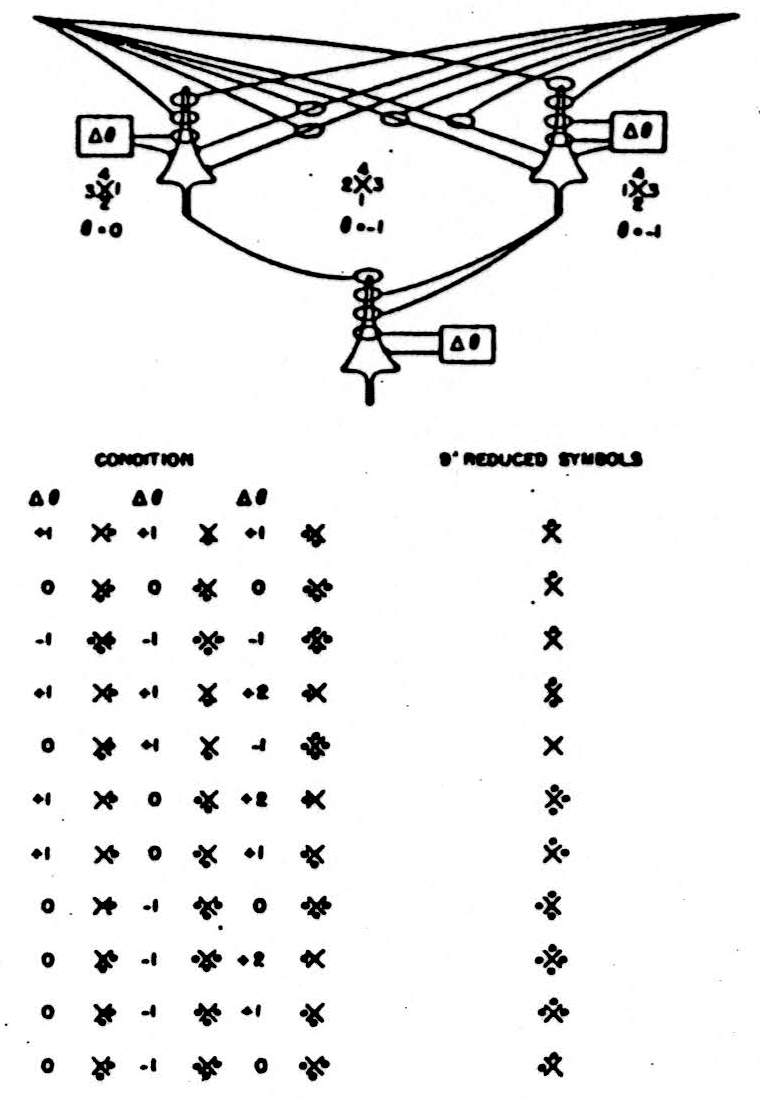
Figure 11. Flexible net, logically stable for ẋ.
Despite the increase in reliability of a net for a function of the second rank some of these nets can be made to compute as many as 14 of the 16 reduced formulas by altering the thresholds of the neurons by means of signals from other parts of the net, as in fig. 10. and even some logically stable nets for triples of formulas can be made to realize 9 of the 16, as in fig. 11. Even this does not exhaust the redundancy of these nets, for both of them can be made to compute many of these functions in several ways.
The diagrams of fig. 2 were drawn to ensure a change in function for every step in θ. Actual neurons have more redundant connexions. We are examining how to use this redundancy to design reliable nets the details of whose connexions are subject to statistical constraints alone. This is important because our genes cannot carry enough information to specify synapsis precisely.
For the moment, it is enough that these appropriate, formal neurons have demonstrated logical stability under common shift of threshold and have secured reliable performance by nets of unreliable components without loss of flexibility.
Footnote
This work was supported in part by Bell Telephone Laboratories, Incorporated; in part by The Teagle Foundation, Incorporated, and in part by National Science Foundation.
References
NEUMANN, J. von. Fixed and random logical patterns and the problem of reliability. American Psychiatric Association, Atlantic City, May 12. (1955).
ASHBY, W. ROSS, Design Tor a Brain, John Wiley and Sons, Inc., New York. (1952).
NEUMAN, J. von. and MORGENSTERN, O. Theory of Games and Economic Behaviour. Princeton University Press, Princeton, N.J. (1944).
NEUMANN, J. von. Probabilistic Logics and the synthesis of Reliable Organisms from Unreliable Components. Automata Studies, edited by C. E. Shannon and J. McCarthy. Princeton University Press, Princeton, N.J. (1956).
McCULLOCH, W. S. and PITTS. W. A logical calculus of the Ideas immanent In nervous activity. Bull.. Maths, and Biophys., 1943, 5, 115.
PITTS, W. and McCULLOCH, W. S. How we know universals. The perception of auditory and visual forms. Bull. Maths. and Biophys., 1947 , 9, 127.
MENGER. K. Algebra of Analysis, Notre Dame Mathematical Lectures, No.3. University of Notre Dame, Notre Dame, Ind. (1944).
MENGER, K. Analysis without variables. J. Symbol. Logic, 1946, I, 30.
MENGER, K. General algebra of analysis. Reports of a Mathematical Colloquium, Series 2, issue 7. (1946).
McCULLOCH, W. S. Machines that know and want. Brain and Behaviour, A Symposium, edited by W. C. Halstead; Comparative Psychology Monographs 20, No. 1, University of California Press, Berkeley and Los Angeles. (1950).
McCULLOCH, W. S., HOWLAND, B., LETTVIN, J. Y.. PITTS, W. and WALL, P. D. Reflex inhibition by dorsal root interaction. J. Neurophysiol., 1955, 18, 1.
McCULLOCH, W. S., WALL, P. D., LETTVIN, J. Y. and PITTS, W. H. Factors limiting the maximum impulse transmitting ability of an afferent system of nerve fibers. Information Theory, Third London Symposium, edited by C. Cherry. Academic Press, Inc., New York. (1956).
McCULLOCH, W. S. Quarterly Progress Report of the Research Laboratory of Electronics, M.I.T. (Neurophysiology), October 1957.
BLAIR, E. A. and ERLANGER, J. A, A comparison of the characteristics of axons through their individual electrical responses. Am. J. Phys., 1933, 106, 524. ’
PECHER, C. La fluctuation d’excitabilité de la fibre nerveuse. Arch. Internat. de Physiol., 1939, 49, 129.