Complexity and Life
Fritjof Capra
Center for Ecoliteracy, USA
Introduction
Let me begin by discussing some dramatic recent developments in our understanding of the nature of life (see Capra, 2002). Over the past ten years, molecular biologists have been engaged in one of the most ambitious projects in modern science, the attempt to identify and map the complete genetic sequence of the human species, which contains tens of thousands of genes.
As you know, the first stage of the Human Genome Project was successfully completed about a year ago. The results of this tremendous achievement, together with the successful mappings of other genomes, have triggered a conceptual revolution in genetics that is likely to change our understanding of life radically (see Fox Keller, 2000; Capra, 2002: 142ff). To appreciate these changes, let me briefly review the history of the modern scientific concept of life.
In 1944, the Austrian physicist Erwin Schrödinger wrote a short book titled What is Life?, in which he advanced clear and compelling hypotheses about the molecular structure of genes. This book stimulated biologists to think about genetics in a novel way and opened a new frontier of science, molecular biology.
During subsequent decades, this new field generated a series of triumphant discoveries, culminating in that of the DNA double helix and the unraveling of the genetic code. For several decades after these discoveries, biologists believed that the “secret of life” lay in the sequences of genetic elements along the DNA strands. If we could only identify and decode those sequences, so the thinking went, we would understand the genetic “programs” that determine all biological structures and processes. This view of life, known as “genetic determinism,” is now being seriously challenged.
The newly developed sophisticated techniques of DNA sequencing and of related genetic research increasingly show that the traditional concept of a genetic program, and maybe even the concept of the gene itself, are in need of radical revision. And so more and more biologists are looking for a different answer to Schrödinger's old question, “What is Life?”
The conceptual revolution that is now taking place in biology is a profound shift of emphasis from the structure of genetic sequences to the organization of metabolic networks. It is a shift from reductionist to systemic thinking. The issue, simply stated, is this: To understand the nature of life, it is not enough to understand DNA, proteins, and the other molecular structures that are the building blocks of living organisms, because these structures also exist in dead organisms, for example in a dead piece of wood or bone.
The difference between a living organism and a dead organism lies in the basic process of life—in what sages and poets throughout the ages have called the “breath of life.” In modern scientific language, this process of life is called “metabolism.” It is the ceaseless flow of energy and matter through a network of chemical reactions, which enables a living organism continually to generate, repair, and perpetuate itself.
METABOLISM AND THE EPIGENETIC NETWORK
The understanding of metabolism includes two basic aspects. One is the continuous flow of energy and matter. Living systems are open systems. They continually take in food and produce waste. In other words, a living system operates far from equilibrium. Matter continually flows through it, and yet the system maintains a stable form.
To visualize this nonequilibrium state, think of a vortex, for example a whirlpool in a bathtub. Water continually flows through the vortex, yet its characteristic shape remains stable. Metaphorically, we can visualize a living organism as a whirlpool, that is, as a stable structure with matter and energy continually flowing through it.
The second aspect of metabolism is the metabolic network, a network of chemical reactions that breaks down the food and uses the nutrients to grow the organism's biological structures. One of the most important insights of the new understanding of living systems is the recognition that networks are the basic pattern of life. Ecosystems are understood in terms of food webs (networks of organisms); organisms are networks of cells, organs, and organ systems; and cells are networks of molecules. The network is a pattern that is common to all life. Wherever we see life, we see networks.
The first key characteristic of these living networks is that they create their own boundary. A cell, for example, is enclosed by the cell membrane that discriminates between the system—the “self,” as it were—and its environment. The membrane is semipermeable, keeping certain substances out and letting others in, and in this way it regulates the cell's molecular composition and preserves its identity. These semipermeable membranes are a universal characteristic of cellular life.
The second key characteristic of living networks is that they are self-generating. In a cell, all the biological structures—the proteins, enzymes, DNA, cell membrane, and so on—are continually produced, repaired, and regenerated by the cellular network. Similarly, at the level of a multicellular organism, the bodily cells are continually regenerated and recycled by the organism's metabolic network.
When we try to describe the metabolic network of a cell in detail, we see immediately that it is very complex, even for the simplest bacteria. Most metabolic processes are catalyzed by enzymes and receive energy through special phosphate molecules known as ATP. The enzymes alone form an intricate network of catalytic reactions, and the ATP molecules form a corresponding energy network. Through the messenger RNA, both of these networks are linked to the genome, itself a complex interconnected web, in which genes directly and indirectly regulate one another's activity. In other words, the metabolic network includes the genetic level but extends to levels beyond the genes. It is therefore also known as the “epigenetic” network.
The recent advances in genetics have shown that this epigenetic network plays a critical role in all biological processes involving genes. The fidelity of DNA replication, the rate of mutations, the transcription of coding sequences, the selection of protein functions, and the patterns of gene expression are all regulated by the epigenetic network in which the genome is embedded. This network is highly nonlinear, containing multiple feedback loops, so that patterns of genetic activity continually change in response to changing circumstances.
Let me now summarize my description of metabolism by identifying four key characteristics of biological life (see Capra, 2002: 13):
- A living system is materially and energetically open; it needs to take in food and excrete waste to stay alive.
- It operates far from equilibrium; there is a continual flow of energy and matter through the system.
- It is organizationally closed, a metabolic network bounded by a membrane.
- It is self-generating; each component helps to transform and replace other components.
NONLINEARITY
These four characteristics all have one thing in common: They are characteristics of a system whose dynamics and pattern of organization are nonlinear. Nonequilibrium systems are nonlinear systems; networks are nonlinear patterns of organization. This is where complexity theory comes in. It is so important for understanding living systems, because it is a nonlinear mathematical theory. Indeed, its technical name is “nonlinear dynamics.”
In science, until recently, we always avoided the study of nonlinear systems, because the mathematical equations describing them are very difficult to solve. Whenever nonlinear equations appeared they were immediately “linearized,” that is, replaced by linear approximations. Instead of describing the phenomena in their full complexity, the equations of classical science deal with small oscillations, shallow waves, small changes of temperature, and so on, for which linear equations can be formulated. This became such a habit that most scientists and engineers came to believe that virtually all natural phenomena could be described by linear equations.
The decisive change over the last three decades has been to recognize the importance of nonlinear phenomena, and to develop mathematical techniques for solving nonlinear equations. The use of computers has played a crucial role in this development. With the help of powerful, high-speed computers, mathematicians are now able to solve complex equations that had previously been intractable.
In doing so they have devised a number of techniques, a new kind of mathematical language that revealed very surprising patterns underneath the seemingly chaotic behavior of nonlinear systems, an underlying order beneath the apparent chaos. Indeed, chaos theory, an important branch of nonlinear dynamics, is really a theory of order, but of a new kind of order that is revealed by this new mathematics.
PHASE SPACE AND ATTRACTORS
Let me now review some of the main features of nonlinear dynamics, the theory of complexity (see Capra, 1996: 112ff). When you solve a nonlinear equation with these new mathematical techniques, the result is not a formula but a visual shape, a pattern traced by the computer known as an “attractor.” The mathematics of complexity is essentially a mathematics of patterns.

Figure 1 The Ueda attractor
To illustrate this, let me show you a typical example, known as the “chaotic pendulum,” which was studied first by the Japanese mathematician Ueda in the late 1970s. It is a nonlinear electronic circuit with an external drive, which is relatively simple but produces extraordinarily complex behavior. Each swing of this chaotic oscillator is unique; the system never repeats itself. However, in spite of the seemingly erratic motion, the attractor representing the system's complex dynamics is simple and elegant. It is now known as the Ueda attractor (see Figure 1). As you can see, it generates patterns that almost repeat themselves, but not quite. This is a typical feature of the so-called strange attractors of chaotic systems.
Let's take a closer look at this attractor. It is a pattern in two dimensions, defined by the two variables needed to describe a pendulum: its position (or angle) and its velocity. These two variables define a mathematical space called “phase space.” Each point in the space is determined by the values of the system's two variables, which in turn completely determine the state of the system.
In other words, each point in phase space represents the system in a particular state. As the pendulum moves, the point representing it traces out a trajectory that represents the dynamics of the system. The attractor is the pattern of this trajectory in phase space. It is called an “attractor” because it represents the system's long-term dynamics. A nonlinear system will typically move differently in the beginning, depending on how you start it off, but then will settle down to a characteristic long-term behavior, represented by an attractor. Metaphorically speaking, the trajectory is “attracted” to this pattern whatever its starting point may have been.
It is important to realize that this trajectory in phase space is not the physical trajectory of the chaotic pendulum. It is a visual representation of the pendulum's complex dynamics in an abstract mathematical space. In this case, the phase space has two dimensions, because the system is determined by only two variables. For more complex systems, the phase space will have more than two dimensions, one for each variable of the system.
FRACTAL GEOMETRY
When we magnify the picture of the Ueda attractor, we discover a multilayered substructure in which the same patterns are repeated again and again. This property of similar geometric patterns appearing repeatedly at different scales is known as “self-similarity” and is the defining characteristic of fractal geometry, which is another important branch of nonlinear dynamics.
Fractal geometry was originally developed by Benoît Mandelbrot to study the geometry of a wide variety of irregular natural phenomena, and it was only later that its connection with chaos theory was discovered. Since then it has become customary to define strange attractors as trajectories that exhibit fractal geometry.
Over the past 20 years scientists and mathematicians have explored a wide variety of complex systems. In case after case they would set up nonlinear equations and have computers trace out the solutions as trajectories in phase space. To their great surprise, these researchers discovered that there is a very limited number of different attractors. Their shapes can be classified topologically, and the general dynamic properties of a system can be deduced from the shape of its attractor.
SIMPLICITY AND COMPLEXITY
The exploration of nonlinear systems over the past decades has had a profound impact on science as a whole, as it has forced us to re-evaluate some very basic notions about the relationships between a mathematical model and the phenomena it describes. One of those notions concerns our understanding of simplicity and complexity.

Figure 2 The Mandelbrot set
In the world of linear equations we thought we knew that systems described by simple equations behaved in simple ways, while those described by complicated equations behaved in complicated ways. In the nonlinear world—which includes most of the real world, as we begin to discover—simple deterministic equations may produce an unsuspected richness and variety of behavior. One of the most fascinating examples is the now well-known Mandelbrot set (Figure 2), a fractal structure that displays a richness defying the human imagination and that yet can be generated with a very simple iterative procedure.
On the other hand, complex and seemingly chaotic behavior can give rise to ordered structures, to subtle and beautiful patterns. Indeed, the term “chaos” has acquired a new technical meaning. The behavior of chaotic systems is not merely random but shows a deeper level of patterned order.
A central feature of nonlinear systems is the frequent occurrence of self-reinforcing feedback processes. This has several surprising consequences. In linear systems, small changes produce small effects, and large effects are due either to large changes or to a sum of many small changes. In nonlinear systems, by contrast, small changes may have dramatic effects because they may be amplified by repeated feedback.
FROM QUANTITY TO QUALITY
Because of the possibility that small differences may be amplified by repeated feedback, nonlinear systems are extremely sensitive to their initial conditions. Minute changes in the system's initial state will lead over time to large-scale consequences. In chaos theory this is known as the “butterfly effect” because of the half-joking assertion that a butterfly stirring the air today in Beijing can cause a storm in New York next month.
The butterfly effect was discovered in the early 1960s by the meteorologist Edward Lorenz, who designed a very simple model of weather conditions consisting of three coupled nonlinear equations. He found that the solutions to his equations were extremely sensitive to the initial conditions. From virtually the same starting point, two trajectories would develop in completely different ways, making any long-range prediction impossible.
This discovery sent shock waves through the scientific community, which was used to relying on deterministic equations for predicting phenomena such as solar eclipses or the appearance of comets with great precision over long spans of time. It seemed inconceivable that strictly deterministic equations of motion should lead to unpredictable results. Yet this was exactly what Lorenz had discovered.
Mathematically, this means that we can never predict at which point in phase space the trajectory of a chaotic system will be at a certain time, even though the system is governed by deterministic equations. The point is that, in order to calculate the trajectory's evolution, we always need to round off the calculation after a certain number of decimal places, even with the most powerful computers; and after a sufficient number of iterations, or feedback loops, even the most minimal round-off errors will have added up to enough uncertainty to make predictions impossible.
The impossibility of predicting at which point in phase space the trajectory of a chaotic attractor will be at a certain time does not mean that chaos theory is not capable of any predictions. We can still make very accurate predictions, but they concern the qualitative features of the system's behavior rather than the precise values of its variables at a particular time. Nonlinear dynamics thus represents a shift from quantity to quality. Whereas conventional mathematics deals with quantities and formulas, complexity theory deals with quality and pattern.
Indeed, the analysis of nonlinear systems in terms of the topological features of their attractors is known as “qualitative analysis.” A nonlinear system can have several attractors and they may be of several different types. All trajectories starting within a certain region of phase space will lead sooner or later to the same attractor. This region is called the “basin of attraction” of that attractor. Thus the phase space of a nonlinear system is partitioned into several basins of attraction, each embedding its separate attractor.
The qualitative analysis of a dynamic system consists in identifying the system's attractors and basins of attraction, and classifying them in terms of their topological characteristics. The result is a dynamical picture of the system, called the “phase portrait.” The mathematical methods for analyzing phase portraits are based on the pioneering work done by Henri Poincaré at the beginning of the twentieth century, and were further developed and refined by the American topologist Stephen Smale in the early 1960s.
BIFURCATIONS
Smale also discovered that in many nonlinear systems, small changes of certain parameters may produce dramatic changes in the basic characteristics of the phase portrait. Attractors may disappear, or change into one another, or new attractors may suddenly appear. Such systems are said to be structurally unstable, and their critical points of instability are called “bifurcation points.”
As there are only a small number of different types of attractors, so too there are only a small number of different types of bifurcation events, and like the attractors the bifurcations can be classified topologically. One of the first to do so was the French mathematician René Thom in the 1970s, who used the term “catastrophes” instead of bifurcations and identified seven elementary catastrophes. Today mathematicians know about two dozen bifurcation types.
Mathematically, bifurcation points mark sudden changes in the system's phase portrait. Physically, they correspond to points of instability at which the system changes abruptly and new forms of order suddenly appear. The discovery of this spontaneous emergence of order at critical points of instability is one of the most important discoveries of complexity theory.
ACHIEVEMENTS AND STATUS OF COMPLEXITY THEORY
Let me now turn to the achievements and current status of complexity theory. We need to remember first of all that complexity theory, or nonlinear dynamics, is not a scientific theory, in the sense of an empirically based analysis of natural or social phenomena. It is a mathematical theory, that is, a body of mathematical concepts and techniques for the description of nonlinear systems. As we have seen, to describe nonlinear systems mathematically, and to solve the corresponding equations, is radically different from the conventional linear descriptions. The most important achievement of nonlinear dynamics, in my view, is to provide the appropriate language for dealing with nonlinear systems.
I have discussed some of the key concepts of this language: chaos, attractors, fractals, bifurcation diagrams, qualitative analysis, and so on. Twenty-five years ago these concepts did not exist. Now we know what kinds of questions to ask when dealing with nonlinear systems.
Having the appropriate mathematical language does not mean that you know how to construct a mathematical model in a particular case. You need to simplify a highly complex system by choosing a few relevant variables, and then you need to set up the proper equations to interconnect these variables; or you can try to build a computer simulation. This is the interface between science and mathematics.
So the creation of a new language is the overall achievement of nonlinear dynamics. Then there are partial achievements in various fields, and among those I shall concentrate on the life sciences, the understanding of living systems.
THEORY OF DISSIPATIVE STRUCTURES
The Russian-born chemist and Nobel Laureate Ilya Prigogine was one of the first to use nonlinear dynamics to explore basic properties of living systems. What intrigued Prigogine most was that living organisms are able to maintain their life processes under conditions of nonequilibrium. During the 1960s, he became fascinated by systems far from equilibrium and began a detailed investigation to find out under exactly what conditions nonequilibrium situations may be stable.
The crucial breakthrough occurred when he realized that systems far from equilibrium must be described by nonlinear equations. The clear recognition of this link between “far from equilibrium” and “nonlinearity” opened an avenue of research for Prigogine that would culminate a decade later in his theory of dissipative structures, formulated in the language of nonlinear dynamics (see Capra, 1996: 172ff).
As mentioned before, a living organism is an open system that maintains itself in a state far from equilibrium and yet is stable: The same overall structure is maintained in spite of an ongoing flow and change of components. Prigogine called the open systems described by his theory “dissipative structures” to emphasize this close interplay between structure on the one hand and flow and change (or dissipation) on the other. The farther a dissipative structure is from equilibrium, the greater its complexity and the higher the degree of nonlinearity in the mathematical equations describing it.
The dynamics of these dissipative structures specifically include the spontaneous emergence of new forms of order. When the flow of energy increases, the system may encounter a point of instability, or bifurcation point, at which it can branch off into an entirely new state where new structures and new forms of order may emerge.
This spontaneous emergence of order at critical points of instability, often simply referred to as “emergence,” is one of the most important concepts of the new understanding of life. Emergence is one of the hallmarks of life. It has been recognized as the dynamic origin of development, learning, and evolution. In other words, creativity—the generation of new forms—is a key property of all living systems. And since emergence is an integral part of the dynamics of open systems, this means that open systems develop and evolve. Life constantly reaches out into novelty.
The theory of dissipative structures not only explains the spontaneous emergence of order, but also helps us define complexity. Whereas traditionally the study of complexity has been a study of complex structures, the focus is now shifting from the structures to the processes of their emergence. For example, instead of defining the complexity of an organism in terms of the number of its different cell types, as biologists often do, we can define it as the number of bifurcations through which the embryo goes in the organism's development. Accordingly, the British biologist Brian Goodwin (1998) speaks of “morphological complexity.”
CELL DEVELOPMENT
The theory of emergence, known to mathematicians as “bifurcation theory,” has been studied extensively by mathematicians and scientists, among them the American biologist Stuart Kauffman. Kauffman (1991; see also Capra, 1996: 194ff) used nonlinear dynamics to construct binary models of genetic networks and was remarkably successful in predicting some key features of cell differentiation.
A binary network, also called a “Boolean network,” consists of nodes capable of two distinct values, conventionally labeled ON and OFF. The nodes are coupled to one another in such a way that the value of each node is determined by the prior values of neighboring nodes according to some “switching rule.”
When Kauffman studied genetic networks, he noticed that each gene in the genome is directly regulated by only a few other genes, and he also knew that genes are turned on and off in response to specific signals. In other words, genes do not simply act; they must be activated. Molecular biologists speak of patterns of “gene expression.”
This gave Kauffman the idea of modeling genetic networks and patterns of gene expression in terms of binary networks with certain switching rules. The succession of ON-OFF states in these models is associated with a trajectory in phase space and is classified in terms of different types of attractors.
Extensive examination of a wide variety of complex binary networks has shown that they exhibit three broad regimes of behavior: an ordered regime with frozen components (i.e., nodes that remain either ON or OFF), a chaotic regime with no frozen components (i.e., nodes switching back and forth between ON and OFF), and a boundary region between order and chaos where frozen components just begin to change.
Kauffman's central hypothesis is that living systems exist in that boundary region near the so-called edge of chaos. He believes that natural selection may favor and sustain living systems at the edge of chaos, because these may be best able to coordinate complex and flexible behavior. To test his hypothesis, Kauffman applied his model to the genetic networks in living organisms and was able to derive from it several surprising and rather accurate predictions.
In terms of complexity theory, the development of an organism is characterized by a series of bifurcations, each corresponding to a new cell type. Each cell type corresponds to a different pattern of gene expression, and hence to a different attractor. The human genome contains between 30,000 and 100,000 genes. In a binary network of that size, the possibilities of different patterns of gene expression are astronomical. However, Kauffman could show that at the edge of chaos the number of attractors in such a network is approximately equal to the square root of the number of its elements. Therefore, the human network of genes should express itself in approximately 245 different cell types. This number comes remarkably close to the 254 distinct cell types identified in humans.
Kauffman also tested his attractor model with predictions of the number of cell types for various other species, and again the agreement with the actual numbers observed was very good.
Another prediction of Kauffman's attractor model concerns the stability of cell types. Since the frozen core of the binary network is identical for all attractors, all cell types in an organism should express mostly the same set of genes and should differ by the expressions of only a small percentage of genes. This is indeed the case for all living organisms.
In view of the fact that these binary models of genetic networks are quite crude, and that Kauffman's predictions are derived from the models' very general features, the agreement with the observed data must be seen as a remarkable success of nonlinear dynamics.
THE ORIGIN OF BIOLOGICAL FORM
A very rich and promising area for complexity theory in biology is the study of the origin of biological form, known as morphology. This is a field of study that was very lively in the eighteenth century, but then was eclipsed by the mechanistic approach to biology, until it made a comeback very recently with the emphasis of nonlinear dynamics on patterns and shapes.
A key insight of the new understanding of life has been that biological forms are not determined by a “genetic blueprint,” but are emergent properties of the entire epigenetic network of metabolic processes.
To understand the emergence of biological form, we need to understand not only the genetic structures and the cell's biochemistry, but also the complex dynamics that unfold when the epigenetic network encounters the physical and chemical constraints of its environment. In this encounter, the interactions between the organism's physical and chemical variables are highly complex and can be represented in simplified models by nonlinear equations. The solutions of these equations, represented by a limited number of attractors, correspond to the limited number of possible biological forms.
This technique has been applied to a variety of biological forms, from branching patterns of plants and the coloring of sea shells to the nest building of termites. An good example is the work of Brian Goodwin (1994: 77ff), who used nonlinear dynamics to model the stages of development of a single-celled Mediterranean alga, called Acetabularia, which forms beautiful little “parasol” caps (see Figure 3).

Figure 3 Acetabularia Acetabulum, attached to a rock in its natural habitat, the Mediterranean
Like the cells of plants and animals, the cell of this alga is shaped and sustained by its cytoskeleton, a complex and intricate structure of protein filaments. The cytoskeleton is subject to various mechanical stresses, and it turns out that a key influence on its mechanical state—its rigidity or softness—is the calcium concentration in the cell. The cytoskeleton is anchored to the cell wall, and its behavior under the mechanical stresses, therefore, gives rise to the alga's biological form.
Since the mechanical properties of the cytoskeleton at the molecular level are far too complex to be described mathematically, Goodwin and his colleagues approximated them by a continuous field, known in physics as a stress-tensor field. They were then able to set up nonlinear equations that interrelate patterns of calcium concentration in the alga's cell fluid with the mechanical properties of the cell walls.
These equations contained numerous parameters, such as the diffusion constant for calcium, the resistance of the cytoskeleton to deformation, and so on. In nature, these quantities are determined genetically and change from species to species, so that different species produce different biological forms.
Goodwin and his colleagues proceeded to try out a variety of parameters in computer simulations to explore the types of form that a developing alga could produce. They succeeded in simulating a whole sequence of structures that appear in the alga's development of its characteristic stalk and parasol (see Figure 4). These forms emerged as successive bifurcations of the attractors representing the interplay between patterns of calcium and mechanical strain.
The lesson to be learned from these models of plant morphology is that biological form emerges from the nonlinear dynamics of the organism's epigenetic network as it interacts with the physical constraints of its molecular structures. The genes do not provide a blueprint for biological forms. They provide the initial conditions that determine which kind of dynamics—or, mathematically, which kind of attractors—will appear in a given species. In this way genes stabilize the emergence of biological form.
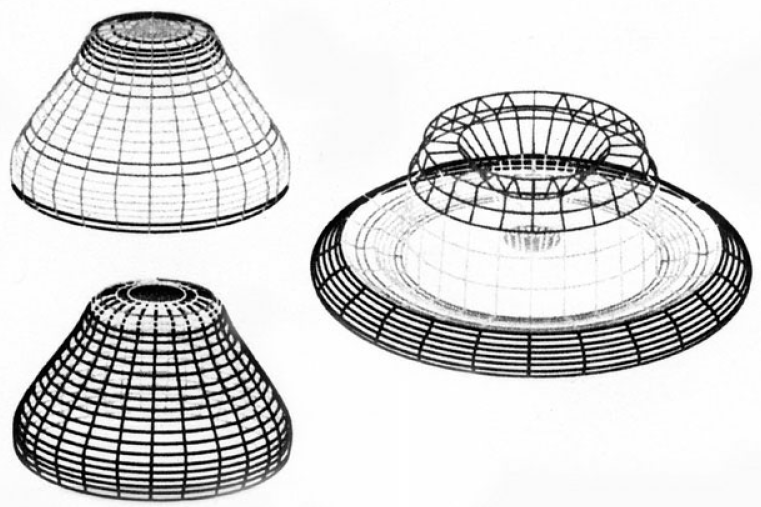
Figure 4 Computer simulations of algal structures, arising from the interplay between patterns of calcium concentration and mechanical strain
DEVELOPMENTAL STABILITY
From the origin of biological form, let me move on to the development of an embryo (Capra, 2002: 152-3). Complexity theory may shed new light on an intriguing property of biological development that was discovered almost 100 years ago by the German embryologist Hans Driesch. With a series of careful experiments on sea urchin eggs, Driesch showed that he could destroy several cells in the very early stages of the embryo, and it would still grow into a full, mature sea urchin. Similarly, more recent genetic experiments have shown that “knocking out” single genes, even when they were thought to be essential, had very little effect on the functioning of the organism.
This very remarkable stability and robustness of biological development mean that an embryo may start from different initial stages—for example, if single genes or entire cells are destroyed accidentally—but will nevertheless reach the same mature form that is characteristic of its species. The question is, what keeps development on track?
There is an emerging consensus among genetic researchers that this robustness indicates a redundancy in genetic and metabolic pathways. It seems that cells maintain multiple pathways for the production of essential cellular structures and the support of essential metabolic processes. This redundancy ensures not only the remarkable stability of biological development but also great flexibility and adaptability to unexpected environmental changes. Genetic and metabolic redundancy may be seen, perhaps, as the equivalent of biodiversity in ecosystems. It seems that life has evolved ample diversity and redundancy at all levels of complexity.
The observation of genetic redundancy is in stark contradiction to genetic determinism, and in particular to the metaphor of the “selfish gene” proposed by British biologist Richard Dawkins. According to him, genes behave as if they were selfish by constantly competing, via the organisms they produce, to leave more copies of themselves. From this reductionist perspective, the widespread existence of redundant genes makes no evolutionary sense. From a systemic point of view, by contrast, we recognize that natural selection operates not on individual genes but on the organism's patterns of self-organization. In other words, what is selected by nature is not the individual gene but the endurance of the organism's life cycle.
The existence of multiple pathways is an essential property of all networks; it may even be seen as the defining characteristic of a network. It is therefore not surprising that complexity theory, which is eminently suited to the analysis of networks, should contribute important insights into the nature of developmental stability.
In the language of nonlinear dynamics, the process of biological development is seen as a continuous unfolding of a nonlinear system as the embryo forms out of an extended domain of cells. This “cell sheet” has certain dynamical properties that give rise to a sequence of deformations and foldings as the embryo emerges. The entire process can be represented mathematically by a trajectory in phase space moving inside a basin of attraction toward an attractor that describes the functioning of the organism in its stable adult form.
A characteristic property of complex nonlinear systems is that they display a certain “structural stability.” A basin of attraction can be disturbed or deformed without changing the system's basic characteristics. In the case of a developing embryo this means that the initial conditions of the process can be changed to some extent without seriously disturbing development as a whole. Thus developmental stability, which seems quite mysterious from the perspective of genetic determinism, is recognized as a consequence of a very basic property of complex nonlinear systems.
ORIGIN OF LIFE
My last example of applying complexity theory to problems in biology is not about an actual achievement but about the potential for a major breakthrough in solving an old scientific puzzle—the question of the origin of life on Earth (Capra, 2002: 17ff).
Ever since Darwin, scientists have debated the likelihood of life's emerging from a primordial “chemical soup” that formed four billion years ago when the planet cooled off and the primeval oceans expanded. The idea that small molecules should assemble spontaneously into structures of ever-increasing complexity runs counter to all conventional experience with simple chemical systems. Many scientists have therefore argued that the odds of such prebiotic evolution are vanishingly small; or, alternatively, that there must have been an extraordinary triggering event, such as a seeding of the Earth with macromolecules by meteorites.
Today, our starting position for resolving this puzzle is radically different. Scientists working in this field have come to recognize that the flaw of the conventional argument lies in the idea that life must have emerged out of a chemical soup through the progressive increase of molecular complexity. The new thinking begins from the hypothesis that very early on, before the increase of molecular complexity, certain molecules assembled into primitive membranes that spontaneously formed closed bubbles, and that the evolution of molecular complexity took place inside these bubbles, rather than in a structureless chemical soup.
It turns out that small bubbles, known to chemists as vesicles, form spontaneously when there is a mixture of oil and water, as we can easily observe when we put oil and water together and shake the mixture. Indeed, the Italian chemist Pier Luigi Luisi (1996) and his colleagues at the Swiss Federal Institute of Technology have repeatedly prepared appropriate “water-and-soap” environments in which vesicles with primitive membranes, made of fatty substances known as lipids, formed spontaneously.
Biologist Harold Morowitz (1992) has developed a detailed scenario for prebiotic evolution along these lines. He points out that the formation of membrane-bounded vesicles in the primeval oceans created two different environments—an outside and an inside—in which compositional differences could develop. The internal volume of a vesicle provides a closed micro-environment in which directed chemical reactions can occur, which means that molecules that are normally rare may be formed in great quantities. These molecules include in particular the building blocks of the membrane itself, which become incorporated into the existing membrane, so that the whole membrane area increases. At some point in this growth process the stabilizing forces are no longer able to maintain the membrane's integrity, and the vesicle breaks up into two or more smaller bubbles.
These processes of growth and replication will occur only if there is a flow of energy and matter through the membrane. Morowitz describes a plausible scenario of how this might have happened. The vesicle membranes are semipermeable, and thus various small molecules can enter the bubbles or be incorporated into the membrane. Among those will be so-called chromophores, molecules that absorb sunlight. Their presence creates electric potentials across the membrane, and thus the vesicle becomes a device that converts light energy into electric potential energy.
Once this system of energy conversion is in place, it becomes possible for a continuous flow of energy to drive the chemical processes inside the vesicle.
At this point we see that two defining characteristics of cellular life are manifest in rudimentary form in these primitive membrane-bounded bubbles. The vesicles are open systems, subject to continual flows of energy and matter, while their interiors are relatively closed spaces in which networks of chemical reactions are likely to develop. We can recognize these two properties as the roots of living networks and their dissipative structures.
Now the stage is set for prebiotic evolution. In a large population of vesicles there will be many differences in their chemical properties and structural components. If these differences persist when the bubbles divide, we can speak of “species” of vesicles, and since these species will compete for energy and various molecules from their environment, a kind of Darwinian dynamics of competition and natural selection will take place, in which molecular accidents may be amplified and selected for their “evolutionary” advantages.
Thus we see that a variety of purely physical and chemical mechanisms provide the membrane-bounded vesicles with the potential to “evolve” through natural selection into complex, self-producing structures without enzymes or genes in these early stages.
A dramatic increase in molecular complexity must have occurred when catalysts, based on nitrogen, entered the system, because catalysts create complex chemical networks by interlinking different reactions. Once this happens, the entire nonlinear dynamics of networks, including the spontaneous emergence of new forms of order, comes into play.
The final step in the emergence of life was the evolution of proteins, nucleic acids, and the genetic code. At present, the details of this stage are still quite mysterious. However, we need to remember that the evolution of catalytic networks within the closed spaces of the protocells created a new type of network chemistry that is still very poorly understood. This is where complexity theory could lead to decisive new insights. We can expect that the application of nonlinear dynamics to these complex chemical networks will shed considerable light on the last phase of prebiotic evolution.
Indeed, Morowitz points out that the analysis of the chemical pathways from small molecules to amino acids reveals an extraordinary set of correlations that seem to suggest, as he puts it, a “deep network logic” in the development of the genetic code. The future understanding of this network logic may become one of the greatest achievements of complexity theory in biology.
CONCLUSION
I have reviewed some of the most important achievements of complexity theory in the life sciences. At present, the mathematical language of nonlinear dynamics is still very new, and many scientists are not familiar with it. However, this is bound to change as we become more and more aware of the importance of nonlinear phenomena at all levels of life. Whenever scientists engage seriously in modeling nonlinear systems, especially in biology, complexity theory will be an essential tool. Indeed, according to neuroscientist and Nobel Laureate Gerald Edelman (1998), “The understanding of complexity is the central problem of biology today.” And British mathematician Ian Stewart (1998: xii) writes:
I predict—and I am by no means alone—that one of the most exciting growth areas of twenty-first-century science will be biomathematics. The next century will witness an explosion of new mathematical concepts, of new kinds of mathematics, brought into being by the need to understand the patterns of the living world.
References
Capra, Fritjof (1996) The Web of Life, London: HarperCollins.
Capra, Fritjof (2002) The Hidden Connections, London: HarperCollins.
Edelman, Gerald (1998) personal communication.
Fox Keller, Evelyn (2000) The Century of the Gene, Cambridge, MA: Harvard University Press.
Goodwin, Brian (1994) How the Leopard Changed Its Spots, New York: Scribner.
Goodwin, Brian (1998) personal communication.
Kauffman, Stuart (1991) “Anti-chaos and adaptation,” Scientific American, August.
Luisi, Pier Luigi (1996) “Self-reproduction of micelles and vesicles,” in I. Prigogine & S. A. Rice (eds), Advances in Chemical Physics, Vol. XCII, Chichester, UK: Wiley.
Morowitz, Harold (1992) Beginnings of Cellular Life, New Haven, CT: Yale University Press.
Stewart, Ian (1998) Life's Other Secret, Chichester, UK: Wiley.