Ecology, a Dialog between the Quick and the Dead
Robert E. Ulanowicz
University of Maryland, USA
Introduction
At a recent lecture hosted by the American Academy for the Advancement of Science, John Haught (2001a) outlined the two extremes between which philosophical opinions on the core issues of life and death have shifted over the last three centuries. He related that before the seventeenth century life was regarded as ubiquitous and ascendant. It was perceived to be everywhere, even in what now is commonly regarded as purely physical phenomena. The chief problem for pre-Enlightenment philosophers, therefore, was to explain the exceptional nature of death.
With the dawn of the Enlightenment, the pendulum swung radically in the opposite direction. The preponderance of the universe is now considered to consist of dead, quiescent matter that moves according to deterministic and inexorable laws, which by their simple natures appear to leave no room for the irreversible, asymmetric, and contingent phenomena associated with living systems. Under the Enlightenment vision, ontological priority is accorded to dead material, resulting in what Paul Tillich has called “the ontology of death.” Haught (2001b) adds that such an ontology leads to a “cosmology of despair.” Under such presuppositions, it should come as no surprise that the one of the most pressing scientific and philosophical questions of our day has become the emergence of life: How could it possibly have arisen from such a dead universe?
When this shift in assumptions is regarded from a millennial perspective, the possibility that humanity has been entertaining in its turn two unrealistic extremes cannot easily be dismissed. Might there exist an excluded metaphysical middle ground, one that is centered more toward the interface between the quick and the dead? We note, for example, that over the course of the twentieth century physicists have been backtracking ever so slowly from the overzealous application of Occam's Razor that had culminated in the Newtonian metaphysics of the early nineteenth century (Capra, 1975). Biologists, however, have been reluctant to follow suit (e.g., Dennett, 1995). I wish to suggest that if we are to search for such a middle ground, there is no more appropriate concept with which to begin than with the ecosystem, which Tansley (1935) defined as the combination of the living community of organisms, acting with the nonliving (dead) elements of their environment as a functional unit.
Our choice of ecology as the discipline in which to begin the search for a revised perspective is reinforced, furthermore, by the feeling widespread among investigators in many fields that there is something special about ecology. Why else would so many diverse researchers wish to cloak their own endeavors with the mantle of ecology? One encounters, for example, books on “the ecology of computational systems” (Huberman, 1988) or entire institutes devoted to “the ecological study of perception and action” (Gibson, 1979). I wish to suggest that this predilection on the part of many to assume the guise of ecology for their work derives at least in part from a recognition that ecology spans the interface between the quick and the dead. In fact, the subdiscipline of ecosystems research is often pursued under fundamental assumptions that depart markedly from those that have channeled our worldview over the past two centuries.
Before we try to formalize those ecological presuppositions, we need first to review the basic postulates that guided science during its “classical” early period in the nineteenth century, so that we may establish a set of references against which to distinguish the ecological vision.
According to Depwe and Weber (1994), science during the nineteenth century was overwhelmingly Newtonian in scope. They identified four postulates under which Newtonian investigations were pursued:
- Newtonian systems are causally closed. Only mechanical or material causes are legitimate. Newtonian systems are dead.
- Newtonian systems are deterministic. Given precise initial conditions, the future (and past) states of a system can be specified with arbitrary precision. Newtonian systems are driven wholly from the outside.
- Newtonian systems are reversible. Laws governing behavior work the same way in both temporal directions.
- Newtonian systems are atomistic. They are strongly decomposable into stable least units, which can be built up and taken apart again.
After consulting with these authors, I have added a fifth article of faith (Ulanowicz, 1997), namely:
- Physical laws are universal. They apply everywhere, at all times and over all scales.
As mentioned above, ecologists are hardly the first to distance themselves from some of these five postulates. The notion of reversibility had been challenged early in the nineteenth century by Sadi Carnot's thermodynamical elaboration of irreversibility and several decades later by Darwin's historical narrative. The development of relativity and quantum theories early in the twentieth century served to bring into question the assumptions of universality and determinism respectively. As a result, almost no one still adheres to all five postulates. Most biologists (and even many ecologists) still cling, however, to the general Newtonian framework. Fortunately, not all do so.
In his historical analysis of ecosystems theory, Joel Hagen (1992) identified three distinct metaphors by means of which ecologists have attempted to make sense of ecological phenomena. The most familiar and widely accepted metaphor is that of the ecosystem as a (dead) machine, or clockwork, which, of course, runs according to the Newtonian scenario. This tradition has been kept alive and well by the likes of George Clarke (1954), Howard Odum (1960), and Thomas Schoener (1986). Interestingly, however, the mechanical metaphor was preceded in the ecological arena by Frederic Clements' (1916) suggestion that ecosystems behave like (living) organisms. Clements directly credited Jan Smuts (1926) as his inspiration, but ultimately he was following in the traditions of Leibniz and Aristotle. The organic analogy was advanced in subsequent decades by G. Evelyn Hutchinson and Eugene Odum.
Finally, a contemporary of Clements, Henry Gleason (1917), countered the notion of ecosystems as organisms with the idea that ecological communities arise largely by chance and in the absence of any major organizational influences. Such stochasticism follows the lead of nominalism and deconstructivist postmodernism (Haught's “cosmology of despair”) and has found voice in contemporary ecology through the writings of Daniel Simberloff (1980), Kristin Schrader-Frechette (Schrader-Frechette & McCoy, 1993), and Mark Sagoff (1997), all of whom deride the mechanical and organic metaphors as unwarranted realism.
ECOSYSTEMS AND CONTINGENCY
One of the key attributes of living systems is their tendency to exhibit chance, unpredictable behaviors. Reconciling chance with deterministic mechanics is no easy task, and the problem has challenged some of the best minds over the past two centuries. Because the various attempts at reconciliation were so limited in scope, biology remains somewhat “schizophrenic” in nature, much like the polar attitudes as to whether the universe is fundamentally living or dead cited above. Narrative constantly is switching back and forth between the realms of strict determinism and pure stochasticity, as if no middle ground existed.
In referring to this regrettable situation, Karl Popper (1990) remarked that it still remains for us to achieve a truly “evolutionary theory of knowledge,” and we will not do so until we reconsider our fundamental attitudes toward the nature of causality. True reconciliation, Popper suggested, lies intermediate to stochasticity and determinism. He proposed, therefore, a generalization of the Newtonian notion of “force.” Forces, he posited, are idealizations that exist as such only in perfect isolation, like the cold, nonliving environment of outer space. The objective of experimentation is to approximate such isolation from interfering factors as well as possible. In the real world, however, where components are loosely but definitely coupled, one should speak rather of “propensities.” A propensity is the tendency for a certain event to occur in a particular context. It is related to, but not identical to, conditional probabilities.
Deterministic systems are characterized by certainty: If A, then B—no exceptions! On the other hand, stochastic events are completely independent of past or surrounding events. With propensities, however, the frequency with which an event might occur can be influenced strongly by antecedent events (history) and contemporary surroundings (including other propensities).
This interconnectedness of propensities highlights an unsung aspect of the role of contingency in systems development; namely, that contingencies are not always simple in nature. Chance events can possess highly distinct characteristics, making them rare or possibly even unique in occurrence. The conventional wisdom, however, is to consider chance events as being almost point-like in extent and instantaneous in duration. In fact, we rarely ever think of chance events as anything but simple and generic. Thus, when Prigogine (Prigogine & Stengers, 1984) writes about macroscopic order appearing via microscopic fluctuations, it is implicit that the latter are generic and structureless. Perturbations, however, happen to come in an infinite variety of forms, and any given system may be very vulnerable to some categories of disturbance and rather immune to others. In short, contingencies can be complex (Ulanowicz, 2001).
Even if disturbances should come in different flavors, a further implicit assumption commonly made is that any individual type of disturbance will always occur repeatedly. The repetition of phenomena is, after all, the Baconian cornerstone of normal science. Once one allows that contingencies may be complex, however, one must face up to the possibility that some contingencies might be unique once and for all time. In fact, it is even necessary to confront the likelihood that our world might be absolutely rife with one-time events. That such might be the case follows as soon as one ceases to regard contingencies merely as simple point events, but rather as configurations or constellations of both things and processes.
Because propensities always exist in a context (in accordance with the ecological vision), and because that context usually is not simple, it becomes necessary to consider the reality and nature of complex contingencies. To capture the effects of chance, it won't suffice simply to modulate the parameters of a mechanical model with generic noise (cf. Patten, 1999). In a complex world unique events occur continually. Perhaps fortunately, the overwhelming majority of one-time events happen and pass from the scene without leaving a trace in the more enduring observable universe. On occasion, however, a singular contingency can interact with a durable system in such a way that the system readjusts in an irreversible way to the disturbance. The system then carries the memory of that contingency as part of its history. No amount of waiting is likely to lead to an uncontrived repetition of what has transpired.
The efficacy of Popper's concept of propensity is that it pertains equally well to law-like behavior, generic chance, and unique contingencies, all under a single rubric. We note for reference below that the concept of development generally involves proceeding from less constrained to more constrained circumstances. We now ask the questions: “What lies behind the phenomena we call growth and development?” and “How can one quantify the effects of this agency?”
AUTOCATALYSIS AND ORGANIC SYSTEMS
One clue to an agency behind growth and development appears as soon as one considers what happens when propensities act in close proximity to one another. Any one process will either abet (+), diminish (-), or not affect (0) another. Similarly, the second process can have any of the same effects on the first. Out of the nine possible combinations for reciprocal interaction, it turns out that one interaction, namely mutualism (+,+), has very different properties from all the rest. Investigators such as Manfred Eigen (1971), Hermann Haken (1988), Umberto Maturana (Maturana & Varela, 1980), Stuart Kauffman (1995), and Donald DeAngelis (DeAngelis et al., 1986) all have contributed to a growing consensus that some form of positive feedback is responsible for most of the order we perceive in organic systems.
I now wish to focus attention on a particular form of positive feedback, autocatalysis. Herein the effect of each and every link in the feedback loop remains positive. In words more germane to the theme of this article, one could say that the action of each and every element in the cycle quickens the activity of the next member (quicken meaning to make alive as well as to make more rapid). In the framework of Newtonian assumptions, as autocatalysis is usually viewed in chemistry, such feedback appears merely as a particular type of (dead) mechanism. As soon as one admits some form of indeterminacy, however, several highly nonmechanical attributes more characteristic of living systems suddenly emerge.
To be precise about the form of autocatalysis to which I am referring, I direct the reader's attention to the three-component interaction depicted in Figure 1. We assume that the action of process A has a propensity to augment a second process, B. I wish to emphasize my use of the word “propensity” to mean that the response of B to A is not wholly obligatory. That is, A and B are not tightly and mechanically linked.
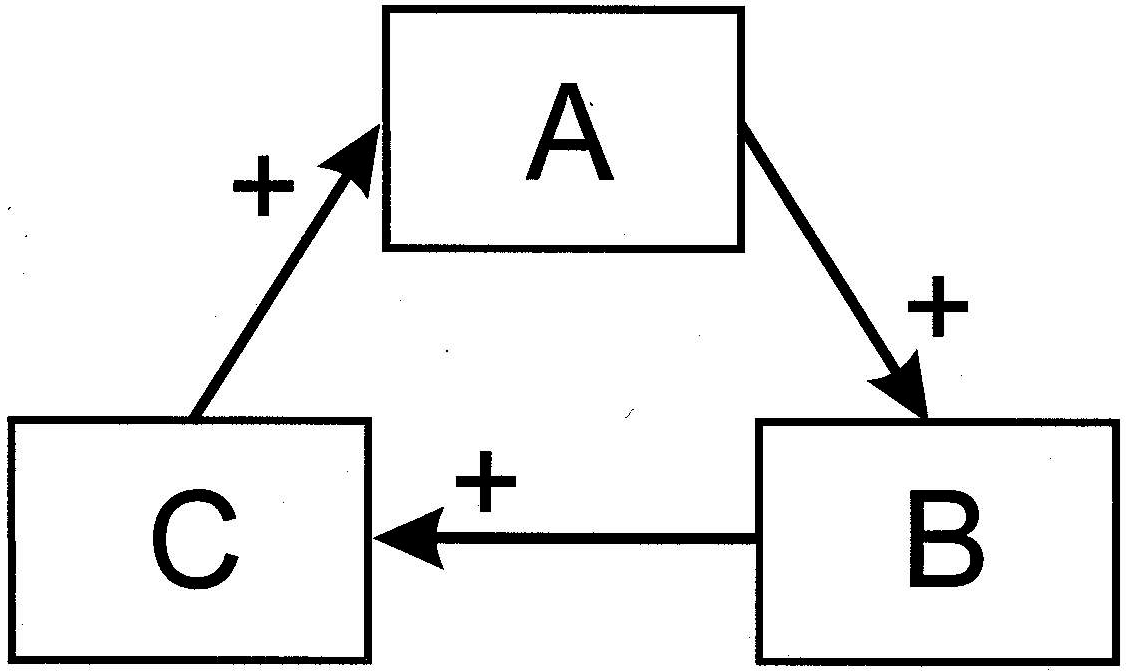
Figure 1 Schematic of a hypothetical three-component autocatalytic cycle
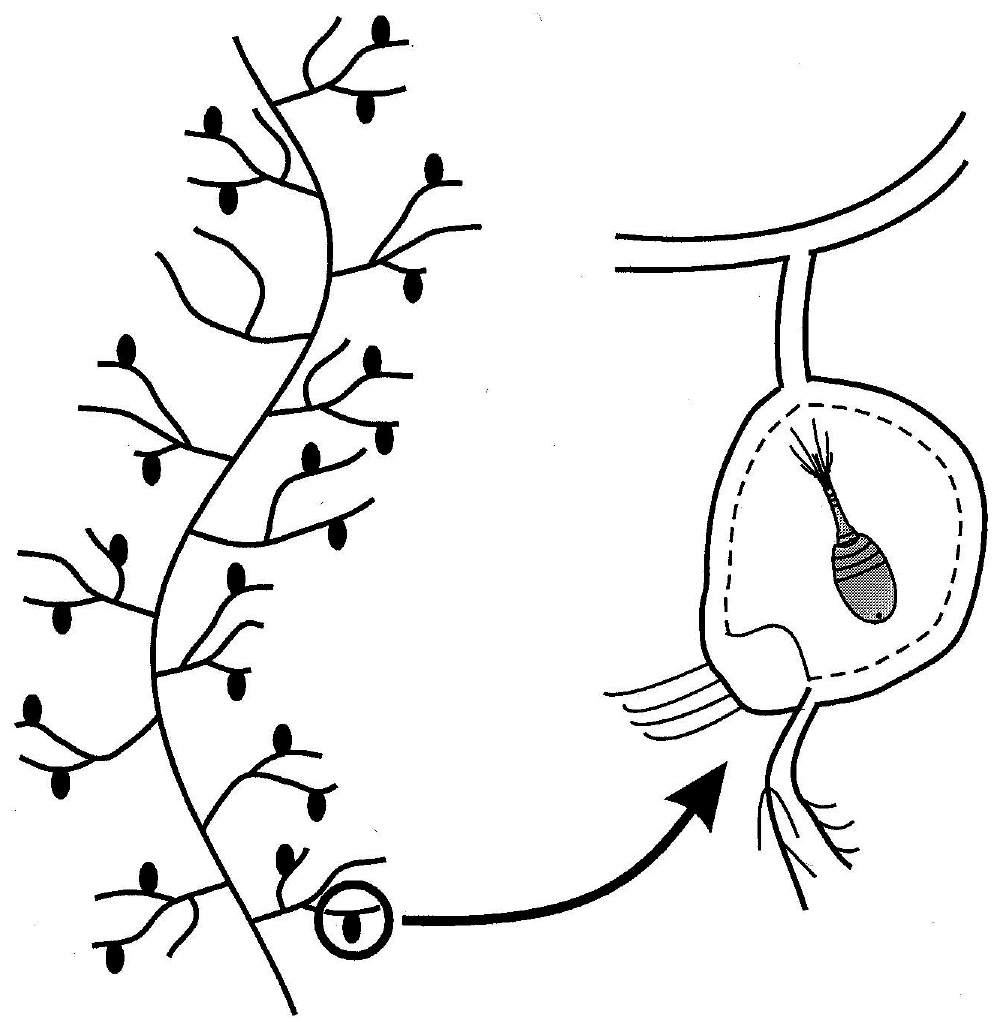
Figure 2a Sketch of a typical “leaf” of Utricularia floridana, with detail of the interior of an utricle containing a captured invertebrate
Rather, when process A increases in magnitude, most (but not all) of the time B also will increase. B tends to accelerate C in similar fashion, and C has the same effect on A. Chance is an important element in this form of feedback.
My favorite ecological example of autocatalysis is the community that centers around the aquatic macrophyte, Utricularia (Ulanowicz, 1995). All members of the genus Utricularia are carnivorous plants. Scattered along its feather-like stems and leaves are small bladders, called utricles (Figure 2a). Each utricle has a few hair-like triggers at its terminal end, which, when touched by a feeding zooplankton, opens the end of the bladder and the animal is sucked into the utricle by a negative osmotic pressure that the plant had maintained inside the bladder. In the field Utricularia plants always support a film of algal growth known as periphyton (Figure 2b). This periphyton in turn serves as food for any number of species of small zooplankton. The catalytic cycle is completed when the Utricularia captures and absorbs many of the zooplankton.
Autocatalysis among propensities gives rise to at least eight system attributes, which, taken as a whole, comprise a distinctly nonmechanical dynamic. We begin by noting that by our definition autocatalysis is explicitly growth enhancing, or quickening. Furthermore, autocatalysis exists as a formal structure of kinetic elements. More interestingly, however, autocatalysis is capable of exerting selection pressure on its ever-changing constituents.
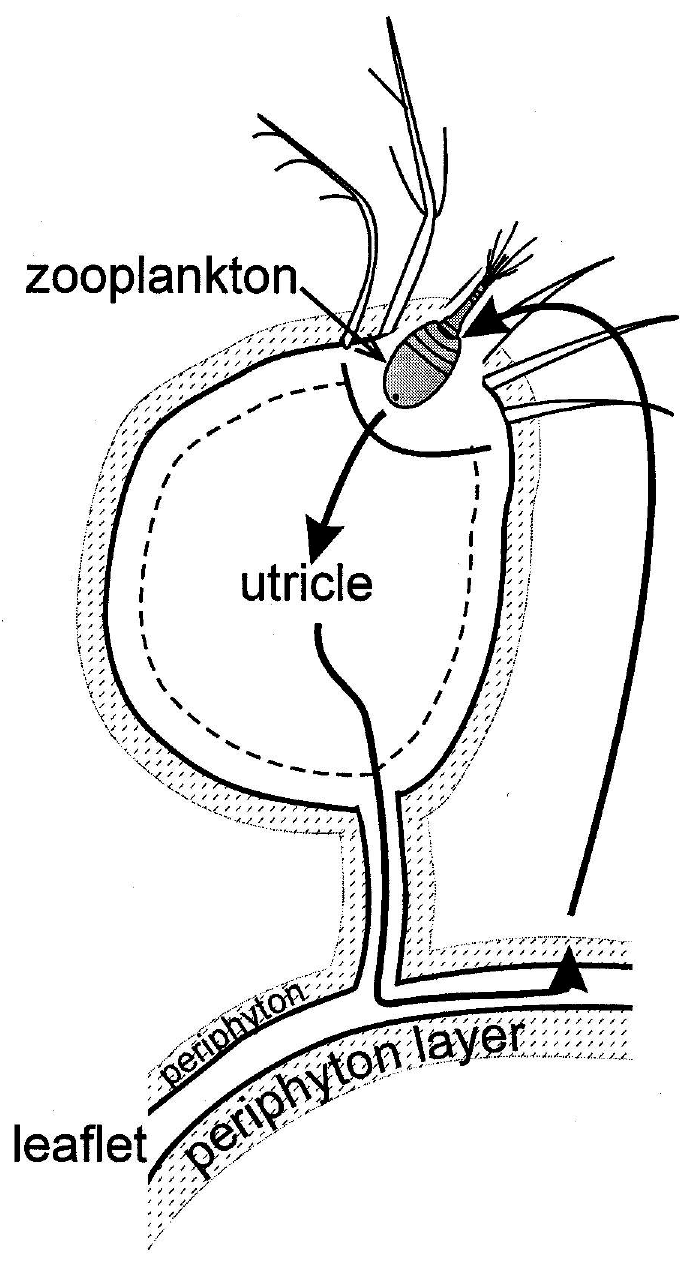
Figure 2b Schematic of the autocatalytic loop in the Utricularia system. Macrophyte provides the necessary surface on which periphyton (striped area) can grow. Zooplankton consumes periphyton and is itself trapped in the bladder and absorbed in turn by the Utricularia
To see this, let us suppose that some small change occurs spontaneously in process B. If that change makes B either more sensitive to A or a more effective catalyst of C, then the change will receive enhanced stimulus from A. Conversely, if the change in B makes it either less sensitive to the effects of A or a weaker catalyst of C, then that change will likely receive diminished support from A. We note that such selection works on the processes or mechanisms as well as on the elements themselves. Hence, any effort to describe or simulate development wholly in terms of a fixed set of mechanisms is doomed eventually to fail.
It should be noted in particular that any change in B is likely to involve a change in the amounts of material and energy that flow to sustain B; whence, as a corollary of selection pressure, we recognize the tendency to reward and support changes that bring ever more resources into B. As this circumstance pertains to all the other members of the feedback loop as well, any autocatalytic cycle becomes the center of a centripetal vortex, pulling as many of the needed resources as possible into its domain. In its centripetality the system is not acting passively at the behest of its environment. It is exhibiting active agency on those nonliving (and living) surroundings.
It follows that whenever two or more autocatalyic loops draw from the same pool of resources, autocatalysis will induce competition. In particular, we notice that whenever two loops partially overlap, the outcome could be the exclusion of one of the loops. In Figure 3, for example, element D is assumed to appear spontaneously in conjunction with A and C. If D is more sensitive to A and/or a better catalyst of C, then there is a likelihood that the ensuing dynamics will so favor D over B, that B will either fade into the background or disappear altogether. That is, selection pressure and centripetality can guide the replacement of elements. Of course, if B can be replaced by D, there remains no reason why C cannot be replaced by E or A by F, so that the cycle A, B, C could eventually transform into F, D, E. One concludes that the characteristic lifetime of the autocatalytic form usually persists beyond those of most of its constituents.
Autocatalytic selection pressure and the competition it engenders define a preferred direction for the system, that of ever more effective autocatalysis. In the terminology of physics, autocatalysis is symmetry breaking. One should not confuse this rudimentary directionality with full-blown teleology. It is not necessary, for example, that there exists a preordained end point toward which the system strives. The direction of the system at any one instant is defined by its state at that time, and the state changes as the system develops.
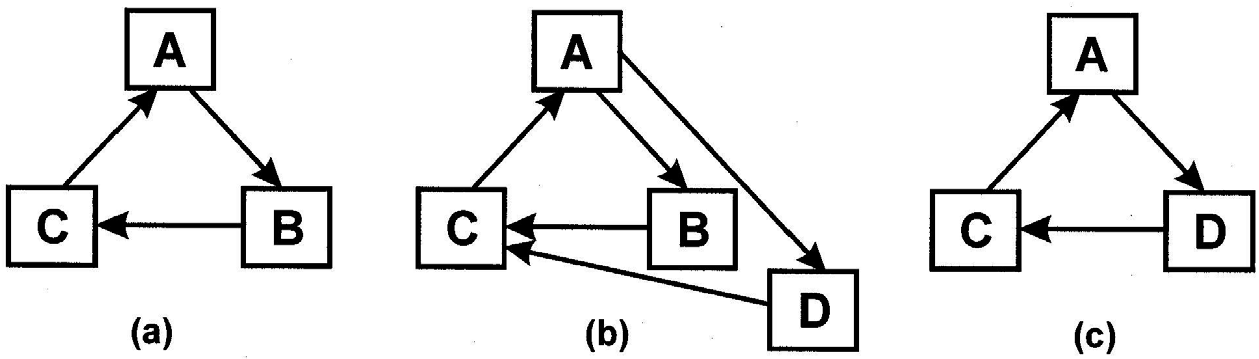
Figure 3 (a) Original configuration. (b) Competition between component B and a new component D, which is either more sensitive to catalysis by A or a better catalyst of C. (c) B is replaced by D and the loop section A-B-C by that of F-D-E
Taken together, selection pressure, centripetality, and a longer characteristic lifetime all speak to the existence of a degree of autonomy of the larger structure from its constituents. Again, attempts at reducing the workings of the system to the properties of its composite elements will remain futile over the long run. In particular, attempts to reduce living behaviors wholly to the agencies of nonliving components are likewise inappropriate.
In epistemological terms, the dynamics I have just described can be considered emergent. In Figure 4, if one should consider only those elements in the lower right-hand corner (as enclosed by the solid line), then one can identify an initial cause and a final effect. If, however, one expands the scope of observation to include a full autocatalytic cycle of processes (as enclosed by the dotted line), then the system properties I have just described appear to emerge spontaneously.
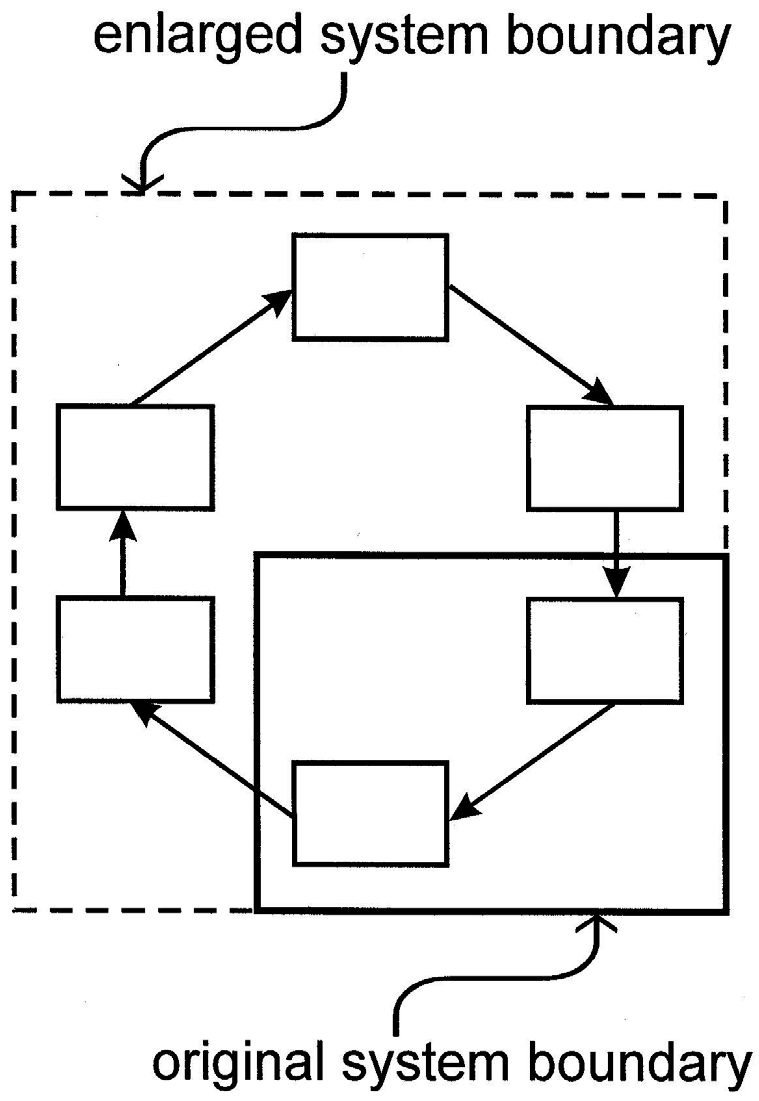
Figure 4 Two hierarchical views of an autocatalytic loop. The original perspective (solid line) includes only part of the loop, which therefore appears to function quite mechanically. A broader vision encompasses the entire loop, and with it several nonmechanical attributes
It is important to note that selection pressure arising from autocatalysis acts from higher scales downwards. Top-down influence is familiar to ecologists in the context of trophic interactions, but the Newtonian metaphysic allows only influences originating at lower realms of time and space to exert their effects at larger and longer scales. Prior to Newton, however, the prevailing view on natural causalities had been formulated by Aristotle, who explicitly recognized the existence of downward causation (Ulanowicz, 2001).
The Achilles heel of Newtonian-like dynamics is that it cannot in general accommodate true chance or indeterminacy (whence the “schizophrenia” in contemporary biology). Should a truly chance event happen at any level of a strictly mechanical hierarchy, all order at higher levels would be doomed eventually to unravel. By contrast, an Aristotelian hierarchy of causes is far more accommodating (and organic). Any spontaneous efficient agency at any hierarchical level is subject to selection pressures from formal autocatalytic configurations above. These configurations in turn experience selection from still larger constellations, and so on. One may conclude, thereby, that the influence of most irregularities remains circumscribed. Unless the larger structure is particularly vulnerable to a certain type of perturbation (and this happens relatively rarely), the effects of most perturbations are quickly dampened.
THE EXCLUDED ORGANIC MIDDLE GROUND
Popper has suggested that we should no longer be satisfied with the prevailing image of rigid mechanisms set opposite to complete disorder, if for no other reason than that the dichotomy leaves no room in between for the process of life. He therefore urges us to consider a middle ground, wherein propensities interacting with each other are behind the emergence of nonrigid structures that nonetheless retain their coherence over time. That is, he describes a world rife with the potential for life. The major problem with earlier organic metaphors has been that their proponents, such as Fredric Clements (1916), cast them in rigid, nonliving, mechanical terms. We turn our attention, therefore, to agencies that potentially could give rise to organic-like, nonrigid structures, and our focus returns once again to autocatalysis.
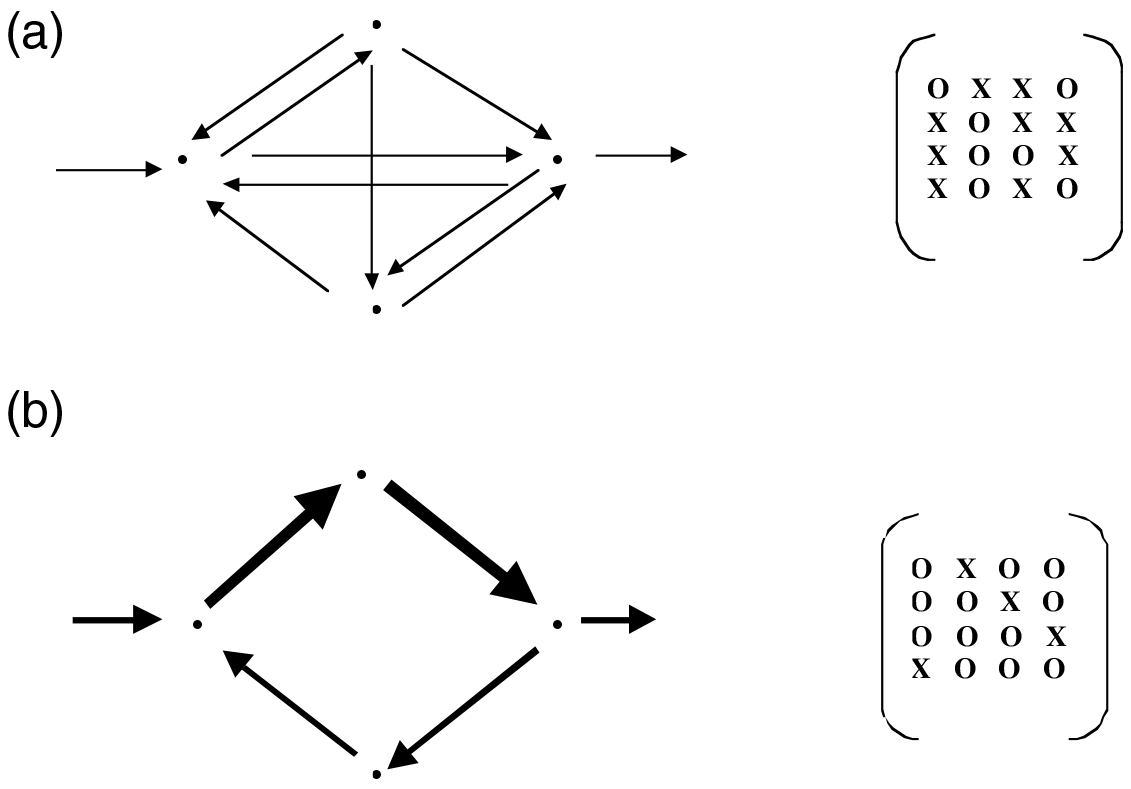
Figure 5 Schematic representation of the major effects that autocatalysis exerts on a system. (a) Original system configuration with numerous equiponderant interactions. (b) Same system after autocatalysis has pruned some interactions, strengthened others, and increased the overall level of system activity (indicated by the thickening of the arrows). Corresponding matrices of topological connections indicated to the right
Out of our considerations on autocatalysis we abstract two major facets of its actions: Autocatalysis serves to increase the activities of all its constituents, and it prunes the network of interactions so that those links that most effectively participate in autocatalysis become dominant. Schematically this transition is depicted in Figure 5. The upper figure represents a hypothetical, inchoate four-component network before autocatalysis has developed, and the lower one the same system after autocatalysis has matured. The magnitudes of the flows are represented by the thicknesses of the arrows.
There is not sufficient space to present in full detail how the two facets of autocatalysis can be quantified. We have room only to sketch out qualitatively the major points. We begin by choosing as the factor that best gauges the extent of system activity the simple sum of the magnitudes of all the system processes, or what has been called elsewhere the “total system throughput” (Finn, 1976). Growth thereby becomes an increase in the total system throughput, much as economic growth is reckoned by any increase in a very similar measure, gross domestic product.
As for the “pruning” or the intensive (scale-independent) development effected by autocatalysis, it is the manifestation of progressive constraints that appear in the system to guide flows along those links that most effectively contributes to autocatalysis itself. We can never know all these constraints nor full details about them. Such ignorance, however, does not preclude us from being able to measure their effects. (If this sounds strange to some readers, they should recall that in thermodynamics one measures the macroscopic properties of matter in complete abstraction from the molecular details that bring about those attributes.) The measure we use to gauge the “pruning” is taken from information theory and is called the “average mutual information” (Ulanowicz, 1980).
To give the reader an idea of what the average mutual information (AMI) represents, we consider a quantum of medium leaving a system compartment. If there are few constraints on where next that quantum might flow, the contribution to the average constraint will be small. Conversely, if many constraints exist that serve to “channel” or direct the quantum to only one or a very few other compartments, then the contribution to the average constraint will be proportionately large. The average mutual information (or more accurately the average constraint) will behave as shown by the three hypothetical configurations in Figure 6. In configuration (a) where medium from any one compartment will next flow is maximally indeterminate. Constraints are completely missing, so that the average constraint is identically zero. The possibilities in network (b) are somewhat more constrained. Flow exiting any compartment can proceed to only two other compartments, and the AMI rises accordingly. Finally, flow in schema (c) is maximally constrained, and the AMI assumes its maximal value for a network of dimension four.
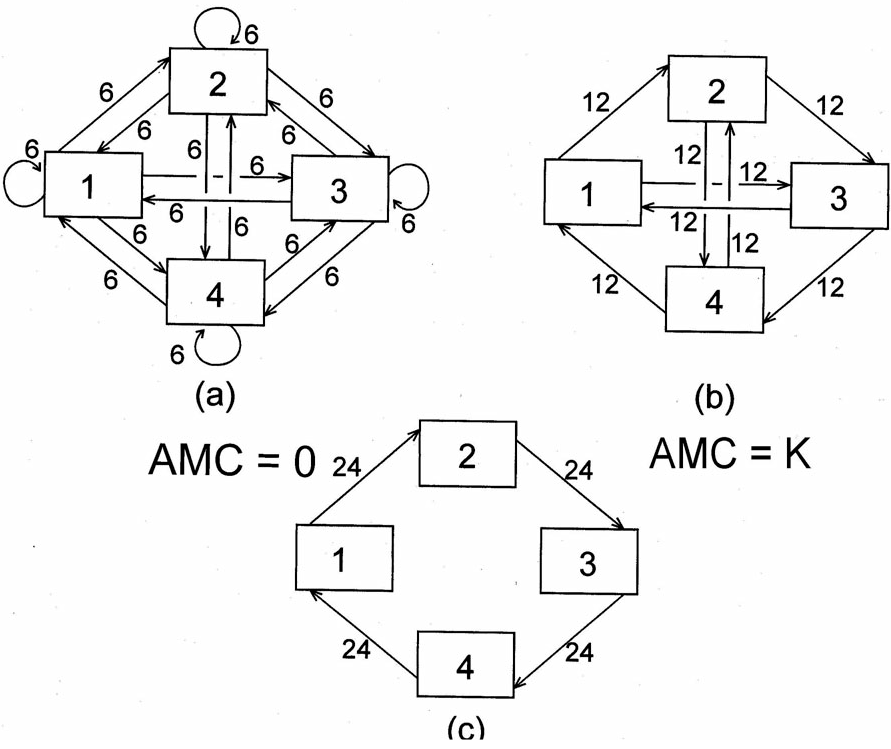
Figure 6 (a) The most equivocal distribution of 96 units of transfer among four system components. (b) A more constrained distribution of the same total flow. (c) The maximally constrained pattern of 96 units of transfer involving all four components
Because autocatalysis is a unitary process that exhibits both the extensive and intensive factors just discussed, we can incorporate the two factors of growth and development into a single index by multiplying them together to define a measure called the system ascendency (Ulanowicz, 1980). In his seminal paper “The strategy of ecosystem development,” Eugene Odum (1969) identified 24 attributes that characterize more mature ecosystems. These can be grouped into categories labeled species richness, dietary specificity, recycling, and containment. All other things being equal, a rise in any of these four attributes also serves to augment the ascendency. It follows as a phenomenological principle that “in the absence of major perturbations, ecosystems have a propensity to increase in ascendency.” Increasing ascendency is a quantitative way of expressing the tendency for those system elements that are in catalytic communication to reinforce each other to the exclusion of nonparticipating members (i.e., quickening).
I should hasten to emphasize in the strongest terms possible that increasing ascendency is only half the story. Ascendency accounts for how efficiently and coherently the system constraints serve to process medium. Again using information theory, one can also compute an index called the system overhead that is complementary to the ascendency (Ulanowicz & Norden, 1990). Overhead (called the “conditional entropy” in information theory) quantifies the degrees of freedom, inefficiencies, and incoherencies present in the system. Although these latter properties may encumber overall system performance at processing medium, they become absolutely essential to system survival whenever the system incurs a novel perturbation. At such time, the overhead becomes the repertoire from which the system can draw to adapt to the new circumstances. Without sufficient overhead, a system is unable to create an effective response to the exigencies of its environment.
It can be demonstrated analytically that the sum of the ascendency and the overhead is proportional to the variety of processes extant in the system. This sum is referred to elsewhere as the system capacity (Ulanowicz & Norden, 1990). That ascendency and overhead are complementary indicates a fundamental tension between the two attributes.
When environmental conditions are not too rigorous (as one might find in a tropical rainforest, for example), then the tendency for ascendency to increase will occur at the expense of overhead. The configurations we observe in nature, therefore, appear to be the results of two antagonistic tendencies (ascendency vs. overhead). Whereas the tendency for ascendency to rise describes the process of development (or quickening), it is constantly being opposed by the opposite (but necessary) tendency (increasing overhead) toward disorder and incoherence (death). It is by analogy to this fundamental tension that one may speak of an ecosystem being the result of a “dialog” between the quick (ascendency) and the dead (overhead).
AN EXPANDED METAPHYSIC
Let us now take stock of the ecological worldview and how it deviates from the conventional assumptions that characterize Newtonian thought. Far more than calling only one or two of the Enlightenment postulates into question, the emerging ecological framework differs from the classical assumptions on each and every point:
- Ecosystems are not causally closed. They appear to be open to the influence of nonmechanical agency. Spontaneous events may occur at any level of the hierarchy at any time, but their domains of influence remain circumscribed by top-down selection processes. Chance does not necessarily unravel a system.
- Ecosystems are not deterministic (dead) machines. They are contingent in nature. Biotic actions resemble propensities more than mechanical forces.
- The realm of ecology is granular, rather than universal. Models of events at any one scale can explain matters at another scale only in inverse proportion to the remoteness between them.
- Ecosystems, like other biotic systems, are not reversible but historical. Irregularities often take the form of discontinuities, which degrade predictability into the future and obscure hindcasting. The effects of past discontinuities are often retained (as memories) in the material and kinetic forms that result from adaptation. Time takes a preferred direction in ecosystems, that of increasing ascendency (quickening).
- Ecosystems are not easily decomposed; they are organic in composition and behavior. Propensities never exist in isolation from other propensities, and communication between them fosters clusters of mutually reinforcing propensities to grow successively more interdependent.
The ecological worldview is not entirely subversive, however. By following Popper's evolutionary leads we have retained some connections with the orthodox and the classical. Because propensities are generalizations of Newtonian forces, it can be shown how the principle of increasing ascendency resembles a generalization of Newtonian law upwards into the macroscopic realm, in a way that resembles how Schrödinger's wave equation was an extension of Newton's second law downwards into the netherworld of quantum phenomena (Ulanowicz, 1999).
LIFE AND DEATH REDUX
In closing we return to the fundamental issues of life and death with which we began this article. In antiquity it was always assumed in one form or another that life preceded the appearance of matter (and death). This belief was displaced by the Enlightenment message that the unchanging (dead) material world (and its attendant eternal laws) preceded any living forms. Physicists and cosmologists, however, have begun to draw a far more dynamical view of the processes that brought our universe into existence. After the initial Big Bang, subtle asymmetries led to the emergence of various enduring forms out of the initial homogeneous substrate, and with them arose the accompanying laws of interaction that are known to us today. Through various feedbacks these forms of matter and their interactions became quite precise and stable, and the physical world as we now know it eventually took shape.
What is notable about this recent cosmological narrative is that the same sorts of processes appeared to be at work during the evolution of the early universe that we have invoked as being active in the development of contemporary ecosystems. Not only do the processes of development appear to antedate the appearance of matter as we know it, but it is also thought by many that ecosystemic feedbacks were already in place to facilitate the appearance of the first identifiable organisms (Odum, 1971). This revised nested sequencing provides an interesting counterpoint to the dilemmas posed by the medieval and Enlightenment extremes. In their places we suggest a phased emergence of one realm from the preceding, all under the modulating influence of the same selection processes. That is, we entertain the sequence {physical {ecological {ontogenetic}}} (Salthe, 1993), where each interior realm emerges from the preceding one according to the same developmental scenario, which imparts ever-higher definition (increasing ascendency) to the successive forms. In this elaboration of forms, some vague precursors of the subsequent stage are thought to exist within the antecedent realm (Salthe, 1993). It should not be assumed, however, that the expression of these predecessors is in any way determinate, because the process of natural creation, like all creative acts, always requires the intervention of at least some contingencies (overhead) (Norton & Ulanowicz, 1992).
We thus come to appreciate how the yawning disparity between dead matter and living forms can be bridged simply by shifting our focus toward the developmental processes that preceded and gave rise to both. In this framework the appearance of life was no more exceptional than was the appearance of matter. The facts that matter became more highly defined before life appeared and that all natural life forms require a material substrate do not imply a superior position for matter in any ontological hierarchy. Hierarchies are predicated on modalities that are selected by those who build them. Most hierarchies are ordered along time and/or space, but one could as well choose organization to define ordinality within a hierarchy (Ulanowicz, 2001). In such an ordering, a howling dog would occupy a higher position than the moon at which it is baying, despite the fact that the moon so vastly exceeds the animal in spatial and temporal extents.
The very practice of ecology forces us to treat the living and the mechanical more evenhandedly, and, by paying close attention to the ongoing “conversation” between the quick and the dead, ecology appears to serve as a very effective interlocutor.
ACKNOWLEDGMENTS
The author was supported in part by the National Science Foundation's Program on Biocomplexity (Contract No. DEB-9981328), the US Environmental Protection Agency's Multiscale Experimental Ecosystem Research Center (MEERC, Contract R819640), and the US Geological Survey Program for Across Trophic Levels Systems Simulation (ATLSS, Contract 1445CA09950093).
References
Capra, F (1975) The Tao of Physics: An Exploration of the Parallels between Modern Physics and Eastern Mysticism, Boston: Shambhala.
Clarke, G.L. (1954) Elements of Ecology, New York: Wiley.
Clements, F E. (1916) Plant Succession: An Analysis of the Development of Vegetation, Washington, DC: Carnegie Institution of Washington.
DeAngelis, D. L., Post, W. M., & Travis, C. C. (1986) Positive Feedback in Natural Systems, New York: Springer-Verlag.
Dennett, D. C. (1995) Darwin's Dangerous Idea: Evolution and the Meanings of Life, New York: Simon and Schuster.
Depwe, D. J. & Weber, B. H. (1994) Darwinism Evolving: Systems Dynamics and the Geneology of Natural Selection, Cambridge, MA: MIT Press.
Eigen, M. (1971) “Selforganization of matter and the evolution of biological macromole- cules,” Naturwiss, 58: 465-523.
Finn, J. T. (1976) “Measures of ecosystem structure and function derived from analysis of flows, Journal of Theoretical Biology, 56: 363-80.
Gibson, J. J. (1979) The Ecological Approach to Visual Perception, Boston: Houghton Mifflin.
Gleason, H. A. (1917) “The structure and development of the plant association,” Bulletin Torrey Botanical Club, 44: 463-81.
Hagen, J. B. (1992) An Entangled Bank: The Origins of Ecosystem Ecology, New Brunswick, Canada: Rutgers University Press.
Haken, H. (1988) Information and Self-Organization, Berlin, Germany: Springer-Verlag.
Haught, J. F. (2001a) “Science, religion, and the origin of life,” AAAS Seminar, Washington, DC, September 13.
Haught, J. F (2001b) God after Darwin: A Theology of Evolution, Boulder, CO: Westview Press.
Huberman, B. A. (ed.) (1988) The Ecology of Computation, Amsterdam: North Holland.
Kauffman, S. (1995) At Home in the Universe: The Search for the Laws of Self-Organization and Complexity, New York: Oxford University Press.
Maturana, H. R. & Varela, F J. (1980) Autopoiesis and Cognition: The Realization of the Living, Dordrecht, Netherlands: D. Reidel.
Norton, B. G. & Ulanowicz, R. E. (1992) “Scale and biodiversity policy: A hierarchical approach,” Ambio, 21: 244-9.
Odum, E. P (1969) “The strategy of ecosystem development,” Science, 164: 262-70.
Odum, H. T. (1960) “Ecological potential and analogue circuits for the ecosystem,” American Scientist, 48: 1-8.
Odum, H. T. (1971) Environment, Power, and Society, New York: Wiley-Interscience.
Patten, B. C. (1999) “Out of the clockworks,” Estuaries, 22(2A): 339-42.
Popper, K. R. (1990) A World of Propensities, Bristol, UK: Thoemmes.
Prigogine, I. & Stengers, I. (1984) Order out of Chaos: Man's New Dialogue with Nature, New York: Bantam.
Sagoff, M. (1997) “Muddle or muddle through? Takings jurisprudence meets the Endangered Species Act,” William and Mary Law Review, 38(3): 825-993.
Salthe, S. N. (1993) Development and Evolution: Complexity and Change in Biology, Cambridge, MA: MIT Press.
Schoener, T. W. (1986) “Mechanistic approaches to ecology: A new reductionsim?,” American Zoologist, 26: 81-106.
Shrader-Frechette, K.S. & McCoy, E. D. (1993) Method in Ecology: Strategies for Conservation, Cambridge, UK: Cambridge University Press.
Simberloff, D. (1980) “A succession of paradigms in ecology: Essentialism to materialism and probabilism,” Synthese, 43: 3-39.
Smuts, J. C. (1926) Holism and Evolution, New York: Macmillan.
Tansley, A. G. (1935) “The use and abuse of vegetational terms and concepts,” Ecology, 16: 284-307.
Ulanowicz, R. E. (1980) “An hypothesis on the development of natural communities,” Journal of Theoretical Biology, 85: 223-45.
Ulanowicz, R. E. (1995) “Utricularia's secret: The advantages of positive feedback in oligotrophic environments,” Ecological Modelling, 79: 49-57.
Ulanowicz, R. E. (1997) Ecology: The Ascendent Perspective, New York: Columbia University Press.
Ulanowicz, R. E. (1999) “Life after Newton: An ecological metaphysic,” BioSystems, 50: 127-42.
Ulanowicz, R. E. (2001) “The organic in ecology,” Ludus Vitalis, 9: 183-204.
Ulanowicz, R. E. & Norden, J. S. (1990) “Symmetrical overhead in flow networks,” International Journal of Systems Science, 1: 429-37.