Handling Complexity with Self-Organizing Fractal Semantic Networks

Jürgen Klenk
IBM, CHE

Gerd Binnig
IBM, CHE

Günter Schmidt
Definiens AG, DEU

Introduction

In today's globally networked world, people are facing dramatically increasing complexity. Part of this complexity is due to the rapidly growing amount of information that is becoming available online. Because knowing more usually leads to better decisions than knowing less (even if the “less” seems clearer and more definite), complex problems require a complex analysis (Davenport & Prusak, 1997), i.e., being aware of the multitude of relevant information available for the decision process, and being able to select the right pieces of information from this multitude. Despite the fact that dealing with complexity is one of the strengths of the human mind, because of the current inflation of information there is a growing need for tools that intelligently assist people in handling complexity.

Current research and state-of-the-art tools for handling complexity are concentrated around topics such as searching and indexing, data mining, classification and clustering, summarization and information extraction, and case-based reasoning, among others. The underlying mathematical models come from disciplines such as statistics, logic, and optimization theory. Depending on the complexity, these methods achieve their tasks with varying degrees of success. In particular, searching on the extremely complex internet is still rather unsatisfactory in many cases due to both low precision and low recall. This is not too surprising, as most tools do not exploit the possibly most important aspect of the human mind when dealing with complexity, the network-like structure of knowledge and thinking.

Network-based approaches (Quillian, 1967) such as neural networks (Müller et al., 1995) and semantic networks (Minsky, 1988a; Reimer, 1991) do concentrate on this aspect. The theory of neural networks even attempts to reinvent the evolution of the brain (in a rather short period). From a scientific point of view, this is certainly an exciting approach. However, we believe that semantic networks provide a more powerful approach for the development of tools that can deal with the exploding complexity of today's world, as they jump into this evolution on a higher semantic level. In this case, the evolving network does not have to reinvent human knowledge and thinking to the extent that these can be built right into the network.

While the network-like structure of knowledge and thinking is one important aspect when dealing with complexity, complexity theory (as originally developed in the biological sciences as a means of understanding how organic entities and communities form) also focuses on the aspect of self-organization. The problem of self-organization itself is extremely complex, because the number of causal factors and the degree of interdependence between them is too great to permit the use of mechanistic prescriptive models to solve it. Instead, self-organization of a complex system is driven on a small (local) scale by a collection of (typically) relatively simple processes, the causal factors. The global outcome very much depends on these local processes and the initial state of the system. Despite the fact that individual local processes are deterministic, the global outcome usually cannot be predicted because the system exhibits chaotic behavior due to its nonlinearity caused by the interdependence of its local processes (Baldi & Politi, 1997).

When combining ideas and theories about self-organization with ideas and theories about knowledge and thinking—that is, when dealing with a self-organizing semantic network—one can model complex problems such as cognition and learning, which relate to the internal state of an entity, as well as the behavior of such entities in communities or collectives, which relate to the external state of the entities. However, in modeling this external state one really deals with self-organizing semantic networks on two different scales, the internal self-organizing semantic network of the community or collective, and those of the entities that make up the collective. This idea can be extended quite naturally to more than two scales. In fact, since most semantic networks typically have a hierarchical structure, all self-organizing semantic networks actually consist of a number of smaller self-organizing semantic networks across different scales.

If one wants to drive the self-organization of the network locally with a few simple processes that are the same on all scales (such as in cellular automata, Gutowitz, 1991), then the network must look the same everywhere, so that these processes can be applied at every location in the network. In other words, the self-organizing semantic network must be self-similar across all scales by being constructed out of a few fundamental building blocks and construction principles. Mathematical objects that are self-similar across hierarchical scales are called fractals, which is why we call the model described in this article a self-organizing fractal semantic network.

DEFINITION OF A SELF-ORGANIZING FRACTAL SEMANTIC NETWORK

We begin with the basic definitions of semantic and hierarchical networks:

It should be noted that this definition does not yield an absolute value for the level of hierarchy, i.e., it does not assign to every node an integer that corresponds to its level of hierarchy. Instead, it gives a relative definition for the level of hierarchy. While this approach is more general, it can cause conflicts because one can have cycles (loops) of hierarchical links. This conflict exists only on a global scale and can be resolved if one considers only local neighborhoods of the whole network at any one time. Local neighborhoods are introduced by the notion of a topology.

In many cases, topological networks are obtained by assigning a weight (a value between 0 and 1) to every link of the network. The negative logarithm of this weight then yields a metric or distance function on the network. The local neighborhoods are defined with the help of some threshold mechanism applied to this metric. Every metric determines a topology, but the converse is not true; therefore, the above definition is more general than the method of assigning weights.

In the special case of semantic networks, it is often required that a semantic unit be used both as a node and as a link. For example, a semantic unit labeled friendship can be viewed both as a node (“friendship is in particular a relation,” where it is a node connected hierarchically to the node relation) and as a link (“friendship between two people,” where it is a link between the two nodes representing the two people). This gives rise to the following definition.

In the next definition we capture what we mean by a fractal network. We will not give an exact mathematical definition (for ideas on how to do this see Edgar, 1990; Mandelbrot, 1982), but rather a working definition, which will suffice for the scope of this article. In particular, our formulation will allow us more easily to define the self-organizing fractal semantic network and to understand the example given in the last section. But this definition will not allow us to explore in more detail the fractal structure of the network. In particular, we will not be able to give a definition for the fractal dimension, which, according to separate studies, seems to be related to the more subjective quantity of complexity. This topic will be covered in a forthcoming paper.

The following definition deals with the processes that perform the selforganization of the network.

For practical purposes, the state of a node or link is often only a function of its local neighborhood. For example, when dealing with semantic networks, a semantic unit is often connected to attributes, and the values of these attributes determine the state of the semantic unit.

It is conceivable that the processes themselves form a hierarchical network. This is a topic under current investigation. The fundamental processes will be covered below.

After making all of the above definitions, we are now in a position to define a self-organizing fractal semantic network, our fundamental model that we use to study complexity problems.

Figure 1 overleaf shows a self-organizing fractal semantic network. Nodes are depicted as spheres, links as cylinders, and processes as Janus heads (see next section for details). The hierarchical structure is clearly visible from the fact that nodes contain internal networks. Note, too, that some links are nodes, as their cylinders have spheres in their center that connect them to other nodes or links.

THE BASIC BUILDING BLOCKS

As specified in definition 1, nodes and links of the network are called semantic units. All semantic units are subdivided into concepts and instances, as is usual (Cohen, 1989). We further subdivide nodes into information units, attribute units, and process units or Janus units. In our model we use the metaphor of a Janus (pl. Jani) for a process. In Roman mythology, Janus is a two-faced god looking in opposite directions, i.e.,

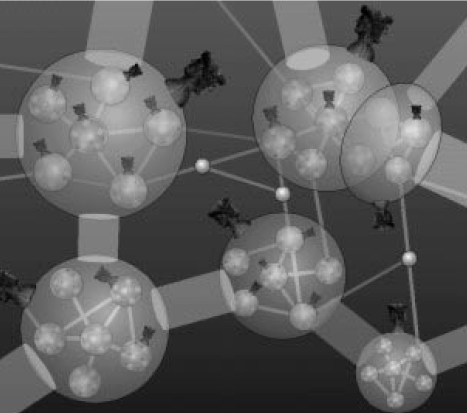
Figure 1 A sample self-organizing fractal semantic network

taking into account a multitude of perspectives. This is exactly what a process in a fractal network does, if one interprets the two directions as the internal, lower-scale and the external, higher-scale parts of the network with respect to the semantic unit to which the process is connected. Information units are general elements that can represent concepts or instances, and they are identified by specific names. Attribute units are identified by specific names and values, which can be set, retrieved, or computed.

All links of the network are either scaling or nonscaling. Standard inheritance principles (Cohen, 1989) are defined across all scaling links, making use of the network's topology or neighborhood concept. Links are further subdivided into comparison units, interaction units, description units, and controller units. Nonscaling comparison units allow us to describe the degree of similarity or dissimilarity of two semantic units, while scaling comparison units allow us to describe how close one semantic unit comes to being an instance of another semantic unit, or how close one semantic unit comes to being a special case of another semantic unit. Nonscaling interaction units allow us to describe the type of interaction of two semantic units, while scaling interaction units allow us to describe the role that one semantic unit plays as part of another semantic unit. Description units connect semantic units to their attribute units, which describe the semantic units in more detail. Finally, controller units connect semantic units to their Janus units, which in turn control and act on the semantic units' local neighborhoods.

Figure 2 shows how the basic building blocks are used to construct a network. Note that each building block labeled “semantic unit” can be replaced with any basic building block. Information units do not appear in this diagram, as there is no restriction on their use. In practice, most of the building blocks labeled “semantic unit” are information units.

In the self-organizing fractal semantic network, each semantic unit has a specific meaning, which it receives indirectly through its multitude

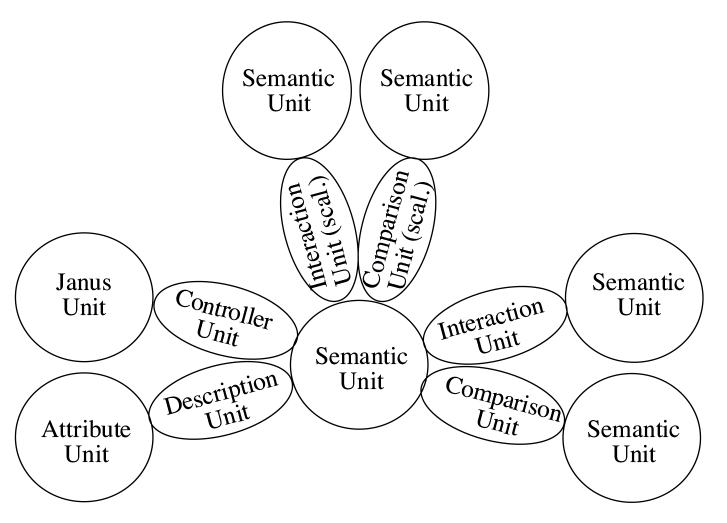
Figure 2 The basic building blocks

of links to other semantic units. Thus, in our model meaning is defined (and is definable) not in an absolute way, but only in a relative way, in accordance with Minsky's philosophy (Minsky, 1988b).

The state of a semantic unit is a (possibly complex) function of all semantic units of its local neighborhood. A simple example is the state of usefulness of the information unit representing a soccer ball. The soccer ball's local neighborhood with respect to the state of its usefulness may consist of the attribute unit size and the attribute unit pressure, together with their respective values. The state of the soccer ball's usefulness can then be computed from the current values of its two attribute units, preferably in terms of fuzzy set theory.

A more complex example is the mood state of a human being. Here clearly, the attribute units describing the human being, such as height and weight, among others, are not sufficient to describe his mood state. Psychologists know that the whole context within which the human being lives affects his mood state. There are many theories about what factors should and should not be taken into account when determining this context, and what kind of influence each of these factors has on the mood state. In our model, it is precisely this context that makes up a human being's local neighborhood with respect to his mood state, and it is precisely the kind of influence each of these factors has that determines the mood state function.

THE BASIC PROCESSES

To motivate the choices for the basic processes in our self-organizing fractal semantic network, we continue with our examples from the last section.

It is important to note that there are Janus units that influence the usefulness of the soccer ball, or the mood state of the human being. Semantic units that are in the local neighborhood of the soccer ball or the human being typically control and trigger these Janus units. If the soccer ball becomes useless because it goes flat (caused by a Janus unit), it may get thrown away (caused by another Janus unit) and thus removed from the network, and a new soccer ball may be purchased (caused by yet another Janus unit), and thus a new information unit representing the new soccer ball is created. As for the human being, he may identify himself as the typical representative of a certain group, and may consequently join this group to improve his mood state, or he may found a new interest group and invite others to join it. To this extent, he may even acquire new skills or knowledge.

These examples illustrate the basic processes required in our model. We have Janus units that are able to create new semantic units, to modify or destroy existing semantic units (and even themselves), to create links between semantic units, to classify or identify semantic units as other semantic units, and to create new groups or segments in the network. Other Janus units must be able to set, retrieve, or compute values of attribute units and to determine the states of semantic units. Finally, there are Janus units that are able to perform a learning task in the form of knowledge acquisition or restructuring.

As can be seen from the Janus units described above, the processes carried out by Janus units can range from generic to specific, meaning that they use generic properties of the basic building blocks that make up the self-similar structure of the network, or very specific properties of the local neighborhood of a certain semantic unit, respectively. Therefore, some Janus units can be connected to any semantic unit, while others require the presence of particular semantic units in the local neighborhood of the semantic unit to which they are connected. Clearly, the Janus units that simply create, modify, or destroy semantic units (including the ones that create links, as this is a special case of creating semantic units) perform very generic tasks. Therefore, they can be connected to any semantic unit. However, they are usually not triggered directly, but rather invoked as parts of more complex processes such as classification or segmentation.

The Janus units that perform the evaluation of attribute units' values typically have a set of mathematical tools at hand from areas such as fuzzy set theory, statistics, geometry, topology, and algebra, among others. Therefore, these Janus units are more specific, as they can be applied only to attribute units whose values satisfy certain type constraints. Finally, the Janus units that determine the states of semantic units are even more specific, as their processes might only be applicable to one or a small group of semantic units.

CLASSIFICATION AND SEGMENTATION

The process of classification stands for the common task of comparing one semantic unit to others. The goal here is to find comparable semantic units in the sense that they are alike, can perform similar tasks, have similar goals, are more general or more specific, are constituents or groups, or are in similar states, among other things. Psychology tells us that this is a very important task, as human beings are constantly in search of their identities by comparing themselves to and (even more importantly) differentiating themselves from others. In our model, the process of classification is performed through extensive local neighborhood analyses. This means that the degree of similarity of two semantic units is determined by the degree of similarity of their local neighborhoods with respect to the above comparison factors. As with determining the status of a semantic unit, when comparing semantic units it is not enough simply to take into account the values of the attribute units of these semantic units. Instead, the topology of the network, i.e., the entire local neighborhood structures of the semantic units, must be considered.

Therefore, the process of classification deals with the more general task of finding similar structures and not just similar values of attribute units. Because of the self-similar structure of the network, this classification process can be implemented in a generic way, thus allowing the Janus unit representing the classification process to be used throughout the entire network.

While classification focuses on finding similar structures among semantic units, segmentation focuses on grouping semantic units according to similarities found during classification. There are two main types of groupings with which our model deals, corresponding to the two types of scaling links we defined, the scaling comparison units and the scaling interaction units. These two types of groupings correspond again to well-known results from psychological studies, people's desire to categorize and organize information and knowledge, and people's desire to form working groups to better achieve a common goal (Wenger, 1998; Prusak & Lesser, 2000). While the categorization and organization of knowledge predominantly use comparing and contrasting mechanisms, working groups are formed according to skills and common goals. Here, it is often the case that diversity is more important than similarity, because working groups are often more successful if they consist of group members with the right mix and variety of skills.

From a process point of view, the results of classification processes determine and trigger segmentation processes. In particular, the classification results determine which new links from semantic units to other semantic units representing categories or groups should be created, and trigger the appropriate segmentation processes that create these links. The classification results also determine which new categories or groups should be created or formed if a number of semantic units have been classified as being similar or having a common goal, and thus should be united/joined/combined/integrated in such new categories or groups. The triggered segmentation processes then create these new categories or groups and also create all links to members of these categories or groups. Again, because of the self-similar structure of the network, this segmentation process can be implemented in a generic way, thus allowing the Janus unit representing the segmentation process to be used throughout the entire network.

Finally, the creation of new semantic units during the segmentation process triggers a new classification process, this time based on the new network structure and topology. This sequence of classification and segmentation, which continuously determines and changes the neighborhood structure and thus influences the states of the semantic units, is the main driver of the self-organization of the network.

AN EXAMPLE

In this section we illustrate how a self-organizing fractal semantic network can be used to model a complex economic and ecological society. Our model is derived from a real-world situation in a rural area in southern Germany and is based on the following assumptions:

  1. A number of farmers are running small agricultural firms. These firms are influenced by standard ecological and economic factors.
  2. Agricultural goods are traded on a market following standard market rules.
  3. There is a dominant (almost monopolistic) market player, a consortium that purchases almost all agricultural products and tries to dictate prices. The consortium performs certain refinement processes, such as making dairy products from milk or running a slaughterhouse.
  4. Farmers have an internal knowledge about producing and selling agricultural goods. Some of the farmers also have a good understanding of the economic situation in marketplaces.
  5. The farmers as well as the consortium are connected to the marketplace. Each has a limited influence on the marketplace, depending on their relative size and importance.
  6. There are consumers of varying size—supermarket chains, butchers, stores, and individuals—purchasing the refined agricultural products.
  7. The goals of the farmers are to maximize their revenue and at the same time to minimize their workload. Their states are determined by the degree of success or failure to achieve their goals.
  8. The goals of the consortium are to maximize its revenue by minimizing the prices for agricultural products, while at the same time ensuring sufficient supply of goods.

When the network evolved out of a given initial state, because of the dominance of the consortium the prices for agricultural goods dropped significantly, causing the farmers' revenues to decrease substantially, despite a similar or even higher workload. As a consequence, the farmers' states changed from satisfactory to unsatisfactory, triggering their classification Jani, which attempted a reclassification of the farmers within the network, based on the new state of the network.

The result of the classification process was that most farmers were in a similar state of dissatisfaction, so that in the subsequent segmentation process a new working group was created within which the farmers organized themselves and shared their knowledge. It was this newly created working group that took over the connection to the marketplace from its individual members. Because of its greater importance, according to the implemented economic rules it could balance the pressure on the prices exercised by the consortium. The prices went up again, giving individual farmers higher revenues and thus greater satisfaction.

One could imagine how this scenario might continue, given that the players have enough information and knowledge at hand to adapt their strategies to the evolution of the network. However, the assumptions made were too simplistic to expect this model to reach a final stable state. Studies based on more refined models are currently under investigation.

CONCLUSIONS

We have shown that aspects of complexity can be modeled with selforganizing fractal semantic networks, where generic processes drive the self-organization of the network on a local scale. Necessary requirements of this model are the existence of a topology or neighborhood structure and the self-similarity of the network on all scales of hierarchy. The two processes of classification and segmentation are fundamental in driving the self-organization of the network, and it appears that cognition and learning can be derived from them. However, more research is necessary to precisely determine the nature of this relation.

Despite the fact that we have given some guidelines on how to extend the concept of fractals from geometry to topological hierarchical networks (definition 5), the question of how to do this in strict mathematical terms is still open. If an answer could be obtained, then it would be interesting to study how the fractal dimension in this network is related to the subjective term of complexity, because this may shed some light on driving mechanisms for learning.

Finally, we have applied the concept of a self-organizing fractal semantic network to the problems of natural language understanding and image recognition. In these cases, texts or images were transformed into initial input networks. Structuring and connecting these input networks to world knowledge networks with the help of the classification and segmentation methods described above then accomplished the task of understanding these texts or images.

NOTE

Gerd Binnig and Günter Schmidt would like to thank the Deutsche Bundesstiftung Umwelt for supporting the simulation project mentioned above.

References

Baldi, R. & Politi, A. (1997) Complexity, Cambridge Nonlinear Science Series 6, Cambridge, UK: Cambridge University Press.

Cohen, G. (1989) Memory in the Real World, Hove, UK: Lawrence Erlbaum Associates.

Davenport, T. H. & Prusak, L. (1997) Working Knowledge, Boston: Harvard Business School Press.

Edgar, G. A. (1990) Measure, Topology, and Fractal Geometry, New York: Springer Verlag.

Gutowitz, H. A. (ed.) (1991) Cellular Automata: Theory and Experiment, Cambridge, MA: MIT Press.

Mandelbrot, B. B. (1982) The Fractal Geometry of Nature, San Francisco: Freeman.

Minsky, M. L. (ed.) (1988a) Semantic Information Processing, Cambridge, MA: MIT Press.

Minsky, M. L. (1988b) The Society of Mind, New York: Simon & Schuster.

Muller, B., Reinhardt, J., & Strickland, M. T. (1995) Neural Networks: An Introduction, 2nd edn, Berlin: Springer Verlag.

Prusak, L. & Lesser, E. (2000) “Communities of practice, social capital, and organizational knowledge,” Knowledge Connections, 2(1, Feb).

Quillian, M. R. (1967) “Word concepts: A theory and simulation of some basic semantic capabilities,” Behavioral Science, 12: 410-30.

Reimer, U. (1991) Einfuhrung in die Wissensreprasentation (”Introduction to Knowledge Representation”), Stuttgart, Germany: B.G. Teubner.

Wenger, E. (1998) Communities of Practice: Learning, Meaning, and Identity, Cambridge, UK: Cambridge University Press.